Печатные шпоры по физике 1 поток от А4-04
.docx|
1. Плоские и сферические волны (без затухания и с затуханием). ГМТ, колеблющихся в одинаковой фазе, называется волновой поверхностью. В простейших случаях они имеют формы плоскости или сферы.Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x,y,z и времени t: ξ= ξ(x,y,z,t)
Упругая волна-процесс распространения возмущений в упругой среде. Продольная волна-волна в которой частицы среды колеблются вдоль направления распространения волны. Фронт волны-ГМТ до которых доходят колебания к моменту времени t. Вид ф. ξ в случае плоской волны: ξ= ξ(x,t) Колебания точек, лежащих в плоскости x=0 (рис.), имеют вид: ξ= ξ(0,t)=acos(ωt+α)
ξ(x,t)=acos[ Введем
величину k=2π/λ= которая называется волновым числом. Уравнение
плоской ,бегущей волны примет вид:
ξ(x,t)=
Уравнение плоской волны при затухании: ξ
= В изотропной и однородной среде волна, порождаемая точечным источником, будет сферической. Уравнение сферической волны: ξ= При затухании: ξ=
|
2. Стоячие волны в струне с двумя закрепленными концами.
|
|
3.Скорость продольных и поперечных упругих волн в тонком стержне. Струна:
В закрепленных концах струны должны
распологаться узлы, поэтому в струне
возбуждаются колебания с условием:
: Эти частоты называются собственными частотами струны. Гармонические колебания с этими частотами называют собственными колебаниями или гармониками. По закону Гука:
Рассмотрим
малый элемент стержня
По 2-ому закону Ньютона:
Запишем
уравнение плоской волны, распространяющейся
вдоль оси
Уравнение для продольных упругих волн в тонком стержне:
Сопоставляя (1) и (2), найдем скорость продольных волн:
где
E-
модуль Юнга,
Уравнение для поперечных упругих волн в тонком стержне:
где
|
4. Связь избыточного давления с интенсивностью звуковой волны в газе. Под интенсивностью понимают среднее по времени значение плотности потока энергии, которую несет с собой звуковая волна.
Т.к.
ξ=acos(
Δ
Т.к.
|
|
5.
Волновое
уравнение для звука в газе. Скорость
звука в газе. Звук
возникает при распространении волн
в упругой среде.(тверд,жидк,газ)
Мгновенное давление в некоторой
точке:
P∆ P∆ P=P’
P’=P/(1+γ( P+∆P=P+Pγ(( P’=P(1-γ(
P P=P’(1+( P’=P/(1+γ(
<Vm>= |
6. Волновое уравнение для продольных упругих волн в тонком стержне.
|
|
7. Колебания струны с двумя закрепленными концами. В
закрепленных концах струны должны
располагаться узлы, поэтому в струне
возбуждаются колебания с условием:
: Эти частоты называются собственными частотами струны. Гармонические колебания с этими частотами называют собственными колебаниями или гармониками.
|
8. Поток энергии в упругой среде. Вектор Умова
Поток
энергии – это количество энергии,
переносимое волной через некоторую
поверхность в единицу времени:
Плотность
потока энергии – это векторная
величина, характеризующая течение
энергии в разных точках пространства:
Интенсивность – модуль среднего по времени значения вектора Умова:
|
|
|
|
|
|
|
|
|
|
|
9.Эффект Доплера для звуковых волн Эффект Доплера – это явление изменения частоты волны, воспринимаемой прибором за счет движения источника либо самого прибора. Положительное направление распространения – от источника к приемнику.
|
12. Энергия электромагнитных волн. Вектор Пойтинга. Плотность энергии электромагнитного поля:
Модуль плотности потока энергии:
Векторы E и H взаимно перпендикулярны и образует с направлением волны правовинтовую систему. Вектор плотности потока энергии (Вектор Пойтинга):
В
случае бегущей гармонической
электромагнитной волны плотность
энергии равна Поток Ф электромагнитной энергии через поверхность σ:
Интенсивность волны:
|
|
10. Плоская монохроматическая электромагнитная волна. Исследуем
плоскую электромагнит волну,
распределенную в нейтральной
непроводящей среде с постоянными ξ
и μ( ρ=0,ϳ=0,ξ=
const,μ=
const)
Направим Ох⊥к
волновым пов-тям. Тогда
|
11. Импульс электромагнитной волны и давление на стенку. Перенос энергии электромагнитной волны сопровождается и переносом импульса. Согласно теории относительности, импульс объекта с нулевой массой покоя, движущегося со скоростью света p=W/c, где W его энергия. Поскольку в случае электромагнитной волны масса покоя «объекта» равна нулю, связь между энергией и импульсом будет такой же: p=w/c, где p и w – плотности импульса и энергии. Умножив числитель и знаменатель на с получим: p=wc/c2 , (wc)- плотность потока энергии, равная по модулю вектору Пойтинга p=[EH]/c2 При полном поглощении телом электромагнитной волны то за промежуток времени dt единице площади поверхности тела сообщается импульс, заключенный в цилиндре с площадью сечения , равной единице, и высотой сdt , т.е. dp=(w/c)cdt. Импульс, сообщаемый единице поверхности в единицу времени , dp/dt , равен давлению p* на поверхность тела. => p* = w , Н/м2
|
|
12. Энергия электромагнитных волн. Вектор Пойтинга. Плотность энергии электромагнитного поля:
Модуль плотности потока энергии:
Вектор плотности потока энергии (Вектор Пойтинга):
Поток
Ф электромагнитной энергии через
поверхность σ:
Интенсивность волны:
|
14. Коэффициенты отражения и пропускания плоской электромагнитной волны. Модули
векторов
Условие
непрерывности тангенсальных
составляющих векторов
Заменяя
векторы
Т.к.
Т.к.
Для
амплитудных значений:
Коэффициент отражения:
Коэффициент пропускания:
|
|
16. Излучение ускоренно движущегося заряда. Мощность дипольного излучения. Мощность излучения Р диполя, т.е. энергия, излучаемая в единицу времени по всем направлениям, пропорциональна квадрату второй производной дипольного момента по времени: Р=(р")2, где =0/6πс или Р=ɷ4(рm)2cos2(ɷt); средняя по времени мощность излучения диполя: <Р>=(/2)ɷ4(рm)2. Средняя мощность излучения осциллирующего диполя зависит от квадрата его амплитуды и очень сильно от частоты. Отсюда следует, что, например, радиостанции должны использовать высокие частоты, а излучение линий передач переменного тока промышленной частоты оказывается незначительным. Формула Р=(р")2 справедлива также для излучения заряда q движущегося ускоренно. Дипольный момент: p=ql=q(r+-r-) где (r+ и r-) радиус-векторы зарядов q и –q. Отсюда: p"=q((r+)"-(r-)")=q(a+-a-) и если заряд q, покоится, а движется только заряд –q, то p"=-qa-, отсюда Pt=q2(at`)2. Это формула для мощности излучения заряда, движущегося с ускорением. Индексы t и t` показывают, что мощность Р в момент t определяется ускорением заряда, которое он имеет в более ранний момент t`=t-l/c (эффект запаздывания). Формула справедлива для зарядов, с малыми скоростями. Заряд, колеблющийся с частотой ɷ, излучает монохроматическую электромагнитную волну с той же частотой ɷ. Если же заряд движется с произвольным ускорением, то его излучение представляет собой спектр различных частот. Заряд, движущийся в вакууме с постоянной скоростью, не излучает. |
18. Векторный потенциал и расчет вектора индукции магнитного поля. В той части пространства, где плотность тока не равна нулю (правая часть уравнения rot(H)=J не равна нулю), магнитное поле можно рассматривать как вихревое. В этом случае вектор магнитной индукции можно представить в виде вихря некоторого вспомогательного вектора A: B=rotA, вектор А носит название векторного потенциала магнитного поля. Единицей измерения для векторного потенциала является (Вб/м)=(В*с/м). Основанием для представления индукции в виде B=rotA служит то, что при этом всегда соблюдается закон непрерывности магнитного потока divB=0. В однородной среде для векторного потенциала справедливо уравнение Пуассона: 2A=-J и, в частности, уравнение Лапласа: 2A=0. Общее решение уравнения может быть представлено в следующем виде: A=(/4π)*∫v(J/r)dv. Интегрирование достаточно распространить по всему объему, где плотность тока J≠0. Величина r - расстояние от центра элемента объема dv, в котором плотность тока равна J до точки, в которой определяется A. Данное выражение для определения вектора A по заданному распределению тока в пространстве справедливо всюду, в частности и там, где вектор J=0. Выражение A=(/4π)*∫v(J/r)dv может быть упрощено, если токи протекают по контурам из линейных проводников, поперечные размеры сечений которых весьма малы по сравнению с длиной контуров и с расстоянием от проводников до точек, в которых определяется вектор А. В этом случае формулу можно преобразовать к виду: A=(/4π)*∫l(i/r)dl. Закон Био-Савара-Лапласа и принцип суперпозиции позволяют рассчитать индукцию магнитного поля B, создаваемого произвольной системой электрических токов, в произвольной точке пространства. Для этого необходимо разбить все токи на бесконечно малые участки (I∆l)k, записать выражения для векторов для индукции поля (∆B)k, создаваемых этими элементами (пользуясь законом Био-Савара-Лапласа) и просуммировать полученные выражения (что позволяет принцип суперпозиции) для всех участков тока B=Σk(∆B)k. Рассмотрим участок проводника с током. Выражение для элемента тока I∆l записывается также в виде I∆l=jS∆l= j∆V. В том случае, когда электрические токи не являются линейными, а пространственно распределенными (то есть текут не только по тонким проводам), выражение для элемента тока I∆l следует заменить эквивалентным j∆V и провести суммирование по всем элементам объема, где протекают электрические токи. |
|
20. Понятие о световом луче. Оптическая длина пути. Световой луч — это геометрическая линия, которая в каждой своей точке перпендикулярна волновому фронту, проходящему через эту точку. Направление светового луча совпадает с направлением распространения света. Основу геометрической оптики составляют три закона: 1) закон прямолинейного распространения света (в однородной среде). Этот закон приближённый, так как, например, при прохождении через малые отверстия наблюдается отклонение от прямолинейности. 2) Закон независимости световых лучей: «лучи при пересечении не возмущают друг друга». Он справедлив при не слишком больших интенсивностях. 3) закон отражения света: угол отражения света равен углу его падения, и оба луча лежат в одной плоскости с нормалью к поверхности раздела, её называют плоскостью падения. 4)Закон преломления света: при преломлении света на границе раздела двух изотропных сред с показателями преломления n1 и n2 выполняется условие: n1sin=n2sin. Отсюда, в частности, следует, что при падении света на оптически менее плотную среду (n2<n1) угол может достигнуть 90 градусов. Соответствующий угол падения называют предельным: sinпред=n2/n1. Для углов падения >пред наблюдается полное внутреннее отражение. Это явление нашло достаточно широкое практическое применение. Оптическая длина пути, оптический путь, между точками А и В прозрачной среды; расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения от А до В. Поскольку скорость света в любой среде меньше его скорости в вакууме, оптическая длина пути всегда больше реально проходимого светом расстояния (или, в предельном случае вакуума, равна ему). В оптической системе, состоящей из р однородных сред (траектория луча света в такой системе – ломаная линия), оптическая длина пути равна сумме Σlknk где lk - расстояние, пройденное светом в k-йсреде (k - 1, 2,..,), nk - показатель преломления этой среды. В среде с плавно меняющимся п(1)(траектория луча в такой среде - кривая линия) оптическая длина пути есть А∫Вn(l)dl, где dl - бесконечно малый элемент траектории луча. Понятие “оптическая длина пути” играет большую роль в оптике, особенно в геометрической оптике и кристаллооптике, позволяя сопоставлять пути, проходимые светом в средах, в которых скорости его распространения различны. Геометрическое место точек, для которых оптическая длина пути, отсчитываемая от одного источника, одинакова, наз. поверхностью световой волны; световые колебания на этой поверхности находятся в одинаковой фазе. Оптическая длина пути луча света между двумя произвольными точками пространства предметов и пространства изображений называется эйконалом. |
21. Принцип Ферма. Законы отражения и преломления. Принцип Ферма утверждает: свет распространяется по такому пути, оптическая длина которого минимальна. Точнее, оптическая длина пути должна быть экстремальной, т.е. либо минимальной, либо максимальной, либо стационарной – одинаковой для всех возможных путей. В последнем случае все пути света между двумя точками оказываются согласно таутохронными. Воптически однородном веществе свет распространяется прямолинейно, но на границах раздела сред – отражается и преломляется и его путь становится ломаным. В неоднородной среде, где показатель преломления непрерывно меняется, лучи света являются кривыми линиями. Если не рассматривать дифракцию, то распространение светового луча описывается общим принципом, носящим название принцип Ферма. Сам Ферма сформулировал свой принцип в 1679 году так. Свет при распространении от одной точки к другой выбирает путь, которому соответствует наименьшее время распространения. При этом Ферма руководствовался теологическими соображениями: природа действует целенаправленно; она не может быть расточительной и должна достигать своих целей с наименьшей затратой средств.. Эти соображения, конечно, не могут служить объяснением, но сам принцип в основнои верен, требует только некоторых уточнений. Выразим принцип Ферма количественно. Для этого введем оптическую длину пути l=ns, а в случае неоднородной среды – dl=nds, где s – геометрический путь луча, ds – его малый отрезок, n– показатель преломления среды. Таким образом, оптическая длина пути из точки А в точку В выражается криволинейным интегралом l=A∫Bnds. Свет распространяется по пути, оптическая длина которого экстремальна, т.е. она является либо минимальной из всех возможных, либо максимальной, либо стационарной. Условие экстремальности сводится к требованию, чтобы вариация этого интеграла равнялась нулю: δА∫Вnds=0. Это и есть математическая формулировка принципа Ферма. Принцип Ферма может быть получен из волновой оптики (там речь идет о нормалях к фронту волны) и может быть строго доказан. Из принципа Ферма следуют все три закона геоиетрической оптики для распространения света. Также из него следует закон обратимости: если свет распространяется из А в В по некоторому пути, то из В в А он будет распространяться по тому же пути. Рассмотрим некоторые частные случаи. |
|
В случае гармонической волны эта величина пульсирует с достаточно большой частотой и интерес представляет лишь её среднее значение по времени: p*=<w> Для идеально отражающей поверхности давление будет в 2 раза больше. p*=<w>(1+R)
, R
– коэффициент отражения (отношение
интенсивности отраженной волны к
интенсивности падающей)
*
Электрическое поле волны возбуждает
в теле ток плотности j=
Fед=
[jB]=
|
Если
было создано поле
для
того чтобы уравнения удовлетворялись
необход α1=α2. Кроме того
|
|
15. Излучение дипольного осциллятора. Диаграмма направленности. Возбуждение
электромагнитных волн какой-либо
системой называют излучением этих
волн, а саму систему – излучающей
системой. Поле электромагнитной волны
называют полем излучения. Электромагнитные
волны в вакууме возбуждаются
электрическими зарядами, движущимися
с ускорением. Простейшей излучающей
системой является осциллирующий
электрический диполь, момент
р которого
изменяется с течением времени, –
элементарный
вибратор.
Если излучающая система электронейтральна,
а ее размеры малы по сравнению с длиной
ℷ
излучаемых волн, то в точках, отстоящих
от системы на расстоянии r>>ℷ
- в волновой зоне – поле излучения
близко к полю излучения осциллятора,
имеющего такой же электрический
момент, как и вся излучающая система.
Закономерности излучения линейного
гармонического осциллятора
электрического диполя, размер которого
l<<ℷ,
p=-qr=-qlercos(ɷt)=pmcos(ɷt);
в вакууме: ℷ=2πc/ɷ.
В непосредственной близости от диполя
картина электромагнитного поля очень
сложна. В волновой зоне: быстро
спадающее статическое поле практически
исчезает и остается только поле
излучения от осциллирующих зарядов
– расходящаяся сферическая волна с
той же частотой, что и у осциллятора.
Амплитуда волны: Em~Hm~(1/r)sinɵ,
ɵ-угол между осью диполя и радиус-вектором
r
точки, где наблюдается поле. Вектор
Е
в каждой точке волновой зоны направлен
по касательной к меридиану, а вектор
Н
– по касательной к параллели, в каждый
момент Е
и Н
составляют правую тройку с вектором
Пойнтинга П=[EH].
Интенсивность электромагнитной
волны, т.е. среднее значение плотности
потока энергии <П>, пропорционально
произведению EmHm,
значит: I=<П>~(1/(r2))sin2(ɵ).
Зависимость I(ɵ)
наглядно изображают с помощью диаграммы
направленности
излучения диполя. Здесь длина отрезка
ОО’, отсекаемого на луче под углом
ɵ, дает интенсивность излучения под
этим углом. Видно, что максимум
излучения происходит в экваториальной
плоскости (ɵ=π/2),
а вдоль оси (ɵ=0) диполь не излучает
совсем. |
13. Волновое уравнение для электромагнитных волн в однородном изотропном диэлектрике. Скорость электромагнитных волн Для
однородной нейтральной
Возьмем
ротор
Аналогично можно получить
Это и
есть волновые ур-ния для электромагнитной
волны, где
|
|
19. Эффект запаздывания и расчет вектора Умова-Пойтинга для дипольного излучения. Рассмотрим заряженную частицу, которая покоится в начале координат. В момент времени t1 частица начала движение и остановилась в точке x2 в момент времени t2. До начала движения линии равного потенциала представляли собой семейство сфер, имеющих общий центр. Поскольку потенциал заряда описывается неоднородным волновым уравнением, решение задачи выражается через запаздывающие потенциалы. Для небольших скоростей потенциал точечного заряда хорошо описывается потенциалами Лиенара-Виехерта ф=q/(4πε(R-vR/c)). Запаздывающим этот потенциал называется потому, что при движении заряда он не меняется сразу (одновременно) во всем пространстве. Изменение потенциала происходит спустя некоторое время после изменения положения заряда. Это время зависит от расстояния между точкой наблюдения и зарядом и равно отношению этого расстояния к скорости света. За счет этого запаздывания изменения потенциала информация о перемещении заряда «записывается» в пространстве подобно тому, как звук записывается на движущейся магнитофонной ленте. В обычной изотропной среде с проницаемостью ε и плотность энергии электромагнитного поля равна сумме плотностей энергии электрического и магнитного полей: w=εε0E2/2 +0H2/2. Плотность электрической энергии в бегущей волне равна плотности магнитной энергии: w= εε0E2=(εε00)1/2EH=EH/v. Умножив w и v, получим плотность потока энергии: П=wv=EH. Векторы Е и Н взаимно ортогональны и образуют с направлением распространения волны правовинтовую систему. Значит, направление вектора [EH] совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН. Поэтому ветор плотности потока электромагнитной энергии П можно представить как: П=[EH]. Вектор П называют вектором Пойтинга.
|
17.
Эффект Доплера для электромагнитных
волн. 1) Доплеровское смещение частоты электромагнитных волн определяется только скоростью источника относительно приемника. Пусть в системе отсчета К находится неподвижный приемник Р. К нему с релятивистской скоростью V приближается источник периодических электромагнитных сигналов S. В системе отсчета К`, связанной с источником, сигналы испускаются с частотой ν0 (собственная частота). Найдем частоту ν, с которой воспринимаются эти сигналы приемником. Промежуток времени между двумя последовательными сигналами в К`-системе, связанной с источником, равен Т0=1/ν0. Источник движется со скоростью V, поэтому промежуток времени в К-системе, согласно «эффекту замедления хода движущихся часов» будет больше: Т=Т0/(1-2)^(1/2), =V/c, ℷ=сТ-VT=(c-V)T0/(1-2)^(1/2). Поэтому ν=с/λ=ν0(1-2)^(1/2)/(1-V/c). Если источник приближается, то ν>ν0, если же удаляется, то ν<ν0 (в этом случае знак перед V меняется на противоположный). Полученная формула соответствует продольному эффекту Доплера. Эффект Доплера для электромагнитных волн является следствием двух явлений: замедление хода движущихся часов и «уплотнения» импульсов, связанного с изменением расстояния между источником и приемником. 2) В К-системе источник S движется со скоростью V, составляющей угол с линией наблюдения. Следовательно, Vx=Vcos, тогда ν=ν0(1-2)^(1/2)/(1-Vx/c). В процессе движения источника S проекция скорости меняется, поэтому необходимо учесть эффект запаздывания. Воспринимаемая приемником Р частота ν в момент t будет обусловлена сигналами, испущенными источником S в предшествующий момент t`=t-l/c, где l – расстояние от источника S до приемника P в момент t`. Поэтому значение Vx надо брать в момент t`. При =90 наблюдается поперечный эффект Доплера: ν=ν0(1-2)^(1/2), при котором воспринимаемая приемником частота оказывается всегда меньше собственной частоты источника. Поперечный эффект является прямым следствием замедления хода движущихся часов. Этот эффект значительно слабее продольного. В нерелятивистском случае, когда V<<c, можно считать, что T=T0, и тогда воспринимаемая частота ν= ν0/(1-Vx/c). Отсюда относительное изменение частоты (ν-ν0)/ν0
равно
|
|
1) Прямолинейное распространение света в однородной среде очевидно.2) Отражение от плоской поверхности. 3)Преломление на плоской поверхности раздела двух сред. Точно так же, если посчитать путь преломленного луча и найти его минимум, получим закон преломления. 4) Пример стационарности хода луча – прохождение лучей через линзу. Лучи проходят так, что все пути лучей таутохронные – там, где линза тоньше геометрический путь длиннее. 5) Миражи. Законы отражения и преломления: возможность видеть несветящиеся предметы связана с тем обстоятельством, что всякое тело частично отражает, а частично пропускает или поглощает падающий на него свет. Благодаря явлению диффузного отражения и пропускания, свет, падающий на тело, рассеивается в разные стороны, и мы получаем возможность видеть тело с любой стороны. Для того чтобы имело место зеркальное отражение или преломление, поверхность тела должна быть достаточно гладкой (не матовой), а его внутренняя структура — достаточно однородной (не мутной). Это означает, что неровности поверхности, равно как и неоднородности внутреннего строения, должны быть достаточно малы. Для того чтобы поверхность была оптически гладкой, а тело оптически однородным, необходимо, чтобы неровности и неоднородности были значительно меньше микрометра. Рассмотрим вначале отраженные лучи. Накроем поверхность раздела (зеркало) сверху непрозрачной цилиндрической поверхностью АСВ. На дуге АСВ проделаем небольшие отверстия, расположенные, например, через каждые 5⁰. Тогда окажется, что если луч света пропущен в одно из этих отверстий и направлен по радиусу дуги АСВ к центру О, то после отражения он выйдет из прибора через симметричное относительно перпендикуляра NO отверстие в цилиндрическом колпаке, покрывающем зеркало. Этот надежно установленный результат можно формулировать в виде следующего закона отражения света: луч падающий, луч отраженный и перпендикуляр к отражающей поверхности лежат в одной плоскости, причем угол отражения луча равен углу падения. Измерение угла, образуемого преломленным лучом с перпендикуляром к поверхности раздела (угла преломления), можно проделать тем же способом, какой мы использовали при измерении угла отражения. Для этого нужно продолжить цилиндрическую поверхность АСВ во вторую среду. Точные измерения угла падения и угла преломления приводят к следующему закону преломления: луч падающий, луч преломленный и перпендикуляр к поверхности раздела лежат в одной плоскости. Угол падения и угол преломления связаны соотношением: sin/sin=n1/n2.
|
|
|
22. Кривая относительной спектральной чувствительности глаза. Поток энергии и световой поток. Распределение
потока энергии по длинам волн можно
охарактеризовать с помощью функции
распределения
|
23. Сила света и освещенность. Фотометрия - раздел оптики, занимающийся измерением световых потоков и величин, связанных с такими потоками. Сила света. Источник света, размерами которого можно пренебречь по сравн. с расст. от места наблюдения до источника, наз. точечным. В однор. и изотропной среде волна, излучаемая точечным источ., будет сферической. Для хар-ки точечных источн. света примен. сила света I (поток излучения источника, приходящийся на единицу телесного угла):
направлениям.
Освещенность.
Степень освещенности некоторой
поверхности падающим на нее светом
характеризуется величиной
|
|
24. Светимость и яркость. Ламбертовский источник. Протяженный
источник света можно охарактеризовать
светимостью
М
различ.
его участков, под кот. понимается
световой поток, испускаемый единицей
площади наружу по всем направлениям
(в пределах значений
Светимость
может возникнуть за счет отражения
пов-тью падающею на нее света. Тогда
под Светимость
хар-ет излучение (или отражение) света
данным местом поверхности по всем
напр. Для хар-ки излучения (отражения)
света в заданном направлении служит
яркость
L
(отношение силы света элементарной
пов-ти
|
25.Кардинальные точки и плоскости центрированной оптической системы. Формула Ньютона. Оптическая система - совокупность отражающий и преломляющих пов-тей, отделяющих друг от друга оптически однородные среды. Обычно эти пов-ти бывают сферич. или плоск. (пл-ть можно рассматривать как сферу бесконеч. радиуса). Оптическая сист., образованная сферическими (в частности, плоскими) пов-тями, наз. центрированной, если центры всех пов-тей лежат на одной прямой. Эту прямую наз. оптической осью системы. Каждой
точке Р пли пл-ти S
в пр-ве предметов соотв сопряженная
с ней точка Р' или плоскость S'
в пр-ве изображений. Среди бесконечного
мн-ва сопряженных точек и сопряженных
пл-тей имеются точки и пл-ти, обладающие
особыми св-вами. Такие точки и пл-ти
наз. кардинальными.
К их числу относятся фокальные,
главные и узловые точки и пл-ти. Задней
фокальной пл-тью F'
наз.
пл-ть, сопряженная с находящемся
на бесконечности в пр-ве предметов
пл-тью
Точка пересеч.задней фок. пл-ти с оптич. осью наз. задним фокусом системы. Передней фок. пл-тью F явл. пл-ть, сопряженная с находящейся на бесконечности в пр-ве изображений пл-тью S’’ перпендикулярной к оси системы.. Точка
пересеч. передней фокальной пл-ти
F
с оптической осью наз. передним фокусом
системы.
|
|
26. Формула тонкой линзы. Оптическая сила линзы. Простейшей центрированной оптич. системой явл. линза (прозрачное (обычно стеклянное) тело, ограниченное 2 сферич. пов-тями). Точки пересечения пов-тей с оптич. осью линзы наз. вершинами преломляющих пов-тей. Расстояние между вершинами наз. толщиной линзы, Если толщиной линзы можно пренебречь по сравнению с меньшим из радиусов кривизны ограничивающих линзу пов-тей, линза наз. тонкой. Ф-ла тонкой линзы:
|
28.
Интерференция плоских волн.
При
наложении двух пучков света с
интенсивностями I1 и I2 распределение
интенсивности в интерференционной
картине описывается формулой: I=
I1
+ I2
+2√
I1 I2
cos
k
|
|
30. Временная когерентность, длина когерентности на примере опыта Юнга.
Когерентность-согласованное
протекание колебательных(волновых)процессов.Степень
согласованности-степень когерентности. Опыт Юнга: S-узкая щель,освещенная ярким пучком солнеч.света, S1 и S2 -узкие щели,вторичные когерентные источники, исходящие из них волны дают на экране Э интерф. картину,которая по мере удаления от ее середины размывается.Полосы исчезают при m˃x порядка интер-ии,т.е. пока разность хода ∆ ≤ xλ,колебания когерентны.Интервал равный xλ называют длиной когерентности lког (lког ≈ mλ, m-макс.порядок интер-ии,соотв-ий еще видимой светлой полосе). Реальный свет немонохроматичен,он представляет собой последовательность отдельных цугов волн различной частоты(длины),в некотором конечном интервале длин волн (λ, λ+∆λ). Ширина интер-ой полосы(расстояние между соседними max) ∆x= λ*l / d, ∆x ~ λ.
Сплошные
отрезки-положения максимумов для λ,
пунктирные-для λ+∆λ.Максимумы
промежуточных длин волн-штриховка.Промежуточные
max
постепенно заполняют интервал между
max
соседних порядков для λ и
λ+∆λ.Результирующие максимумы(нижняя
часть рис.)будут постепенно размываться,
и полосы интер-ии исчезнут.Из рис.при
m(λ+∆λ)
≈ (m+1)λ,
m-предельный
порядок инт-ии,m≈
λ/∆λ. λ/∆λ- степень монохром.света:чем
больше,тем больше и ст.монохром-ти.
lког
≈
mλ,
lког≈
λ2/∆λ.
Для
получения интер-ой картины необходимо
lког
˃∆.
Время когерентности τког-промежуток
времени,в течение которого случайные
изменения фазы свет.волны в данной
точке достигает значения порядка π.
lког
=сτког
|
32.Интерферометр Майкельсона.
Пучок
света от S
падает на полупрозр.пластину Р1,покрытую
тонким слоем серебра. ½ светого потока
от Р1
отражается в направлении луча 1, ½
проходит сквозь пластинку в напр.
луча 2. Пучок 1 отражается от зеркала
М1
и
возвр-ся к Р1,где
делится на 2 равных по интенс-ти
пучка.Один из них проходит сквозь Р1
и образует 1’,второй отраж-ся в напр-ии
к S.Пучок
2,отразившись от М2,возвр-ся
к Р1,где
делится на две части:отразившийся от
Р1
пучок
2’ и прошедший через Р1.Пучки
1’ и 2’ имеют одинаковую нтенсивность.При
соблюдении врем. И простран. когерентности
они будут интерф-ть.Луч 2 проходит
пластинки трижды,луч 1-один раз.Чтоб
скомпенсировать разную для различных
длин волн оптич.∆,на пути 1 ставится
тонкая пластинка Р2.Интерф.картина
наблюдается через трубы Т. М2’
– мнимое изображение М2
в
Р1.Тогда
рассматриваем 1’ и 2’ как возникшие
за счет отражения от прозрачной
пластинки,ограниченной М1
и
М2’.
Винт W1
изменяет
угол между М1
и
М2’,можно
установить строго параллельно.W2
перемещает
М2
не
изменяя его наклона.Можно заставить
М1
и
М2’
пересечься.
1.Пучок параллелен,угол
между М1
и
М2’не
равен нулю. Наблюдаем полосы равной
толщины,они парал-ны линии
пересеч.плоскостей М1
и
М2’.В
белом свете все полосы окрашены,кроме
той,что совпадает с линией
пересечения(нулевая полоса)-она
черная(т.к. между лучом 1 и 2 разность
фаз равна π)
2.При расходящемся свете
и строго парал плоскостях М1
и
М2’
–полосы равного наклона(кольца,их
радиус изменяет винт W2).Смещение
картины на 1 полосу соотв.перемещению
зеркала М2
на половину длины волны.
|
|
|
По
гориз. оси отложена длина волны
|
|
Перпендикулярные
к оси пл-ти, проходящие через узлы,
наз. узловыми пл-тями (передней и
задней).
|
Источники,
яркость которых одинакова по всем
направлениям (L=const),
наз. ламбертовскими
(подчиняющимися закону Ламберта) или
косинусными (поток, посылаемый
элементом пов-ти такого источника,
пропорционален
Разделив
на
|
|
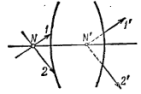
29.
Пространственная когерентность,радиус
когер. на примере опыта Юнга.
S-не
узкая щель,состоящая из бесконечно
узких щелей.Сплошные отрезки-максимумы
от точки 1,пунктирные-от точки
2,штриховка-промежуточные max
между 1 и 2. При расширении S
расстояния между максимумами 1 и 2
будут ув-ся и интервалы между соседними
max
от одного края щели будут заполняться
максимумами от ост эл-ов щели. Пусть
а=b.
При s=∆x
интервал между соседними max
от 1 будет заполнен максимумами от
ост эл-ов щели,интерф-ые полосы
исчезнут.
Интерф-ая
картина исчезает, потому что щели S1
и
S2
становятся
некогерентными.
Ширина(радиус)пространственной
когерентности hког
-характерное
для данной установки расстояние между
точками пов-ти,перпендикулярной
направлению распростр волны.( между
S1
и
S2) hког≈ d=, d-расстояние между S1 и S2, известно s=∆x, ∆x= λ*l / d,отсюда hког≈d= λ*l /∆x ≈ λ*l / s= λ/(s/l) =λ/φ, φ-угловая ширина щели S относительно диафрагмы с двумя щелями.hког ≈ λ/φ d= λ/φ Для получения интер-ой картины необходимо hког ˃ d
|
27. Явление интерференции. Сложение двух электромагнитных волн. Интенсивность суммарной волны. Пусть
2 волны одинаковой частоты, накладываясь
друг на друга, возбуждают в некот.
точке пр-ва колебания одинакового
направления:
При наложении когерентных световых волн происходит перераспределение светового потока в пр-тве, в результате чего в одних местах возникают максимумы, а в других — минимумы интенсивности. Это явл. наз. интерференцией волн. |
|
|
31. Способы наблюдения интерференции света.Бизеркала(или бипризма)Френеля.
Зеркала.
угол α очень мал. зеркала отбрасывают
на экран Е две ког.волны так,как если
бы они исходили из мнимых источников
S1
и
S2.
Непрозр.экран Е1
преграждает свету путь от источника
S
к экрану Е.Луч ОQ-отражение
SO
от ОМ, луч ОР - от ОN.
d=2r
sinα
≈ 2rα
a=r
cosα
≈ r
l=r+b,
b-расстояние
от линии пересеч зеркал до Е
∆x=
λ*l
/d
∆x=
Бипризма. n-показатель преломления призмы ϑ-малый преломляющий угол призмы α=(n-1)ϑ d=2a sinα ≈ 2aα=2a(n-1)ϑ
l=a+b
∆x= λ*l
/d ∆x=(a+b)λ/ 2a(n-1)ϑ
область
перекрытия
PQ имеет
протяженность
2b
tgα
≈ 2bα=2b(n-1)ϑ
N=4ab(n-1)2ϑ2
/ λ(a+b)
|
|
33.
Интерференция света на тонких пленках.
Просветление оптики.
∆=ns2
– s1
оптич.разность
ходаs1
=OA
s2=OC+CB,
пусть nокр.среды=1
s1=2b
tgi2
sin(i1)
s2=2b/cos(i2) ∆=2bn / cos(i2) - 2b tgi2 sin(i1) n sin(i2)= sin(i1) n cos(i2)=√( n2 - sin2(i2) n2)=√ n2-sin2(i1) ∆=2b√( n2-sin2(i1) ) Возможно ∆=2b√( n2-sin2(i1) ) – λ0/2, если луча от более плотной среды, λ0-длина волны в вакууме. Эти волны смогут интерферировать, если будут соблюдены усл как временной,так и простран. когерентности. |
34.Интерференционные полосы равной толщины.
Пластинка
в виде клина с углом при вершине
φ.Падает парал.пучок лучей,отраженные
-не параллельны. Направления
распространения волн, отраженных от
верхней и нижн. пов-ти клина, не
совпадают.Допустим,что временная и
простр когерентности выполняются:
lког
˃∆
и hког
˃
d=длина
клина.Тогда отраженные волны будут
когерентными всюду и на экране будут
инер. полосы.При ограниченной
пространств.когерентности область
пространства,располагая в кот
экран,можно будет увидеть
интерф.картину,тоже будет ограниченной.Если
расположить экран так,как экран Э, то
на нем возникнет интерф.картина даже
если пространств.когерентность
падающей волны крайне мала(в Q’
и Q”
пересек лучи,которые до падения на
клин совпали -это при малом φ разность
хода можно вычислить по ф-ле: ∆=2b√(
n2-sin2(ϑ1)
) – λ0/2,беря
в кач-ве b
толщину пластинки в месте падения
лучей.Т.к. ∆ для лучей на различных
участках клина неодинакова – на
экране появятся светлые и темные
полосы. Каждая из таких полос возникает
в результате отражения от участков
клина с одинаковой толщиной, их
называют полосами равной толщины.По
мере приближения к вершине клина
становятся более благоприят. условия
для врем. и простр. ког-ти. Отчетливость
интерф. картины ум-ся при перемещении
к основанию клина.
|
|
36. Формула Ньютона. Кольца Ньютона.
|
|
|
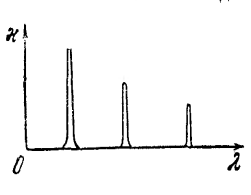
37. Многолучевая интерференция. Явление
интерференции применяют на практике
для изучения характеристик оптического
излучения – анализа структуры
светового поля, измерения спектра и
т. п. При этом для увеличения резкости
интерференционной картины часто
используют принцип многолучевой
интерференции, когда в образовании
интерференционного поля участвуют
несколько световых лучей. Основные
особенности многолучевой интерференции
можно рассмотреть с помощью прозрачной
плоскопараллельной пластинки.
Предположим, что плоская монохроматическая
световая волна падает на плоскопараллельную
стеклянную пластинку, обе грани
которой хорошо отражают свет (рис.
5.5). Частично проникая в пластинку,
свет многократно отражается от ее
граней. При каждом отражении часть
излучения выходит наружу, образуя
набор плоских волн, которые интерферируют
между собой. Коэффициент пропускания
такой пластинки определяется
выражением
|
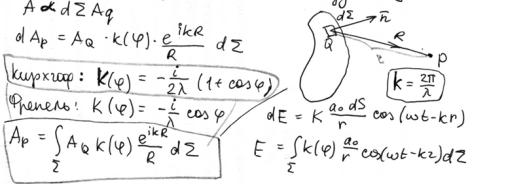
38. Принцип Гюйгенса-Френеля. Интеграл Кирхгофа и его представление в виде ряда. Поведение света за преградой можно объяснить с помощью принципе Гюйгенса: Каждая точка , до которой доходит волна , является источником вторичных волн , а огибающая этих вторичных волн дает положение фронта волны в следующий момент.Принцип Гюйгенса-Френеля : для определения колебания в точке Р , лежащей перед некоторой поверхностью S , надо найти колебания , приходящие в эту точку от всех элементов dS поверхности S и затем сложить их с учетом амплитуд и фаз.
См. обратную сторону
Теорема Бабине. Эта теорема касается свойств дополнительных экранов. Эта теорема следует из того , что согласно принципу Гюйгенса-Френеля волны можно представить как сумму вторичных волн , исходящих из каждого элемента площади отверстий экрана.
|
|
39. Графическое сложение амплитуд. Зоны Френеля.
Воспользовавшись
данным радиусом , разобьем поверхность
на кольцевые зоны , причем так , чтобы
расстояние от краев каждый зоны до
точки Р различались на
|
40. Дифракция Френеля на круглом отверстии и на диске. Сферическая
волна , распростр. Из точечного
источника S
, встречает на пути экран с круглым
отверстием. Экран плоскости отверстия
находится от него на расстоянии b.
Разобьем откр. часть волновой
поверхности на зоны Френеля. Когда отверстие откр. нечетное число зон Френеля , то амплитуда (интенсивность) в т. P будет больше , чем при своб. Распространение волны. Если четное , то A(I) будет = 0. Если отверстие откр. одну зоны Френеля , то в т. P A=A1 т.е. вдвое больше , чем в отсутствие непрозрачного экрана с отверстием. Интенсивность соотв. Больше в 4 раза. Таким образом , дифр. картина от круглого отверстия будет иметь вид чередующихся темных и светлых колец с центрами в т.P. |
|
35. Интерференционные полосы равного наклона. Плоскопараллельная пластина,на пути отраженных лучей собир.линза, кот. собирает их в одной из точек экране, расположенного в фок.плоскости линзы. При ∆=mλ0 получаются максимумы, при ∆=(m+0,5)λ0 - минимумы интенсивности,m-целое число. Условие
максимума для тонкопарал. пластинки:
2b√(
n2-sin2(ϑ1)
) – λ0/2=
mλ0.
Пусть
пластинка освещена рассеянным(лучи
падают под различными углами)
монохроматич. светом. Лучи,параллельные
пл-ти рисунка и падающие на пластинку
под углом ϑ1,соберутся
в т Р’.Лучи, идущие в др плоскостях
и падающие под тем же углом, соберутся
линзой в др точках, отстоящих от экрана
О на такое же расстояние, как и т Р’.
Лучи, падающие под одним и тем же
углом, создадут на экране совокупность
одинаково освещ. точек, расположенных
по окр-ти с центром в т.О.В результате
на экране возникнет система светлых
и темных круговых полос с центром в
т.О.Эти полосы-полосы равного наклона.
|
Временная
когеренстност: ∆˂ lког=
λ2/∆λ
≈ λ02/∆λ0,сл-но
должно соблюдаться усл 2b√(
n2-sin2(i1)
) – λ0/2
˂ λ02
/
∆λ0
или b приходящие в точку P’ лучи 1’ и 2’ отстоят на расстоянии ρ’.Если ρ’˃ρког(hког) падающей волны,то лучи 1’ и 2’ будут когерентными и создадут в точке Р’ освещенность,опредялемую значением ∆, отвечающим углу падения ϑ1’.Др пары лучей,идущие под тем же углом ϑ1’,создадут в остальных точках экрана такую же освещенность. Когда ∆=(m+0.5)λ0 экран темный.При изменении ϑ1’освещенность экрана будет меняться.Из рис. видно,что:ρ=2b tgϑ2 cos ϑ1 = b sin2ϑ2 / √( n2-sin2(ϑ1) ).При угле падения 45º можно положить ρ≈b Просветление оптики. Прохождение света через поверхность линзы сопровождается отражение ≈4% падающего света.В сложных объективах такие отражения многократны,теряется большой световой поток+появляются блики.Чтоб это не происходило на каждую свободную пов-ть линзы наносится тонкая пленка вещ-ва с показ.преломления n≈√(n1n2), n1 и n2 – показ.преломления сред,между которыми нах-ся пленка.При этом интенсивность обеих отраженных от пов-тей пленки волн одинакова.Толщина пленки подбирается такой,чтоб волны,отраженные от обеих пов-тей пленки,оказывались в противофазе,т.е. гасили друг друга.
|
|
|
|
|
|
Эта величина характеризует резкость интерференционной картины. При значениях F много больших единиц, функция пропускания пластинки T(d) имеет вид набора равноотстоящих друг от друга пиков. Фактор резкости тем больше, чем выше коэффициент отражения R на гранях пластинки. При коэффициенте отражения R = 0,99 фактор резкости F = 4´104, а функция пропускания пластинки представляет собой набор дискретных линий (рис. 5.6). Плоскопараллельная пластинка, имеющая пренебрежимо малые потери, связанные с поглощением и рассеянием света, и коэффициентом отражения на гранях, близким к единице, называется эталоном Фабри-Перо.
Из рис. 5.7 видно, что плоскопараллельная пластинка с зеркальными гранями пропускает излучение некоторого дискретного набора частот и совершенно непрозрачна для остального излучения. Таким образом, эталон Фабри-Перо представляет собой высокодобротный частотный фильтр. В этом качестве он используется для управления шириной спектра лазерного излучения. В спектроскопии такие фильтры используют для калибровки длины волны излучения.
|
|
. При
небольшом числе закрытых зон
|
|
|
41. Дифракция Френеля на крае полуплоскости. Поместим
на пути световой волны непрозрачную
полуплоскость с прямолинейным краем.
Расположим её так , чтобы она совпала
с одной из волновых поверхностей. На
расст. b
ща полуплоскостью поставим экран ,
на котором возьмем т. P.
Разобьем на зоны откр. часть волновой
поверхности , имеющие вид очень узких
прямолинейных полосок , параллельных
краю полуплоскости. Ширину зон выберем
так , чтобы отсчитанные в плоскости
рисунка расстояние от т. P
до краев любой зонв отличалась на
Зоны m и m’ имеют одинаковую ширину и расположены относительно т. P симметрично.
|
42. Дифракция Френеля на щели. Спираль Корню. Задача
о дифр. Френеля от щели может быть
решена с помощью спирали Корню. Волнов.
Поверхность падающего света , плоскость
щели и экран , будем считать параллельных
друг другу. Рис.1. Для точки P , лежащей посередине цели , начало и конец результ. Вектора находится в симметр. Относительно начала координат точках спирали.
|
|
43.
Дифракция Фраунгофера на щели.
На бесконечно длинную щель падает
плоская световая волна. Поместим за
щелью собирательную линзу, а в её
фокальной плоскости- экран.Разобьём
открытую часть волновой поверхности
на зоны шириной dx. Волны, посылаемые
зонами под углом φ
к оптической оси линзы, соберутся в
точке экрана P. Каждая зона создаст в
P колебание dξ
=K*(a0dS/r)
cos(ωt-kr+α0),
(множитель 1/r будет отсутствовать,
т.к. в фокальн. пл-сти собираются только
плоские волны, из-за маленьких углов
φ
коэффициент K=const). Площадь зоны
пропорциональна её ширине, значит
амплитуда колебания dξ:
dA=Cdx, C=const. A0= OP
и QP-таутохронны(одинаковая
оптическая длина пути), поэтому
разность фаз между 2мя колебаниями
возникает на пути ∆=xsin φ. Если начальная
фаза колебания в P, возбуждаемого
зоной, находящейся в точке О, будет
равна
|
44.Дифракционная
решётка.
Дифракционной
решёткой называется совокупность
большого числа одинаковых, отстоящих
друг от друга на одно и то же расстояние
щелей. Расстояние d между серединами
соседних щелей называется периодом
решётки. Расположим параллельно
решётке собирающую линзу, в фокальной
плоскости которой поставим экран.
Картины от всех щелей придутся на
одно и то же место(центральный max лежит
против центра линзы). Т.к. колебания,
приходящие в точку P от N
щелей- когерентны, поэтому результирующая
интенсивность будет отличаться от
NIφ
(Iφ-интенсивность,
создаваемая одной щелью). Будем
предполагать, что радиус когерентности
падающей волны намного превышает
длину решётки, поэтому колебания от
всех щелей можно считать когерентными
относительно друг друга. Тогда
результирующее колебание является
суммой N колебаний с одинаковой
амплитудой Aφ,
сдвинутых относительно друг друга
по фазе на одну и ту же величину
Iреш=Iφ
Iреш=Iφ |
|
45. Положение и угловая ширина главных дифракционных максимумов дифракционной решетки. Расположим
параллельно решётке собирающую линзу,
в фокальной плоскости которой поставим
экран. Картины от всех щелей придутся
на одно и то же место(центральный max
лежит против центра линзы). Iреш=Iφ
Iреш=Iφ m≤d/
|
46.Дисперсия
и разрешающая способность дифракционной
решетки.
Положение главных max дифракционной
решётки зависит от длины волны
|
|
48.Дифракция
на моно- и поликристаллах. Лауэграммы
и дебаэграммы (качественно).
Дифракция рентгеновских лучей
применяется для изучения структуры
кристаллов. Определяя направления
максимумов , получающихся при дифракции
исследуемого рентгеновского излучения
от кристаллов с известной структурой,
вычисляется длина волн. Метод
Лауэ:
пучок рентгеновского излучения
направляется на неподвижный
монокристалл. Для каждой системы
слоёв, достаточно густо усеянных
атомами, находится в излучении длина
волны, при которой выполняется: (1)
2dsinϑ=±mλ
(m=1,2,..).
Поэтому на помещённой за кристаллом
фотопластинке получается совокупность
чёрных пятнышек. Взаимное расположение
пятнышек отражает симметрию кристалла.
По расстояниям между пятнышками и по
их интенсивности удаётся найти
размещение атомов в кристалле и
расстояния между ними.
Метод Дебая и Шерера: используется монохроматическое рентгеновское излучение и поликристаллические образцы. Исследуемое вещество измельчается в порошок, из которого прессуется образец в виде проволочки. Образец устанавливается по оси цилиндрической камеры, на боковую поверхность которой укладывается фотоплёнка. |
|
|
Френелевская дифр. картина от щели представляет собой либо светлую , либо темную центральную полосу , но обе стороны которой расположены симметр. Относительно неё чередующегося темную и светлые полосы (рис 4 – темные полосы , рис 3- светлые).
|
|
|
Условие
доп. min:
bsinφ=± Штриховая линия изображает интенсивность от одной щели, умноженную на N^2. Если будет выполняться: m/d=k/b -> m/k=d/b, то m максимум наложится на k минимум. Количество главных max: m≤d/
Угловая
дисперсия:
D= |
Модуль
выражения в квадратных скобках даёт
амплитуду результирующего колебания
в точке P, кот. определяется углом φ:
Aφ=│
|
|
Линейная
дисперсия:
Dлин
= Dлин
=
|
47.Дифракция
рентгеновских лучей. Формула
Брегга-Вульфа.
Если взять прозрачную пластинку с
нанесёнными на неё двумя системами
взаимноперпендикулярных штрихов, то
дифракционная картина будет иметь
вид правильно расположенных пятен,
каждому из которых соответствуют 2
целочисленных индекса- m1
и m2.
d1sinφ1=±m1λ
(m1=0,1,..)-
горизонтальные максимумы, d2sinφ2=±m2λ
(m2=0,1,..)-
вертикальные. Подобная пластинка
представляет собой двумерную
периодическую структуру(d1
и
d2
–
периоды структуры). Если направления,
в которых структура периодична
образуют не прямой угол, до дифракционные
max располагаются в вершинах не
прямоугольников, а параллелограммов.
Для возникновения дифракц.максимумов
необходимо, чтобы d был больше λ или
при m1
и m2
равных 0. Дифракция наблюдается и в
трёхмерных структурах. Таковыми
являются все кристаллические тела,
но условие d>>λ
выполняется только для рентгеновских
лучей. Проведём в направлениях, по
которым свойства структуры обнаруживают
периодичность, оси ox, oy,oz.
|
|
50. Эллиптическая и круговая поляризация света. Расссмотрим два взаимно перпендикулярных электрических колебания, различающихся по фазе на δ
При
разности фаз δ отличной от 0, Если итоговый вектор E вращается по часовой стрелке – правая поляризация, против часовой стрелки – левая поляризация
|
В
огромном количестве беспорядочно
ориентированных кристалликов найдётся
множество таких, для которых окажется
выполненным условие (1), причём
дифрагированный луч будет для разных
кристалликов лежать во всевозможных
плоскостях. В результате для каждой
системы атомных слоёв и каждого m
получится не одно направление
максимума, а конус направлений, ось
которого совпадает с направлением
падающего пучка. Каждая пара симметрично
расположенных линий соответствует
одному из дифракционных максимумов,
удовлетворяющих условию (1) при
некотором значении m. Расшифровка
рентгенограммы позволяет определить
структуру кристалла. |
|
51. Частично поляризованный свет. Степень поляризации. Поляризованным
называется свет, в котором направления
колебаний светового вектора упорядочены
каким-либо образом. Плоскополяризованный
свет можно получить из естественного
света с помощью приборов, называемых
поляризаторами. Эти приборы свободно
пропускают колебания, параллельные
плоскости, которую мы будем называть
плоскостью поляризатора, и полностью
или частично задерживают колебания,
перпендикулярные к его плоскости.
Поляризатор, задерживающий
перпендикулярные к его плоскости
колебания только частично, мы будем
называть несовершенным. На выходе из
несовершенного поляризатора получается
свет, в котором колебания одного
направления преобладают над колебаниями
других направлений. Такой свет
называется частично поляризованным.
Степень поляризации:
|
53.Поляризация при отражении и преломлении. Угол Брюстера. Если
угол падения света на границу раздела
двух диэлектриков отличен от нуля,
отраженный и преломленный лучи
оказываются частично поляризованными.
В отраженном луче преобладают
колебания, перпендикулярные к
плоскости падения (на рис. эти колебания
обозначены точками), в преломленном
луче — колебания, параллельные
плоскости падения (на рисунке они
изображены двусторонними стрелками).
При некотором значении угла падения
|
|
54. Ход светового луча в одноосном кристалле. При
прохождении света через все прозрачные
кристаллы, за исключением кубической
системы, наблюдается явление,
заключающееся в том, что упавший на
кристалл луч разделяется внутри
кристалла на два луча, распространяющихся,
вообще говоря, с разными скоростями
и в различных направлениях. Это явление
носит название двойное
лучепреломление. Кристаллы,
обладающие двойным лучепреломлением,
подразделяются на одноосные и двуосные.
У одноосных кристаллов один из
преломленных лучей подчиняется
обычному закону преломления: он лежит
водной плоскости с падающим лучом и
нормалью к преломляющей поверхности.
Этот луч называется
обыкновенным лучом и
обозначается о.
Для другого
луча, называемого необыкновенным
(обозначатся
е),
отношение синусов угла падения и угла
преломления остается постоянным при
изменении угла падения. У одноосных кристаллов имеется направление, вдоль которого обыкновенный и необыкновенный лучи распространяются не разделяясь и с одинаковой скоростью. Это направление называется оптической осью кристалла. Двойное
лучепреломление объясняется
анизотропией кристаллов: в некубических
системах диэлектрическая проницаемость
оказывается зависящей от направления.
В одноосных кристаллах
|
55. Кристаллическая пластинка между двумя поляризаторами.
Поместим
между 2 поляр-ми P
и P’
пластинку из одноосного кристалла,
вырезанную параллельно оптической
оси О. из P выйдет плоскополяризованный
свет интенсивности I. Пройдя через
пластинку, свет станет поляризованным
по эллипсу. При выходе из p' станет
снова плоскополяризованным. I' зависит
от взаимн. ориентации плоскостей P
и P’
и разности фаз δ, возникающей при
прохождении через пластинку. Рассм.2
случая: 1)P||P’(а),
2)P
и P’-
скрещены(б). Световое колебание,
вышедшее из P, изобразится век-ром E,
леж. в плоскости P. При входе в пластинку
E
возбудит 2 колебания- E0(обыкновенн.
луч), Ee(необыкнов.луч).
Колебания будут когерентны и приобретут
разность фаз δ, которая определяется:
δ=2π(Δ/λ0)=2π[(no-ne)
/λ0]
Амплитуды колебаний: E0=Esinφ,
Ee=Ecosφ.
Если φ=45, то амплитуды одинаковы и
равны E/
(случай
а)
Через P’пройдут
составляющие колебаний с амплитудами:
E'0||=E0sinφ=E (E’||)^2= (E’0||)^2 +(E’e||)^2 + 2 E’e|| E’0||cosδ. Подставим значение (1)=> (E’||)^2=(E^2)cos^2(δ/2).-> I||’= Icos^2(δ/2) (2). I-интенс.света, прошедш.через поляриз. P, I’||- интенсивн. по выходе из поляриз.P'. (Случай б) амплитуды E'0﬩ и E'e﬩, получающиеся при выходе из P' по значениям будут равны (1). Но в дополнение к разности фаз возникает дополнительн.разность фаз π. Тогда: I'﬩= Icos^2[(π+δ)/2]=Isin^2(δ/2) (3). Из (2) и (3) => при δ=2κπ (κ=0.1,..) интенс. I||’=0, а I'﬩=I.
|
|
56.
Прохождение плоскополяризованного
света через кристаллическую пластинку.
Пластинка в четверть и половину длины
волны. Рассмотрим кристаллическую пластинку, вырезанную параллельно оптической оси. При падении на такую пластинку плоскополяризованного света обыкнов. и необыкнов. Лучи оказываются когерентными. За время прохожд. через пластину между лучами возникн.разность хода ∆=(n0-ne)d и разность фаз δ=2π( n0-ne)d /λ0 (1), где d-толщина пластинки, λ0-длина волны в вакууме.
|
57. Элементарная теория дисперсии. Дисперсия света – явление, обусловленное зависимостью показателя преломления вещества от частоты. Она может быть объяснена на основе электромагнитной теории и электронной теории вещества. Для этого необходимо рассмотреть процесс взаимодействия света с веществом. Рассмотрим квазиупруго связанные внутри атома электроны, которые при прохождении через вещество электромагнитной волны начинают колебаться по закону
Где правая часть – выражения для силы, действующей на электрон. Пусть молекулы вещества неполярны, дипольный электрический момент вещества
Где
N
– число
молекул в единице вещества (суммирование
производится по всем электронам,
входящим в состав молекулы; направления
смещений
Диэлетрическая проницаемость вещества равна
Заменяя
|
|
58. Групповая и фазовая скорости. Строго монохроматическая волна вида
представляет собой последовательность «горбов» и «впадин» перемещающихся вдоль оси х с фазовой скоростью:
Свет,
даже монохроматический, представляет
собой наложение волн с частотами в
интервале ∆
В том
месте, где суммарная волна будет иметь
максимум амплитуды, располагается
центр группы волн. Если
все составляющие перемещаются с
одинаковой скоростью
|
59. Групповая и фазовая скорости. Строго монохроматическая волна вида
представляет собой последовательность «горбов» и «впадин» перемещающихся вдоль оси х с фазовой скоростью:
Свет,
даже монохроматический, представляет
собой наложение волн с частотами в
интервале ∆
В том
месте, где суммарная волна будет иметь
максимум амплитуды, располагается
центр группы волн. Если
все составляющие перемещаются с
одинаковой скоростью
|
|
Эти формулы вытекают из условий, налагаемых на электромагнитное поле на границе двух диэлектриков. Обозначим: Â11 и Â1 – амплитуды падающих волн; Â’11 и Â’1 – амплитуды отраженных волн; ”11 и ”1 – амплитуды преломленных волн, то формулы Френеля имеют следующий вид(11 – знак параллели и 1 – знак перпендикуляра):
Возведя уравнения в квадрат и умножив получившиеся выражения на показатель преломления среды, получим
|
52. Двойное лучепреломление в одноосных кристаллах. При прохождении света через почти все прозрачные кристаллы, наблюдается явление, получившее название двойного лучепреломления. Упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющиеся с разными скоростями и в различных направлениях. Кристаллы, обладающие двойным лучепреломлением, подразделяются на одноосные и двуосные. У одноосных кристаллов один из преломленных лучей подчиняется обычному закону преломления. Этот луч называется обыкновенным и обозначается буквой о. Для другого луча, называемого необыкновенным , отношение синусов угла падения и угла преломления не остается постоянным при изменении угла падения. Примерами одноосных кристаллов могут служить исландский шпат, кварц и турмалин. У одноосных кристаллов имеется направление (оптическая ось кристалла), вдоль которого обыкновенный и необыкновенный лучи распространяются не разделяясь и с одинаковой скоростью. Любая плоскость, проходящая через оптическую ось, называется главным сечением или главной плоскостью кристалла. Исследование обыкновенного и необыкновенного лучей показывает, что оба луча полностью поляризованы во взаимно перпендикулярных направлениях.
|
|
Наверно не нужно: Разность показателей преломл. n0-ne завис. от длины волны света λ0. Пусть свет, падающ. на поляриз. P, состоит из излучения 2х длин волн- λ1, λ2(δ.для λ1 удовл.(2), а для λ2 удовл.(3)). Тогда при // поляриз-ах через пластинку и поляриз.P' пройдёт свет с λ1, а свет с λ2- полностью задержится). В случае б будет наоборот. Значит при различ. располож. поляриз-ов окраска прошедшего света будет соотв либо длине волны λ1, либо λ2. Такие 2 окраски назыв. дополнительными. При вращении одного из поляриз-ов окраска непрерывно меняется, переходя за каждые четверть оборота от одного дополн.цвета к другому. То же самое наблюд. при φ≠π/4(но не равн. 0 или π/2). Разность фаз δ завис. от толщины пластинки. Поэтому, если двоякопреломляющая прозрачн.пластинка, перемещённая между поляр-ми, имеет в разн. местах разную толщину, эти места при наблюдении со стороны P' будут представляться окраш.в разные цвета. При вращении P' эти цвета изменяются, причём каждый из цветов переходит в дополнительн. к нему цвет.
|
В
других направлениях
В обыкновенном луче колебания светового вектора происходят в направлении, перпендикулярном к главному сечению кристалла (рис.1, направление 1). Поэтому при любом направлении обыкновенного луча вектор Е образует с осью кристалла прямой угол и скорость волны будет равна
Волновая поверхность обыкновенных лучей – сфера. Колебания
в необыкновенном луче совершаются в
главном сечении, поэтому для луча 2
скорость имеет значение
Для луча 3 скорость имеет промежуточное значение. Волновой пов-ю необыкновенных лучей является эллипсоид вращения. Показатели преломления обыкновенного и необыкновенного луча соответственно
В
зависимости от того, какая из скоростей
больше
|
|
График
зависимости квадрата показателя
преломления от частоты, где
|
Вырезанная параллельно оптической оси пластинка, для кот. ( n0-ne)d=m λ0+ λ0/4 называется пластинкой в четверть длины волны. При прохождении через неё обыкнов. и необыкн. свет приобретает разность фаз =π/2. Пластинка, для кот. ( n0-ne)d=m λ0+ λ0/2- пластинка в полволны. . На выходе из неё между обыкнов. и необыкн. волнами возникает разность фаз =π. Рассмотрим прохождение плоскополяризованного света через пластинку в полволны. Пусть колебание в падающем луче Е, совершающееся в плоскости Р, возбудит при входе в кристалл Ео и Ее. После прохождения пластинки разность фаз между Ео и Ее изменится на π и станет соответствовать Е’о и Ее. Следовательно свет на выходе будет поляризован в плоскости Р’, причем он будет повёрнут относительно Р на 2φ. Аналогичными
рассуждениями можно получить для
четвертьволновой пластинки , что если
угол между плоскостью колебаний Р в
падающем луче и осью пластинки О
φ=π/4, то свет вышедший из пластинки
будет поляризован по кругу, в остальных
случаях, свет будет поляризован по
эллипсу.
|
|
Если же наблюдается дисперсия, то центр группы волн будет перемещаться с групповой скоростью
если
Далее соотношение
из
|
Если же наблюдается дисперсия, то центр группы волн будет перемещаться с групповой скоростью
если
Далее соотношение
из
|
|
60. Комплексный показатель преломления вещества. Пусть электромагнитая волна, описываемая уравнением
Или в экспоненциальной записи
Проходит
сквозь пластинку с показателем
преломления n.
Учитывая время на прохождение волной
пластинки, равное
|
62. Закон Релея и объяснение голубого цвета. Молекулярное рассеяние света. Поглощение света и закон Бугера. Свет, проходящий через вещество, вызывает колебания электронов в атомах. Колеблющиеся электроны, в свою очередь, возбуждают вторичные волны, распространяющиеся по всем направлениям. Если учитывать интерференцию этих волн, то рассеяние происходит не по всем направлениям. В случае однородной среды вторичные волны гасят друг друга во всех направлениях, кроме направления распространения направления первичной волны. Поэтому перераспределения света по направлениям, т.е. рассеяния, не происходит. В случае неоднородной среды вторичные волны не погашают друг друга в боковых направлениях. Световые волны, дифрагируя на неоднородностях среды, дают дифракционную картину, характеризующуюся довольно равномерным распределением интенсивности по всем направлениям. Такую дифракцию на мелких неоднородностях называют рассеянием света. Среды с явно выраженной оптической неоднородностью носят название мутных сред( дымы, туманы, взвеси и суспензии, эмульсии, твердые тела вроде перламутра, опалов, молочных стекол и т.п.).
|
|
63. Поглощение света и закон Бугера. При прохождении световой волны через вещество часть энергии волны затрачивается на возбуждение колебаний электронов. Частично эта энергия вновь возвращается в излучение в виде вторичных волн, частично она переходит во внутреннюю энергию вещества – энергию движения атомов, поэтому интенсивность света при прохождении через вещество уменьшается – свет поглощается в веществе. Вынужденные колебания электронов становятся особенно интенсивными при резонансной частоте. Опыт показывает, что при прохождении через вещество интенсивность убывает по закону Бугера:
Где
Коэффициент поглощения зависит от частоты волны. У веществ с низким взаимодействием атомов или молекул(газы) коэффициент поглощения практически равен нулю и лишь для узких спектральных областей, соответствующих резонансным частотам колебаний частиц вещества, наблюдаются резкие максимумы (рис.1). Металлы для света также практически непрозрачны из-за наличия свободных электронов, (световая энергия быстро убывает, превращаясь в кинетическую энергию электронов) У твердых и жидких тел, а также газов под высоким давлением полосы поглощения гораздо шире (рис.2). |
|
|
|
|
|
|
|
|
Свет, рассеянный на частицах, размеры которых много меньше длины световой волны, оказывается частично поляризованным. В случае, когда колебания вектора Е вторичной волны происходит в плоскости, проходящей через направление колебаний зарядов, свет, рассеиваемый частицами в направлениях перпендикулярных пучку, , будет полностью поляризован. В результате в случае мутных веществ закон Бугера выглядит следующим образом:
Где
Если размеры неоднородностей малы по сравнению с длиной волны (не более 0,1λ), то выполняется закон Релея интенсивность света пропорциональна четвертной степени частоты (обратно пропорциональна четвертной степени длины волны)
Даже очищенные от посторонних примесей жидкости и газы рассеивают свет, что вызвано флуктуациями плотности вследствие беспорядочного движения молекул вещества. Данный вид рассеяния называется молекулярным. Именно этим видом рассеяния объясняется голубой цвет неба: согласно закону Релея, синие и голубые лучи рассеиваются сильнее, чем желтые и красные. Когда же Солнце находится низко над горизонтом, его лучи проходят большую толщу рассеивающей среды и они оказываются обогащенными большими длинами волн, в результате чего небо окрашивается в красные тона
|
Теперь пусть показатель преломления – комплексная величина
Подставляя в уравнение волны и перегруппировывая члены, получаем
Таким образом, вещественная часть показателя преломления n’ показывает запаздывание волны по фазе при прохождении пластинки, а мнимая часть n’’ – затухание волны по амплитуде. Поэтому n’’ иногда еще называю коэффициентом затухания.
|
|
|
Рис 1. Рис 2. |

 Для
произвольного x:
Для
произвольного x: .
.
 -начальная
фаза волны, a-
амплитуда волны,
-начальная
фаза волны, a-
амплитуда волны, -
скорость распространения.
-
скорость распространения.
 cos(
cos(
 cos(
cos(
 -
амплитуда в т. плоскости x=0.
-
амплитуда в т. плоскости x=0.
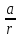 cos(
cos(
 exp(
exp( r)cos(
r)cos(

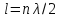 данным
длинам волн соответствуют частоты:
данным
длинам волн соответствуют частоты:

 ,
где
,
где
 -
напряжение (Н/
-
напряжение (Н/ ),
E-
модуль Юнга,
),
E-
модуль Юнга,
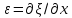 .
.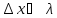 в момент, когда при расхождении волны
он оказался, например, в растянутом
состоянии (рис.). Тонкий
стержень-величина
которого мала по сравнению с длиной
в момент, когда при расхождении волны
он оказался, например, в растянутом
состоянии (рис.). Тонкий
стержень-величина
которого мала по сравнению с длиной
 .
.

 =
= (
(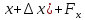 (
(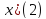 ,
где
,
где
 - плотность материала стержня, S
– площадь поперечного сечения. Правую
часть уравнения можно переписать в
виде:
- плотность материала стержня, S
– площадь поперечного сечения. Правую
часть уравнения можно переписать в
виде:
 (
( (
( =
= )-
)- )=S
)=S ,
(
,
( (
( (
(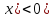 .
Сокращая
(2) на
.
Сокращая
(2) на
 ,
получим
,
получим
 =
= .
Учитывай (1), имеем:
.
Учитывай (1), имеем: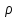
 =
=
 - это
волновое уравнение для тонкого
стержня.
- это
волновое уравнение для тонкого
стержня.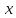 :
:
 =
= (1)
(1)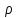
 =
=
 (2)
(2) ,
, - плотность материала стержня.
- плотность материала стержня. ,
, -
модуль сдвига.
-
модуль сдвига.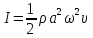 (1)
(1)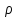 -
плотность невозмущенного газа,
-
плотность невозмущенного газа,
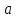 -
амплитуда колебаний частиц среды,
-
амплитуда колебаний частиц среды,
 -
частота,
-
частота,
 -
фазовая скорость.
-
фазовая скорость.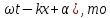
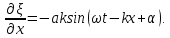
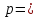 -
-
 .
Отсюда
.
Отсюда ,
подставим
в (1)
,
подставим
в (1)
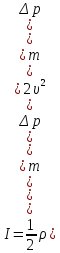
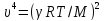 ,
а
,
а

 :
:


 =
=
 x
; x∆m=ρ∆xS
; Fx=SPx-∆x=S(Px+ξ
-Px+∆x+ξ+∆ξ)=S(Px+(
x
; x∆m=ρ∆xS
; Fx=SPx-∆x=S(Px+ξ
-Px+∆x+ξ+∆ξ)=S(Px+( -Px-(
-Px-( |x(x+∆x+ξ+∆ξ))=S(
|x(x+∆x+ξ+∆ξ))=S( ∆x;
∆x;
 =const;
∆V=S∆x;
=const;
∆V=S∆x; =P’∆
=P’∆ =
=



 ∆P/P =γ(
∆P/P =γ(
 );
ρ
);
ρ =-(
=-( ;
; =-γ
=-γ ;
P’=P+∆P ;
;
P’=P+∆P ; ∆ξ=(
∆ξ=(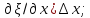


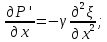 ρ
ρ =γP
=γP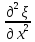 ; P=(ρ/μ)RT ;
; P=(ρ/μ)RT ;

 =(γRT/μ)
=(γRT/μ) ;
;

 =
= - классическое уравнение звуковой
волны.
- классическое уравнение звуковой
волны. ; T≈290K;
V=340
м/с – в воздухе.
; T≈290K;
V=340
м/с – в воздухе.
 данным
длинам волн соответствуют частоты:
данным
длинам волн соответствуют частоты:

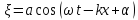


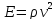
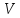
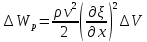
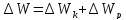
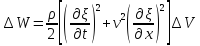

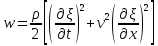



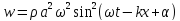 т.к. среднее
значение квадрата синуса равно 1/2, то
т.к. среднее
значение квадрата синуса равно 1/2, то


 . направление вектора плотности потока
энергии совпадает с направлением
переноса энергии.
. направление вектора плотности потока
энергии совпадает с направлением
переноса энергии.


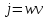

 - вектор Умова
- вектор Умова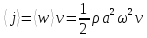
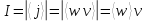




 – частота, воспринимаемая
приемником,
– частота, воспринимаемая
приемником, частота
колебаний источника
частота
колебаний источника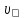 – скорость распространения волны
относительно среды
– скорость распространения волны
относительно среды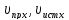 - проекции скоростей приемника и
источника на ось х
- проекции скоростей приемника и
источника на ось х

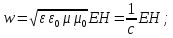


 .
Плотность потока энергии равна:
S=ωc=
.
Плотность потока энергии равна:
S=ωc= .
.


 и
и
 (их проекции на Ох и Оz)
не будут зависеть от координат у и z,
производные по у и z
равны нулю. ур-я максвелла примут вид:
(их проекции на Ох и Оz)
не будут зависеть от координат у и z,
производные по у и z
равны нулю. ур-я максвелла примут вид:
 ,
,
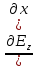 =
=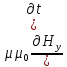 ;
;
 =
=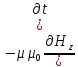 (1)
(1)
 =
= =0
(2)
=0
(2) ,
, ;
;
 (3)
(3)
 =0
(4)
=0
(4)
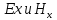 не зависят ни от x,
ни от t.
Сл-но отличные от нуля
не зависят ни от x,
ни от t.
Сл-но отличные от нуля
 могут быть обусловлены лишь постоянными
однородными полями, накладывающимися
на электромаг. Поле волны. Само поле
не имеет составляющих вдоль Ох. Отсюда
вытекает, что
могут быть обусловлены лишь постоянными
однородными полями, накладывающимися
на электромаг. Поле волны. Само поле
не имеет составляющих вдоль Ох. Отсюда
вытекает, что
 и
и
 ⊥
к направлению распределения волны,
т е электромаг. волны поперечны.
⊥
к направлению распределения волны,
т е электромаг. волны поперечны. =
= ,
,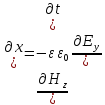 (5)
(5)
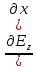 =
= ,
, (6)
(6)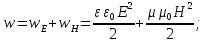
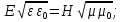




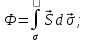


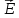 и
и
 связаны соотношением:
связаны соотношением:
 ;
;
 :
:
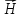 на
на
 :
:
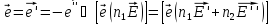

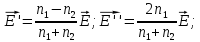
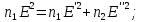




 E
(
E
( -удельная
проводимость), а магнитное поле волны
будет действовать на j
в соответствии
с законом
Ампера –
с силой, объёмная плотность которой
равна:
-удельная
проводимость), а магнитное поле волны
будет действовать на j
в соответствии
с законом
Ампера –
с силой, объёмная плотность которой
равна: [EB]
, откуда
следует, что сила направлена в сторону
распространения волны.
[EB]
, откуда
следует, что сила направлена в сторону
распространения волны. ,
то согласно (6) появится поле
,
то согласно (6) появится поле
 ,
которое возбудит
,
которое возбудит
 и
тд. ТО для описания электром. волны
достаточно взять одну из систем (5)
или (6) положив компоненты другой
системы равными нулю. пусть
и
тд. ТО для описания электром. волны
достаточно взять одну из систем (5)
или (6) положив компоненты другой
системы равными нулю. пусть =
= =0.
=0. )=
)=
 )
подставив из (5)
)
подставив из (5)
 получим
получим
 (7)аналогично
(7)аналогично (8).
(7) имеет решение
(8).
(7) имеет решение
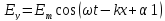 ;
(8):
;
(8):
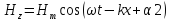 ;
подставив в (5) получим:
;
подставив в (5) получим:
 =
=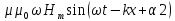 ;
; =
=
 ,
,

 =>
=> =
=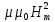 ,
то
,
то
 =
=


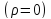 непроводящей
непроводящей
 среды с постоянными проницаемостями
среды с постоянными проницаемостями
 :
: ,
,
 ,
,
 ,
,
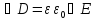
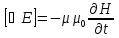 ,
,
 ,
,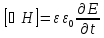 ,
,
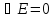
 ,
,




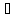
 ,
,

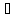


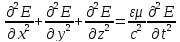

 - фазовая скорость этой волны
- фазовая скорость этой волны
 ν/ν=Vx/c.
Эффект Доплера нашел многочисленные
практические применения. С его помощью
определяют скорость излучающих атомов
в пучке, угловую скорость вращения
Солнца и т.д.
ν/ν=Vx/c.
Эффект Доплера нашел многочисленные
практические применения. С его помощью
определяют скорость излучающих атомов
в пучке, угловую скорость вращения
Солнца и т.д.










 λ
область перекрытия волн PQ
имеет протяженность 2b
tgα
≈ 2bα
N-макс
число полос, N=PQ/∆x=2brα2
/
λ(r+b)
Чтоб эти полосы были действ видны,
необ чтоб N/2
не превышало mпределный,
mпределный
≈
λ/∆λ
λ
область перекрытия волн PQ
имеет протяженность 2b
tgα
≈ 2bα
N-макс
число полос, N=PQ/∆x=2brα2
/
λ(r+b)
Чтоб эти полосы были действ видны,
необ чтоб N/2
не превышало mпределный,
mпределный
≈
λ/∆λ









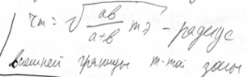 .
. .
+ соответствует нечетным m
и минус-четным.
.
+ соответствует нечетным m
и минус-четным.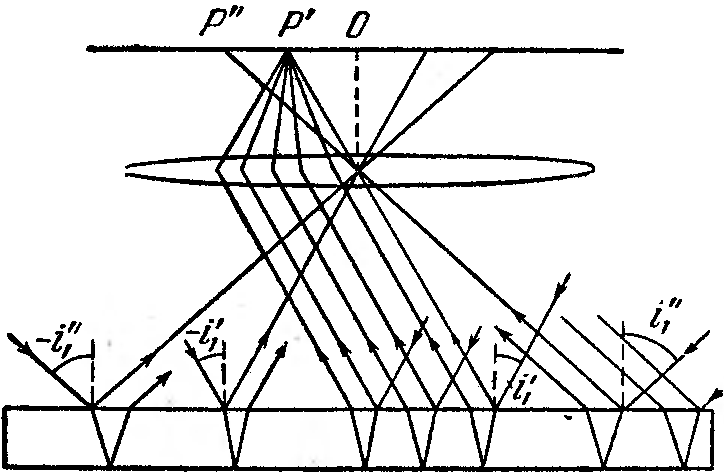
 0,5многоменьше λ0/∆λ0
и √( n2-sin2(i1)
) порядка 1,получаем b
0,5многоменьше λ0/∆λ0
и √( n2-sin2(i1)
) порядка 1,получаем b Простран. когерентность:
Простран. когерентность:



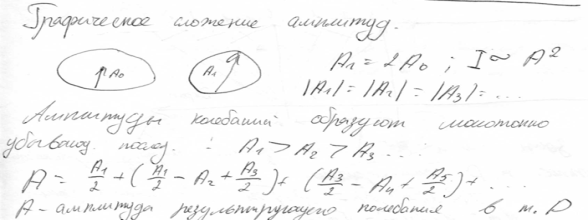

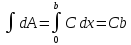 ->
C=A0/b
(b-ширина щели). Значит
dA=(A0/b)dx.
->
C=A0/b
(b-ширина щели). Значит
dA=(A0/b)dx.

 ,
то фаза колебания от зоны, находящ. в
точке x:
,
то фаза колебания от зоны, находящ. в
точке x:
 (
( -длина
волны в среде). Колебание, возбуждаемое
зоной с координатой x:
-длина
волны в среде). Колебание, возбуждаемое
зоной с координатой x:
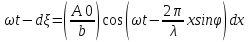 .
Найдём результирующее колебание,
возникающее в P:
.
Найдём результирующее колебание,
возникающее в P:
 .
.

 .
Разность хода от соседних щелей равна
∆=dsinφ
-> разность фаз
.
Разность хода от соседних щелей равна
∆=dsinφ
-> разность фаз
 , где
, где
 -
длина волны в данной среде. Получим:
-
длина волны в данной среде. Получим: (I0-
интенсивность, создаваемая одной
щелью против центра линзы). Первый
множитель обращается в 0, если: bsinφ=±k
(I0-
интенсивность, создаваемая одной
щелью против центра линзы). Первый
множитель обращается в 0, если: bsinφ=±k (k=1,2,..)
В этих точках интенсивность, создаваемая
от каждой щели в отдельности, равна
0. Для направлений, для которых
(k=1,2,..)
В этих точках интенсивность, создаваемая
от каждой щели в отдельности, равна
0. Для направлений, для которых
 ,
т.е. dsinφ=
,
т.е. dsinφ= (m=1,2,..)
(условие, определяющее положение
главных max, где m-
даёт порядок главного max)
колебания отдельных щелей взаимно
усиливают друг друга, поэтому амплитуда
в соответствующей точке экрана:
Amax=NAφ
(Aφ-амплитуда
колебания, посылаемого одной щелью
под углом φ). Imax=Iφ
(m=1,2,..)
(условие, определяющее положение
главных max, где m-
даёт порядок главного max)
колебания отдельных щелей взаимно
усиливают друг друга, поэтому амплитуда
в соответствующей точке экрана:
Amax=NAφ
(Aφ-амплитуда
колебания, посылаемого одной щелью
под углом φ). Imax=Iφ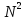 . В промежутках между главными
максимумами имеется N-1 добавочных
минимумов(возникают в направлениях,
в кот. колебания от отдельн. щелей
погашают друг друга.
. В промежутках между главными
максимумами имеется N-1 добавочных
минимумов(возникают в направлениях,
в кот. колебания от отдельн. щелей
погашают друг друга. .
Разность хода от соседних щелей равна
∆=dsinφ
-> разность фаз
.
Разность хода от соседних щелей равна
∆=dsinφ
-> разность фаз
 , где
, где
 -
длина волны в данной среде. Получим:
-
длина волны в данной среде. Получим: (I0-
интенсивность, создаваемая одной
щелью против центра линзы). Для
направлений, для которых
(I0-
интенсивность, создаваемая одной
щелью против центра линзы). Для
направлений, для которых
 ,
т.е. dsinφ=
,
т.е. dsinφ= (m=1,2,..)
(условие, определяющее положение
главных max, где m-
даёт порядок главного max)
колебания отдельных щелей взаимно
усиливают друг друга, поэтому амплитуда
в соответствующей точке экрана:
Amax=NAφ
(Aφ-амплитуда
колебания, посылаемого одной щелью
под углом φ). Imax=Iφ
(m=1,2,..)
(условие, определяющее положение
главных max, где m-
даёт порядок главного max)
колебания отдельных щелей взаимно
усиливают друг друга, поэтому амплитуда
в соответствующей точке экрана:
Amax=NAφ
(Aφ-амплитуда
колебания, посылаемого одной щелью
под углом φ). Imax=Iφ . Количество главных max:
. Количество главных max:
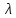 (т.к.
sinφ≤1). Для дополнительных min, ближайших
к главн. максимуму m-го продка: dsinφ=
(т.к.
sinφ≤1). Для дополнительных min, ближайших
к главн. максимуму m-го продка: dsinφ= ->
->
 φm=
φm= -угловая ширина m-го
максимума. Введём: m
-угловая ширина m-го
максимума. Введём: m φm=arcsin(x+∆x)
– arcsin(x-∆x).
Если щелей много, то ∆x- очень мало->
arcsin(x±∆x)≈
arcsinx±(arcsinx)’∆x.
Подставим эти значения:
φm=arcsin(x+∆x)
– arcsin(x-∆x).
Если щелей много, то ∆x- очень мало->
arcsin(x±∆x)≈
arcsinx±(arcsinx)’∆x.
Подставим эти значения:
 φm≈2(arcsinx)’∆x=
φm≈2(arcsinx)’∆x=
 =
= )
(
)
(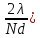 .
Nd-длина
дифракц.решётки.-> угловая ширина
главн.максимумов обратно пропорциональна
длине решётки.
.
Nd-длина
дифракц.решётки.-> угловая ширина
главн.максимумов обратно пропорциональна
длине решётки. .
Поэтому при пропускании через решётку
белого света все максимумы, кроме
центрального, разложатся в
спектр(фиолетовый конец- в центре
дифр.картины, красный- снаружи). Значит
дифр.решётка- спектральный
прибор.Дифракционная решётка сильнее
отклоняет красные лучи. Положения
красного конца спектра m-го порядка
и фиолетого конца спектра (m+1)-го
порядка: sinφкр=0.76m/d
, sinφфиол=0.40(m+1)/d
, d-
в микрометрах. Если 0.76m>0.40(m+1),
то спектры m
и (m+1)
порядков частично перекрываются.
Дисперсия и разрешающая сила- основные
характеристики спектрального прибора.
Дисперсия
определяет
угловое или линейное расстояние между
двумя спектральными линиями,
различающимся по длине волны на
единицу. Разрешающая
сила
определяет минимальную разность длин
волн
.
Поэтому при пропускании через решётку
белого света все максимумы, кроме
центрального, разложатся в
спектр(фиолетовый конец- в центре
дифр.картины, красный- снаружи). Значит
дифр.решётка- спектральный
прибор.Дифракционная решётка сильнее
отклоняет красные лучи. Положения
красного конца спектра m-го порядка
и фиолетого конца спектра (m+1)-го
порядка: sinφкр=0.76m/d
, sinφфиол=0.40(m+1)/d
, d-
в микрометрах. Если 0.76m>0.40(m+1),
то спектры m
и (m+1)
порядков частично перекрываются.
Дисперсия и разрешающая сила- основные
характеристики спектрального прибора.
Дисперсия
определяет
угловое или линейное расстояние между
двумя спектральными линиями,
различающимся по длине волны на
единицу. Разрешающая
сила
определяет минимальную разность длин
волн
 ,
при которой 2 линии воспринимаются в
спектре раздельно. Угловая
дисперсия:
D=
,
при которой 2 линии воспринимаются в
спектре раздельно. Угловая
дисперсия:
D=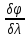 , где
, где
 угловое расстояние между спектральными
линиями, различающимися по длине
волны на
угловое расстояние между спектральными
линиями, различающимися по длине
волны на
 dsinφ=
dsinφ=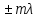 (m=1,2,..)
дифференцируем(справа по
(m=1,2,..)
дифференцируем(справа по
 )->
dcosφ
)->
dcosφ =m
=m D=
D=
 , при небольших углах: D≈
, при небольших углах: D≈
 , значит угловая дисперсия обратно
пропорциональна периоду решётки d.
, значит угловая дисперсия обратно
пропорциональна периоду решётки d.
 49.Свойства
плоской монохроматической
электромагнитной волны. Виды
поляризации. Свет,
в котором направления колебаний
упорядочены каким-либо образом,
называется поляризованным.
Если колебания светового вектора
происходят только в одной проходящей
через луч плоскости, свет назыв.
плоскополяризованным.
Если вектор E
поворачивается
вокруг луча, одновременно пульсируя
по модулю, то конец вектора описывает
эллипс и свет назыв. эллиптически-поляризованным.
Если конец E
описывает окружность, то свет назыв.
поляризованным
по кругу.
В естественном свете колебания
различных направлений быстро и
беспорядочно сменяют друг друга.
Рассмотрим два взаимно перпендикулярных
электрич.колебания, совершающихся
вдоль ox и oy и различающихся по фазе
на
49.Свойства
плоской монохроматической
электромагнитной волны. Виды
поляризации. Свет,
в котором направления колебаний
упорядочены каким-либо образом,
называется поляризованным.
Если колебания светового вектора
происходят только в одной проходящей
через луч плоскости, свет назыв.
плоскополяризованным.
Если вектор E
поворачивается
вокруг луча, одновременно пульсируя
по модулю, то конец вектора описывает
эллипс и свет назыв. эллиптически-поляризованным.
Если конец E
описывает окружность, то свет назыв.
поляризованным
по кругу.
В естественном свете колебания
различных направлений быстро и
беспорядочно сменяют друг друга.
Рассмотрим два взаимно перпендикулярных
электрич.колебания, совершающихся
вдоль ox и oy и различающихся по фазе
на
 :
Ex=A1cos
:
Ex=A1cos ,
Ey=A2
cos
,
Ey=A2
cos .
tg
.
tg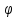 =Ey/Ex=
=Ey/Ex= ,
,
 -угол
между E
и
Ex.
Естественный
свет можно представить, как наложение
двух некогерентных электромагнитных
волн, поляризованных во взаимно
перпендикулярных плоскостях и имеющих
одинаковую интенсивность. Допустим,
что Ex
и
Ey
когерентны,
причём δ=0 или δ=π : tgφ=±A2/A1=const
-> волна плоскополяризованная. Если
A1=A2
и δ=±π/2:
tgφ=
-угол
между E
и
Ex.
Естественный
свет можно представить, как наложение
двух некогерентных электромагнитных
волн, поляризованных во взаимно
перпендикулярных плоскостях и имеющих
одинаковую интенсивность. Допустим,
что Ex
и
Ey
когерентны,
причём δ=0 или δ=π : tgφ=±A2/A1=const
-> волна плоскополяризованная. Если
A1=A2
и δ=±π/2:
tgφ=


 (k
(k =1,2,…,N-1,N+1,..,
2N-1,
2N+1,..).
Между доп. min располагаются слабые
вторичные max. Их число= N-2.
=1,2,…,N-1,N+1,..,
2N-1,
2N+1,..).
Между доп. min располагаются слабые
вторичные max. Их число= N-2.
 (т.к.
sinφ≤1). Для дополнительных min, ближайших
к главн. максимуму m-го продка: dsinφ=
(т.к.
sinφ≤1). Для дополнительных min, ближайших
к главн. максимуму m-го продка: dsinφ= ->
->
 φm=
φm=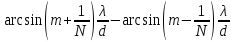 -угловая ширина m-го
максимума. Введём: m
-угловая ширина m-го
максимума. Введём: m φm=arcsin(x+∆x)
– arcsin(x-∆x).
Если щелей много, то ∆x- очень мало->
arcsin(x±∆x)≈
arcsinx±(arcsinx)’∆x.
Подставим эти значения:
φm=arcsin(x+∆x)
– arcsin(x-∆x).
Если щелей много, то ∆x- очень мало->
arcsin(x±∆x)≈
arcsinx±(arcsinx)’∆x.
Подставим эти значения:
 φm≈2(arcsinx)’∆x=
φm≈2(arcsinx)’∆x=
 =
= )
(
)
( .
Nd-длина
дифракц.решётки.-> угловая ширина
главн.максимумов обратно пропорциональна
длине решётки. Положение главных max
зависит от
.
Nd-длина
дифракц.решётки.-> угловая ширина
главн.максимумов обратно пропорциональна
длине решётки. Положение главных max
зависит от
 ,
поэтому при пропускании белого света
через решётку- все максимумы, кроме
центрального, разложатся на спектр.->
дифракционная решётка- спектральный
прибор. Дисперсия определяет угловое
или линейное расстояние между двумя
спектральными линиями, различающимся
по длине волны на единицу. Разрешающая
сила определяет минимальную разность
длин волн
,
поэтому при пропускании белого света
через решётку- все максимумы, кроме
центрального, разложатся на спектр.->
дифракционная решётка- спектральный
прибор. Дисперсия определяет угловое
или линейное расстояние между двумя
спектральными линиями, различающимся
по длине волны на единицу. Разрешающая
сила определяет минимальную разность
длин волн
 ,
при которой 2 линии воспринимаются в
спектре раздельно.
,
при которой 2 линии воспринимаются в
спектре раздельно.
 , где
, где
 угловое расстояние между спектральными
линиями, различающимися по длине
волны на
угловое расстояние между спектральными
линиями, различающимися по длине
волны на
 Линейная
дисперсия:
Dлин
=
Линейная
дисперсия:
Dлин
= , где
, где
 линейное расстояние на экране между
спектральн.линиями, различающимися
на
линейное расстояние на экране между
спектральн.линиями, различающимися
на
 Разрешающая
сила: R=
Разрешающая
сила: R=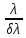 ,
где
,
где
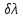 -
минимальная разность длин волн двух
спектральных линий, при которой они
воспринимаются раздельно.
-
минимальная разность длин волн двух
спектральных линий, при которой они
воспринимаются раздельно.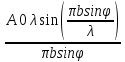 │.
Для точки против линзы φ=0 -> Aφ=A0.
Более простой способ получения этого
результата: при φ=0 колебания от всех
зон в P приходят в одинаковой фазе,
поэтому результирующая амплитуда=сумме
амплитуд складываемых колебаний. При
│.
Для точки против линзы φ=0 -> Aφ=A0.
Более простой способ получения этого
результата: при φ=0 колебания от всех
зон в P приходят в одинаковой фазе,
поэтому результирующая амплитуда=сумме
амплитуд складываемых колебаний. При
 1,2,..) Aφ
обращается
в 0, значит данная формула определяет
положение минимумов интенсивности.
Модуль sinφ не превышает 1, значит
1,2,..) Aφ
обращается
в 0, значит данная формула определяет
положение минимумов интенсивности.
Модуль sinφ не превышает 1, значит
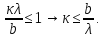 Если
разность хода от краев щели
Если
разность хода от краев щели
 ,
то открытая часть волновой пов-сти
разбивается на 2
,
то открытая часть волновой пов-сти
разбивается на 2 равных по ширине зон, разность хода
от краёв которых будет равна
равных по ширине зон, разность хода
от краёв которых будет равна
 .
Колебания от каждой пары соседних
зон взаимно погашают друг друга,
поэтому при
.
Колебания от каждой пары соседних
зон взаимно погашают друг друга,
поэтому при
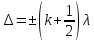 число зон будет нечётным и наблюдается
максимум интенсивности. Iφ=I0
число зон будет нечётным и наблюдается
максимум интенсивности. Iφ=I0 (I0-
интенсивность в центре дифракционной
картины). Из формулы вытекает, что
I-φ=Iφ,
значит картина симметрична относ.
центра линзы. При ширине щели, меньшей
длины волны, минимумы не возникают.
Краям центрального max соответствуют
значения φ, получающееся из bsinφ=±
(I0-
интенсивность в центре дифракционной
картины). Из формулы вытекает, что
I-φ=Iφ,
значит картина симметрична относ.
центра линзы. При ширине щели, меньшей
длины волны, минимумы не возникают.
Краям центрального max соответствуют
значения φ, получающееся из bsinφ=± -> угловая ширина центрального max:
-> угловая ширина центрального max:
 .
При b>>
.
При b>> значение sin
значение sin =
=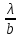 ->
->
 .
.
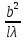 –параметр,
от которого зависит характер дифракции.
–параметр,
от которого зависит характер дифракции.
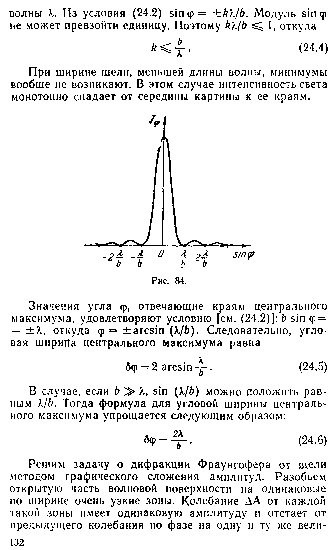
 , где
, где
 линейное расстояние на экране между
спектральн.линиями, различающимися
на
линейное расстояние на экране между
спектральн.линиями, различающимися
на
 При небольших
При небольших

 ,
где
,
где
 -
фокусное расстояние собирающей
линзы.->
-
фокусное расстояние собирающей
линзы.-> 
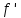 D
-> Dлин
=
D
-> Dлин
=
 . Разрешающая
сила: R=
. Разрешающая
сила: R= ,
где
,
где
 -
минимальная разность длин волн двух
спектральных линий, при которой они
воспринимаются раздельно. Возможность
разрешения двух спектр.линий зависит
от расстояния между ними и от ширины
спектрального максимума. 2 близких
max
воспринимаются глазом раздельно,
если интенсивность в промежутке между
ними- не более 80% от интенсивности
max.
Но такое соотношение возможно
если середина одного max
совпадает с краем другого. Положение
середины m-го max для длины волны
-
минимальная разность длин волн двух
спектральных линий, при которой они
воспринимаются раздельно. Возможность
разрешения двух спектр.линий зависит
от расстояния между ними и от ширины
спектрального максимума. 2 близких
max
воспринимаются глазом раздельно,
если интенсивность в промежутке между
ними- не более 80% от интенсивности
max.
Но такое соотношение возможно
если середина одного max
совпадает с краем другого. Положение
середины m-го max для длины волны
 :
dsinφmax=m(
:
dsinφmax=m( ,
для края m-го max для длины волны
,
для края m-го max для длины волны
 :
dsinφmax=(
:
dsinφmax=( ,
-> m(
,
-> m( (N-кол-во
щелей решётки)-> R=mN
(N-кол-во
щелей решётки)-> R=mN


 .
В случае, когда А1=А2
и
δ=
.
В случае, когда А1=А2
и
δ=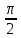 угол между направлениями векторов
угол между направлениями векторов
 и
и
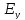 равен:
равен:
 ,
значит плоскость поляризации
поворачивается вокруг направления
луча с угловой скоростью, равной
частоте колебания
,
значит плоскость поляризации
поворачивается вокруг направления
луча с угловой скоростью, равной
частоте колебания
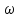 .
Поляризация в этом случае будет
круговой.
.
Поляризация в этом случае будет
круговой.
 или
или
 будет эллиптическая
поляризация, а при
будет эллиптическая
поляризация, а при
 или
π – эллипс вырождается в прямую –
такая поляризация называется
линейной(плоской)
или
π – эллипс вырождается в прямую –
такая поляризация называется
линейной(плоской)


 .
Для плоскополяризованного света
.
Для плоскополяризованного света
 ,
для естественного
,
для естественного

 отраженный свет становится полностью
поляризованным и его плоскость
поляризации становится перпендикулярной
плоскости падения:
отраженный свет становится полностью
поляризованным и его плоскость
поляризации становится перпендикулярной
плоскости падения:
 закон
Брюстера. Степень поляризации
отраженного и преломленного лучей
при различных углах падения можно
получить с помощью формул Френеля.
закон
Брюстера. Степень поляризации
отраженного и преломленного лучей
при различных углах падения можно
получить с помощью формул Френеля.
 в направлении оптической оси и в
направлениях, перпендикулярных к ней
имеет различные значения
в направлении оптической оси и в
направлениях, перпендикулярных к ней
имеет различные значения и
и
 .
.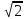 .(0.5).
Через поляризатор P’
пройдут составляющие колебаний E0
и Eе,
и их амплитуды в обоих случаях равны
(0.5) умноженным на cos(π/4),
те E'0=
E'e=Е/2(1)
.(0.5).
Через поляризатор P’
пройдут составляющие колебаний E0
и Eе,
и их амплитуды в обоих случаях равны
(0.5) умноженным на cos(π/4),
те E'0=
E'e=Е/2(1)

 ,
E'e||=E0cosφ=E
,
E'e||=E0cosφ=E .
Эти колеб.будут интерферировать и
ампл. E'||
результир. колеб.:
.
Эти колеб.будут интерферировать и
ампл. E'||
результир. колеб.:


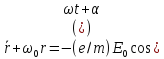

 cовпадают
с направлением
cовпадают
с направлением

 ,
поэтому геометрическое сложение
можно заменить алгебраическим)
,
поэтому геометрическое сложение
можно заменить алгебраическим)
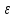 через
через
 получаем
получаем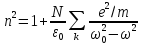


 .
Суперпозиция волн, мало отличающихся
друг от друга по частоте, называется
волновым
пакетом
или группой
волн.
Аналитическое выражение для группы
волн:
.
Суперпозиция волн, мало отличающихся
друг от друга по частоте, называется
волновым
пакетом
или группой
волн.
Аналитическое выражение для группы
волн:
 ,
то относительное расположение волн
остается неизменным и центр также
будет перемещаться с той же скоростью.
,
то относительное расположение волн
остается неизменным и центр также
будет перемещаться с той же скоростью.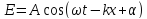

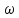 .
Суперпозиция волн, мало отличающихся
друг от друга по частоте, называется
волновым
пакетом
или группой
волн.
Аналитическое выражение для группы
волн:
.
Суперпозиция волн, мало отличающихся
друг от друга по частоте, называется
волновым
пакетом
или группой
волн.
Аналитическое выражение для группы
волн:
 ,
то относительное расположение волн
остается неизменным и центр также
будет перемещаться с той же скоростью.
,
то относительное расположение волн
остается неизменным и центр также
будет перемещаться с той же скоростью.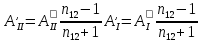 ;
;
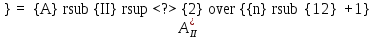 ;
;


 имеет промежуточные значения.
Следовательно, из анизотропии
имеет промежуточные значения.
Следовательно, из анизотропии
 вытекает, что электромагнитным волнам
с различным направлением колебаний
вектора напряженности Е
соответствуют
различные значения показателя
преломления n,
что означает зависимость скорости
волны от направления колебания
вытекает, что электромагнитным волнам
с различным направлением колебаний
вектора напряженности Е
соответствуют
различные значения показателя
преломления n,
что означает зависимость скорости
волны от направления колебания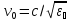

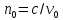

 или
или
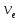 ,
различают положительные
(рис.2,
,
различают положительные
(рис.2,


 )
и отрицательные
(рис.3, ,
)
и отрицательные
(рис.3, ,
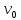

 )
одноосные
кристаллы
)
одноосные
кристаллы Рис.2
Рис.3
Рис.2
Рис.3 – собственная частота
– собственная частота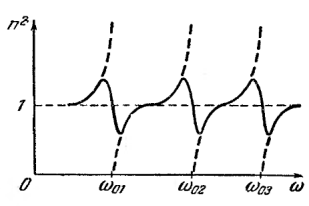


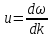
 заменит через
заменит через
 то, выражение групповой скорости
представляется в виде
то, выражение групповой скорости
представляется в виде
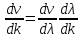
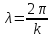 следует, что
следует, что
 ,
отсюда
,
отсюда
 ,
подставляя в выражение для групповой
скорости, получим
,
подставляя в выражение для групповой
скорости, получим

 заменит через
заменит через
 то, выражение групповой скорости
представляется в виде
то, выражение групповой скорости
представляется в виде

 следует, что
следует, что
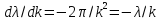 ,
отсюда
,
отсюда
 ,
подставляя в выражение для групповой
скорости, получим
,
подставляя в выражение для групповой
скорости, получим


 ,
т.е. большее на некоторое добавочное
время, равное
,
т.е. большее на некоторое добавочное
время, равное
 .
Учитывая добавочное время, заменим
t
на t-
.
Учитывая добавочное время, заменим
t
на t-



 – интенсивность на границе света на
входе в поглощающий слой,
– интенсивность на границе света на
входе в поглощающий слой,
 – толщина слоя,
– толщина слоя,
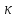 – коэффициент
поглощения (величина,
обратная толщине слоя, при прохождении
которого интенсивность уменьшается
в е
раз).
– коэффициент
поглощения (величина,
обратная толщине слоя, при прохождении
которого интенсивность уменьшается
в е
раз).
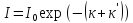
 - коэффициент
экстинкции
- коэффициент
экстинкции