4.Правило Крамера (вывод формул…)

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных, называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

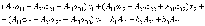Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Далее рассмотрим коэффициенты при x₂: Аналогично можно показать,

что и

Наконец несложно заметить, что

Таким образом, получаем равенство:

Следовательно,

Аналогично выводятся равенства и, откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

5.Матрицы. Действие над ними, обратная матрица. Ранг матрицы.

Матрица – множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Для обозначения матрицы используется надпись:

a_ij, I – номер строки, j – номер столбца.

Элементы матрицы, стоящие на диагонали, идущие из верхнего левого угла называют главной диагональю, другую диагональ называют побочной.

Если количество строк m матрицы не равно количеству столбцов n, то матрица называется прямоугольной.

Если количество столбцов матрицы совпадают с количеством строк, то матрица называется квадратной .

Количество строк или столбцов в квадратной матрице называются ее порядком.

Если все элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной .

Если все числа главной диагонали равны единице, то матрица называется единичной .

Если в прямоугольной матрице m*n m=1, то получается матрица-строка.

Если n=1, то получается матрица-столбец .

Матрицы-строки матрицы-столбцы называются векторами.

Свойства матриц:

A + (B + C) = (A + B) + C

A + B = B + A

A(BC) = (AB) C

A (B + C) = AB + AC

(B + C) A = BA + CA

(AT) T = A

(A * B) T = BT * AT

Действия с матрицами

Сложение матриц

Матрицы одинакового размера можно складывать.

Суммой двух таких матриц А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В. Символически будем записывать так: А+В=С.

Произведением матрицы А на матрицу В называется матрица С=АВ.

Правила умножения прямоугольных матриц:

Умножение матрицы А на матрицу В имеет смысл в том случае, когда число столбцов матрицы А совпадает с числом строк в матрице В.

В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк было в первой матрице и столько столбцов, сколько столбцов было во второй матрице.

Умножение матрицы на число

При умножении матрицы A на число a 2A5 G8A;0, A>AB02;ONI85 <0B@8FC A, C<=>60NBAO =0 G8A;> a. 0?@8<5@, C<=>68< <0B@8FC =0 G8A;> 2. @8 C<=>65=88 <0B@8FK =0 G8A;> <=>68B5;L «2=>A8BAO» ?>4 7=0: <0B@8FK.

Транспонирование матрицы

Транспонированная матрица – матрица A^Т, полученная из исходной матрицы A заменой строк на столбцы.

Формально, транспонированная матрица для матрицы A размеров m*n – матрица A^T размеров n*m, определённая как A^T[i, j] = A [j, i].

Например,

Свойства транспонированных матриц

1. (A^T)^T = A

2. (A + B)^T = A^T + B^T

3. (AB)^T = B^TA^T

4. detA = detA^T

Обратная матрица.

Обра́тная ма́трица — такая 09001108100000105000108000%матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате 004080081000180001108100единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её 09010504050081050180001108118определитель не равен нулю. Для неквадратных матриц и 018100604050000180001108100вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести 09105020400011001000180001108100%09105020400011001000180001108100%%22%22псевдообратныеHYPERLINK%20%22http://ru.wikipedia.org/wiki/%D0%9F%D1%81%D0%B5%D0%B2%D0%B4%D0%BE%D0%BE%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0%22%20матрицы%22%20матрицы"псевдообратныеHYPERLINK "20матрицы%22псевдообратныеHYPERLINK%20%22%22псевдообратныеHYPERLINK%20%22http://ru.wikipedia.org/wiki/%D0%9F%D1%81%D0%B5%D0%B2%D0%B4%D0%BE%D0%BE%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D0%B0%D1%8F_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0%22%20матрицы%22%20матрицы" матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы.

· , гдеобозначает 0901050405008105018определитель.

· для любых двух обратимых матрици.

· гдеобозначает транспонированную матрицу.

· для любого коэффициента.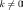

· Если необходимо решить 01081105000008005090181000030501100081051008111000200500809систему линейных уравнений , (b — ненулевой вектор) где— искомый вектор, и еслисуществует, то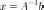. В противном случае либо размерность 090800509000501011100011020пространства решений больше нуля, либо их нет вовсе

Определение ранга матрицы.

Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение

Вычисление ранга матрицы с помощью миноров

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.

Пример 1. Найти методом окаймления миноров ранг матрицы

.

Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М₁ = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M₂ = , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М₂. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их: = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

Вычисление ранга матрицы с помощью элементарных преобразований

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю,  например,

.

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Пример 2 Найти ранг матрицы

А=

и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

.

 Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

; из третьей строки вычтем первую; получим матрицу

В = , которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

.