32.Эллипсоиды. Эллипсоид вращения. Сфера.

Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением

где a,  b,  c>0 — параметры эллипсоида. Это уравнение называется каноническим уравнением эллипсоида, а система координат, в которой эллипсоид описывается каноническим уравнением, называется канонической.

Эллипсо́ид враще́ния (сферо́ид) — это фигура вращения в трехмерном пространстве, образованная при вращении эллипса вокруг одной из его главных осей.

Эллипсоид вращения является частным случаем эллипсоида, две из трёх полуосей которого имеют одинаковую длину ():

• Вытянутый эллипсоид вращения

Вытянутый эллипсоид вращения можно также определить как геометрическое место точек пространства, для которых сумма расстояний до двух заданных точек (фокусов) постоянна.

Зеркало в виде вытянутого эллипсоида вращения обладает следующим свойством: лучи света, исходящие из одного из фокусов эллипсоида, после отражения соберутся в другом фокусе.

Сплюснутый эллипсоид вращения

Сплюснутый эллипсоид вращения можно также определить как геометрическое место точек пространства, для которых сумма расстояний до ближайшей и до наиболее удалённой точки заданной окружности постоянна.

Сферой называется геометрическое место точек (множество точек) пространства, удаленных от данной точки, называемой центром, на данное положительное расстояние, называемое радиусом. Радиусом сферы называют также любой F--9D0отрезок, один конец которого --- центр сферы, а второй лежит на сфере.

Площадь сферы

Объем шара, ограниченного сферой

Площадь сегмента сферы

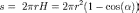, где H — высота сегмента, а  — зенитный угол

33.

Гиперболоид (от др.-греч. ὑπερβολή — гипербола, и εἶδος — вид, внешность). В математике гиперболоид — это вид поверхности второго порядка в трёхмерном пространстве.  однополосный и двухполосный 

  (однополостный гиперболоид),

где a и b — действительные полуоси, а c — мнимая полуось;

или

  (двуполостный гиперболоид),

где a и b — мнимые полуоси, а c — действительная полуось.

Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двухполостный — вокруг действительной. Двуполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: . В этом случае A и B называются фокусами гиперболоида.

Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.

34. Параболоиды и канонические поверхности.

Параболоиды

Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка.

Канонические уравнения параболоида в декартовых координатах:

Если а и b одного знака, то параболоид называется эллиптическим.

Если a и b разного знака, то параболоид называется гиперболическим.

если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром.

Гиперболический параболоид

Канонические уравнения поверхностей второго порядка

Поверхность второго порядка задается в декартовых координатах уравнением второй степени

Ax2+By2+Cz2+2Dxy+2Exz+2Fyz+2Gx+2Hy+2Kz+L=0.

За счет выбора специальной системы координат это уравнение преобразуется к простейшему (каноническому) виду.

Цилиндрические поверхности:

г) – эллипсоид;

д) – двуполостный гиперболоид;

е) – однополостный гиперболоид;

ж) – эллиптический параболоид.