27. Расстояние от точки до прямой в пространстве (вывод формулы). Расстояние между параллельными прямыми в пространстве.

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

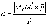Если s(p) = {m; n; p} - направляющий вектор прямой l, M₁(x₁, y₁, z₁) - точка лежащей на прямой, тогда расстояние от точки M₀(x₀, y₀, z₀) до прямой l можно найти, используя формулу

Вывод формулы

Если задано уравнение прямой l то несложно найти s(p) = {m; n; p} - направляющий вектор прямой и M₁(x₁, y₁, z₁) - координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах

S = |M₀M₁×S(p)|.

С другой стороны площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне

S = |s|d.

В нашем случае высота будет равна расстоянию от точки до плоскости d, а сторона параллелограмма равна модулю направляющего вектора s.

Приравняв площади несложно получить формулу расстояния от точки до прямой.

Расстояние между параллельными прямыми в пространстве

Можно найти расстояние между прямыми в пространстве как расстояние между плоскостями.

Расстояние между двумя параллельными плоскостями — равно длине перпендикуляра, опущенного из точки одной плоскости на другую плоскость.

Если заданы уравнения параллельных плоскостей A_x + B_y + C_z + D₁ = 0 и A_x + B_y + C_z + D₂ =0, то расстояние между плоскостями можно найти, используя следующую формулу

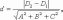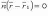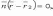а если уравнениями ито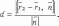

28.Определение эллипса и вывод канонического уравнения.

Каноническое уравнение эллипса

Эллипсом – называется геометрическое место точек на плоскости, сумма расстояний которых до двух заданных точек, называемых фокусами, есть, величина постоянная, большая чем расстояние между фокусами.

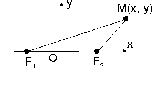
Комментарии к определению: F1 и F2 – фокусы, | F1F2 | = 2·с — расстояние между фокусами, | MF1 | + |MF2| = 2·a >2·c — определение эллипса.

Система координат, в которой уравнение имеет наиболее простой вид, называется канонической. Проведём ось абсцисс через фокусы, начало координат поместим в середине между фокусами, ось ординат направим перпендикулярно. Пусть М(х, у) — произвольная точка на эллипсе, тогда F1(- c; 0) и F2(c; 0). Расстояния текущей точки эллипса до её фокусов называются фокальными расстояниями |MF1| = r1, |MF2| = r2 и, по определению эллипса, имеем r1 + r2 = 2·a.

Воспользовавшись формулой расстояния между двумя точками, из определения эллипса имеем:

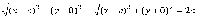
Избавимся от иррациональности, возведя обе части соотношения

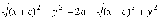
в квадрат:

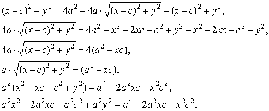
далее

Разделив обе части последнего соотношения на a2b2, получим каноническое уравнение эллипса

Исследование формы эллипса

Так как

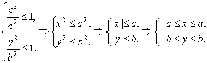
то эллипс лежит внутри прямоугольника со сторонами х = ± а, у = ± b.

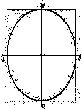
Эллипс является симметричным относительно начала координат и относительно осей координат. Это следует из-за того, что в уравнении эллипса переменные x и y входят квадратами x2, y2. Если уравнению эллипса удовлетворяет точка с координатами x и y, то уравнению эллипса будут удовлетворять точки с координатами ( −x, − y), (− x, y), (x, − y).

Фокусы эллипса лежат на его большой оси эллипса.

Соотношения для фокальных расстояний эллипса

Убедимся в том, что если координаты точки удовлетворяют каноническому уравнению эллипса, то сумма расстояний этой точки до двух точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Для этого, очевидно, достаточно показать, что величины r1 и r2 для любой точки, координаты которой удовлетворяют уравнению эллипса, удовлетворяют соотношению r1 + r2= 2·a.

Найдём из уравнения эллипса

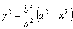
и подставим это выражение в соотношение

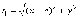
Получим

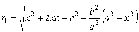
После преобразования получим соотношение для фокального радиуса

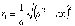
Так как по определению с < a и | х | < a, то выражение в скобках под знаком корня положительно, поэтому

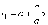
Аналогично найдём

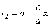
Складывая фокальные расстояния, получим r1 + r2 = 2·a

Что и требовалось доказать. Таким образом, эллипс — линия второго порядка.

Замечание. Если а = b, то уравнение эллипса принимает вид x2 + y2= a2. Это уравнение окружности радиуса а. Таким образом, окружность — частный случай эллипса. Заметим, что эллипс можно получить из окружности радиуса а, если сжать ее в а ⁄ b раз вдоль оси Оу.

Оси симметрии эллипса называются его осями, а центр симметрии (точка пересечения осей) — центром эллипса. Точки, в которых эллипс пересекает оси, называются его вершинами. Вершины ограничивают на осях отрезки, равные 2·а и 2·b. Если а ≥ b, величины а и b называются соответственно большой и малой полуосями эллипса.

Эксцентрисит эллипса

Определение. называется отношение c ⁄ a, где с — половина расстояния между фокусами, а — большая полуось эллипса.

Эксцентриситет обозначают буквой ε: ε = c⁄ a. Так как ε = с ⁄ a, то 0 ≤ ε ≤ 1. Принимая во внимание, что ε2 = с2 ⁄ a2 = ( a2 – b2) ⁄ a2 = 1 – (a ⁄ b)2, получим

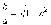
Из последнего равенства легко получается геометрическое истолкование эксцентриситета эллипса. При очень малом ε числа а и b почти равны, т.е. эллипс близок к окружности. Если же ε близко к единице, то число b весьма мало по сравнению с числом а и эллипс сильно вытянут вдоль большой оси. Таким образом, эксцентриситет эллипса характеризует меру вытянутости эллипса. Соотношения для фокальных радиусов для эллипса примут вид

r1 = a + ε·x, r2 = a - ε·x

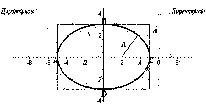
Директрисы эллипса

Определение. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии а⁄ ε от него, называются директрисами эллипса (здесь, а — большая полуось, ε — эксцентриситет эллипса).

Так как для эллипса ε < 1, то a ⁄ ε > a. Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая — общее свойство, присущее эллипсу.

Теорема. Если r1 — фокальное расстояние произвольной точки М эллипса до какого-нибудь фокуса, d — расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r1 ⁄d есть постоянная величина, равная эксцентриситету эллипса.

Д о к а з а т е л ь с т в о. Предположим для определенности, что речь идет о правом фокусе F1 и правой директрисе. Пусть М (х; у) — произвольная точка эллипса. Расстояние от точки М до правой директрисы выражается равенством

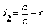
Кроме того, r2 = a - ε·x

Составляя отношение, получим

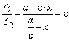
Аналогично доказывается для левого фокуса эллипса.