
- •1. Определение 2-ого и 3-его порядка. Решение систем 2х и 3х линейных уравнений с двумя и тремя неизвестными.
- •2. Алгебраические дополнения и миноры. Основные свойства определителей. Определители n-го порядка.
- •3. Различные способы вычисления определителей 3-го порядка
- •4.Правило Крамера (вывод формул…)
- •5.Матрицы. Действие над ними, обратная матрица. Ранг матрицы.
- •6. Матричная запись системы линейных уравнений. Решение с помощью обратной матрицы.
- •7.Исследование систем m линейных уравнений c n неизвестными. Метод Гаусса.
- •8. Система линейных однородны уравнений. Теорема о ненулевых решениях таких систем (доказать).
- •9.Система координат на прямой, плоскости и в пространстве. Уравнение линии на плоскости.
- •10.Простейшие задачи аналитической геометрии. Деление отрезка в данном отношении. Расстояние между точками (вывод формул).
- •11.Векторы. Направляюшие косинусы. Проекция вектора на вектор. Длина вектора. Коллинеарность, ортогональность, компланарность векторов.
- •Проекция вектора на вектор.
- •12.Линейные операции над векторами. Сложение, вычитание и умножение вектора на число.
- •13.Вывод формулы для вычисления скалярного произведения через координаты перемножаемых векторов. Свойства.
- •14.Векторное произведение. Координаты вектора векторного произведения. Его свойства. Условия колинеарности.
- •15.Приложение векторного произведения: площадь треугольника в пространстве и на плоскости через координаты его вершин.
- •16.Смешанное произведение. Вывод формулы объема параллелепипеда.
- •17. Cвойства смешенного произведения. Вывод формулы объема пирамиды и ее высоты. Условия принадлежности 4 точек к одной плоскости . Условия комплонарности 3 векторов.
- •18. Различные уравнения прямой на плоскости(наклонной,через две точки, общее, каноническое,параметрическое).
- •21.Различные уравнения плоскости (общее, уравнение плоскости проходящей через 3 точки уравнение плоскости в отрезках).
- •23. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей. Расстояние между двумя параллельными плоскостями.
- •24. Различные уравнения прямой в пространстве. Переход от общих уравнений к каноническим и обратно.
- •25. Взаимное расположение прямой и плоскости
- •26. Угол между прямой и плоскостью. Точка пересечения между прямой и плоскостью.
- •27. Расстояние от точки до прямой в пространстве (вывод формулы). Расстояние между параллельными прямыми в пространстве.
- •28.Определение эллипса и вывод канонического уравнения.
- •29. Определение гиперболы и вывод канонического уравнения.
- •30.Определение параболы и вывод канонического уравнения.
- •31.Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
- •32.Эллипсоиды. Эллипсоид вращения. Сфера.
- •34. Параболоиды и канонические поверхности.
- •35.Цилиндрической называется поверхность,
- •36. Ко́мпле́ксные чи́сла
- •1. 2.3..
- •1. . 2.. 3..
25. Взаимное расположение прямой и плоскости
Угол между прямыми. Угол между прямой и плоскостью
Определение. Углом между прямыми в пространстве называют любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Угол
между прямыми в пространстве равен углу
между их направляющими векторами  .Поэтому,
если две прямые заданы каноническими
уравнениями вида
.Поэтому,
если две прямые заданы каноническими
уравнениями вида 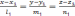 и
и 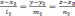 то
косинус угла между ними можно найти по
формуле:
то
косинус угла между ними можно найти по
формуле:
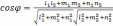 ).
).
Пример.
Найти угол между прямыми 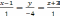 и
и 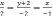 .
.
Решение.
По условию  ,тогда
,тогда
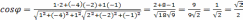 отсюда
отсюда
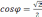 ,
,  ,
,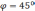 .
.
Условия параллельности и перпендикулярности прямых
Условия
параллельности и перпендикулярности
двух прямых равносильны условиям
параллельности и перпендикулярности
их направляющих векторов  .
.
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:
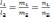 –
условие
параллельности прямых.
–
условие
параллельности прямых.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:
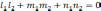 –
условие
перпендикулярности прямых.
–
условие
перпендикулярности прямых.
Пример.
Найти уравнения прямой проходящей через
точку 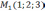 параллельно
прямой
параллельно
прямой 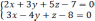 .
.
Решение. Поскольку искомая прямая параллельна данной прямой, то в качестве направляющего вектора искомой прямой можно взять направляющий вектор данной прямой.
По
условию 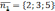 ,
,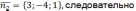
 –
отсюда
уравнение искомой прямой имеет вид:
–
отсюда
уравнение искомой прямой имеет вид: 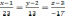 .
.

Угол между прямой, заданной каноническими уравнениями и плоскостью, определяемой общим уравнением
|
|
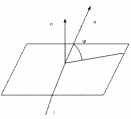
Определение. Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Пусть
прямая задана каноническими
уравнениями Рассмотрим
векторы Если угол между ними острый, то он будет Если
угол между векторами |
Следовательно 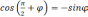 .Поэтому
в любом случае
.Поэтому
в любом случае  .Применив
формулу вычисления косинуса угла между
векторами, получим
.Применив
формулу вычисления косинуса угла между
векторами, получим 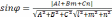 .
.
Условия параллельности и перпендикулярности прямой и плоскости
Пусть
прямая задана каноническими уравнениями 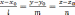 ,а
плоскость общим уравнением
,а
плоскость общим уравнением 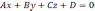 .
.
Прямая
и плоскость параллельны тогда и только
тогда, когда направляющий вектор
прямой 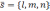 и
нормальный вектор плоскости
и
нормальный вектор плоскости 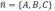 перпендикулярны,
то есть их скалярное произведение равно
нулю
перпендикулярны,
то есть их скалярное произведение равно
нулю 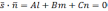 –условие
параллельности прямой и плоскости
–условие
параллельности прямой и плоскости
Прямая
и плоскость перпендикулярны тогда и
только тогда, когда направляющий вектор
прямой  и
нормальный вектор
и
нормальный вектор  плоскости
коллинеарны
плоскости
коллинеарны 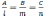 –условие
перпендикулярности прямой и плоскости.
–условие
перпендикулярности прямой и плоскости.
Пример.
Найти угол между прямой 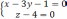 и
плоскостью
и
плоскостью 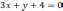 .
.
Решение.
По условию 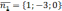 ,
,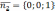 ,тогда
,тогда 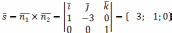 .
.
Из
уравнения плоскости имеем, что нормальный
вектор 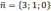 .Следовательно
.Следовательно 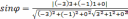 =
=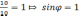 Þ
Þ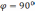 .
.
26. Угол между прямой и плоскостью. Точка пересечения между прямой и плоскостью.
Угол
между прямой и плоскостью.
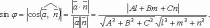
Точка пересечения прямой с плоскостью.
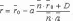
Если две прямые лежат в одной плоскости, угол между ними легко измерить — например, с помощью транспортира. А как измерить угол между прямой и плоскостью?
Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.
Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.
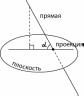
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол.
Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.
Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Это определение. Но как же с ним работать? Как проверить, что данная прямая перпендикулярна всем прямым, лежащим в плоскости? Ведь их там бесконечно много.
На практике применяется признак перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
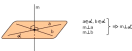

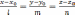 ,а
плоскость общим уравнением
,а
плоскость общим уравнением 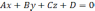 .
. и
и  .
.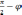 ,
а
,
а 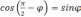 .
. и
и  тупой,
то он равен
тупой,
то он равен 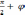 .
.