Поток нейтронов

При взаимодействии нейтронов с ядрами среды основное внимание уделяется расчету скоростей процессов разного типа. Скорость процесса есть число актов определенного типа взаимодействия нейтронов с ядрами среды. Для ее вычисления наряду с характеристиками ядер среды необходимо знать характеристики ансамбля нейтронов, взаимодействующих с ядрами среды. Таким характеристиками являются плотность нейтронов , которая равна числу нейтронов, обладающих определенными характеристиками (энергией и направлением движения ) в единице объема размножающей среды и плотность потока нейтронов, или просто поток нейтронов . В размножающих средах нейтроны различаются как энергией , так и направлением движения и поэтому в каждой точке активной зоны для каждого направления движения будет свой поток нейтронов типа . Для нейтронов определенного направления движения понятие потока нейтронов такое же, как мы определили выше. В подавляющем большинстве случаев интенсивность взаимодействия нейтронов с ядрами среды не зависит от направления движения нейтронов. Поэтому в реакторной физике используется интегральная величина - полный поток нейтронов

В этом случае под полным потоком нейтронов понимается число нейтронов, пересекающих единичную площадку любой ориентации, в единицу времени, то есть предполагается изотропное распределение нейтронов в каждой точке активной зоны.

Для понимания величины потока нейтронов рассмотрим простой пример взаимодействия нейтронов с ядрами среды, когда у нас имеется моноэнергетический источник нейтронов, направление скорости которых одинаковы. Пусть этот ансамбль нейтронов налетает на мишень в виде плоской пластины, перпендикулярно к ее поверхности (Рис.3).

Рис. 3. Прохождение пучка нейтронов через образец

Под потоком нейтронов в этом случае будем понимать число нейтронов, пересекающих единичную площадку мишени в единицу времени. За 1 сек. пересечь единичную площадку могут только те нейтроны, которые находятся от нее на расстояние, проходимое нейтронами за это время. Следовательно, поток нейтронов будет равен

где -плотность нейтронов источника. Подсчитаем интенсивность взаимодействия нейтронов с ядрами среды. Расстояния между ядрами в среде столь велико по сравнению с поперечными размерами ядер, что ядра в пластине не затеняют друг друга. Если пучок нейтронов падает на пластину, площадью и толщиной 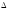, то полное число взаимодействий нейтронов с ядрами среды в единицу времени будет

где вероятность падающему на пластину нейтрону осуществить взаимодействие с ядрами среды. Это вероятность можно представить как отношение площади, образованной поперечными сечениями всех ядер пластины к полной площади пластины . Полная площадь, покрываемая ядрами , где - число ядер в единице объема пластины или ядерная концентрация, а - микроскопическое поперечное сечение ядра для падающих на пластину нейтронов. В результате получим

Плотность взаимодействий есть число актов взаимодействия нейтронов в единице объема в единицу времени

.

Величина носит название макроскопического сечения взаимодействия, так что . Это соотношение имеет большое значение в физике реакторов. Оно показывает, что плотность взаимодействия нейтронов с веществом зависит как от самого вещества через макроскопическое сечение , так и от интенсивности пучка падающих нейтронов через поток нейтронов 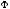. При подстановке в эту формулу макросечения деления , мы получим распределение плотности энерговыделения по активной зоне. Именно это и объясняет важность расчета пространственного распределения потока нейтронов разных энергий по всему объему активной зоны.

Цепной процесс размножения нейтронов

Основные понятия цепного процесса

Тот факт, что при делении ядер, осуществляемого нейтронами, появляются вторичные нейтроны как продукты реакции деления, позволяет осуществлять цепной процесс деления в среде, содержащей делящиеся ядра. Такие среды в дальнейшем будем называть размножающими, поскольку в них возможен самоподдерживающийся процесс воспроизводства нейтронов. Поскольку для делящихся ядер число вторичных нейтронов на один поглощенный в ядерной реакции, то есть величина , то цепной процесс деления может носить стационарный характер с выделением большого количества энергии в течение длительного времени.

При рассмотрении цепных процессов все нейтроны в размножающей среде в любой момент времени можно разделить на отдельные поколения. Нейтрон каждого поколения, участвующий в цепном процессе деления в активной зоне реактора, проходит следующий жизненный цикл:

• рождается в реакции деления,

• некоторое время движется в активной зоне, рассеиваясь на ядрах среды (замедляется и диффундирует),

• затем либо порождает новый акт деления и нейтроны следующего поколения, либо теряется без порождения новых нейтронов, например в реакции радиационного захвата, либо покидает пределы размножающей среды.

Рис. 3 Цепной процесс деления

Модель сменяющихся поколений

Вначале рассмотрим упрощенную модель цепного процесса. Во-первых, размножающая среда представляется бесконечной, однородной и изотропной. Во-вторых, всем нейтронам в среде приписывается одна и та же энергия (так называемая односкоростная модель). В-третьих, предполагается, что все нейтроны каждого поколения рождаются одновременно, живут определенное время  (время жизни одного поколения) и одновременно заканчивают свой жизненный цикл, порождая нейтроны следующего поколения. В однородной и бесконечной среде все единичные объемы среды равноправны. Поэтому для описания нейтронов каждого поколения воспользуемся функцией плотности нейтронов, которая определяется как число нейтронов в единице объема.

Изотропность среды и использование односкоростной модели позволяет считать все нейтроны равноправными с точки зрения нейтронно-ядерных процессов в среде. Для такой модели цепного процесса введем понятие коэффициента размножения нейтронов , как отношение числа нейтронов последующего поколения к числу нейтронов предыдущего поколения в каждом единичном объеме среды :

.

Коэффициент размножения определяет характер поведения нейтронной плотности в размножающей среде. Для выбранной модели изменение во времени плотности нейтронов будет описываться кусочно-постоянной функцией времени

Однако если время жизни поколения мало, а коэффициент размножения не сильно отличается от единицы, временное поведение плотности нейтронов можно описать непрерывной функцией времени. Пусть в момент времени плотность нейтронов в среде была равна , тогда через промежуток времени, равный времени жизни поколения , в соответствии с определением коэффициента размножения их число будет увеличено в раз:

Рассмотрим приращение числа нейтронов за время жизни одного поколения :

Если мало, то приращение можно представить через производную функции плотности потока :

Таким образом, получилось непрерывное уравнение для временного изменения плотности нейтронов в размножающей среде – эволюционное уравнение :

Решением этого уравнения является экспоненциальная функция, показатель которой зависит от коэффициента размножения и от времени жизни поколения:

Очевидно, что при получим , то есть, в такой размножающей среде будет осуществляться стационарный процесс смены нейтронных поколений, а сама размножающая среда называется критической. Если же , то функция будет затухающая, и в этом случае говорят, что данная размножающая среда подкритическая. В противоположном случае, когда , будет возрастающей функцией, а сама размножающая система называется надкритической.

Рассмотрим случай, когда в среде присутствует внешний источник нейтронов постоянной мощности, не связанный с реакцией деления в среде. Предположим, что этот источник распределен равномерно по объему среды и порождает нейтронов в единицу времени в единице объема. В этом случае уравнение для плотности нейтронов в среде будет иметь вид :

.

Как известно, общее решение неоднородного дифференциального уравнения представляется в виде суммы двух слагаемых , где – общее решение однородного уравнения, а – частное решение неоднородного уравнения .

Следовательно, общее решение уравнения будет иметь вид.

Для критической размножающей среды и число нейтронов в единице объема будет изменяться по линейному закону 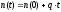, то есть в критической среде с внешним источником стационарный режим работы невозможен. Очевидно, что и в надкритической среде число нейтронов в единичном объеме также будет возрастать со временем, но уже по экспоненциальному закону. Однако если размножающая среда подкритическая , то в ней можно осуществить стационарный процесс, поскольку выражение для имеет асимптотическое стационарное решение , причем полное число нейтронов в единице объема среды зависит как от мощности внешнего источника , так и от степени близости коэффициента размножения к единице. Величина носит название коэффициента умножения мощности источника. Именно на этом принципе основано действие подкритических систем с внешним источником, в качестве которого рассматриваются ускорители протонов.

Модель последовательных поколений

Естественно, что в любой размножающей среде одновременно присутствуют нейтроны разных поколений и поэтому модель сменяющихся поколений не имеет большого практического значения. Рассмотрим общий случай, предположив, что в начальный момент времени в каждый единичный объеме размножающей среды было впущено нейтронов. Будем считать их нейтронами первого поколения. Рассмотрим развитие цепного процесса от поколения к поколению, при этом под поколением нейтронов понимаются все нейтроны, рожденные от нейтронов предыдущего поколения. В рамках односкоростной модели одногрупповые макроконстанты во всех поколениях будут также одинаковыми. Плотность нейтронов каждого поколения будет меняться со временем. Временное поведение нейтронов нулевого поколения будет удовлетворять уравнению.

(1)

Часть нейтронов нулевого поколения вызовет деление ядер среды, что и даст начало следующему поколению – . Для нейтронов первого поколения уравнение временного изменения их плотности в среде имеет вид

(2)

В общем случае, для произвольного i-го поколения нейтронов можно записать аналогичное уравнение:

(3)

Каждое поколение объединяет все нейтроны от момента их рождения до момента исчезновения (поглощения), и каждое новое поколение служит источником следующего. Временное поведение различных поколений нейтронов представлено на рисунке 4.

Рис. 2.1 Последовательные поколения нейтронов

Полное число нейтронов в каждом поколении будет равно интегралу по времени от источника этих нейтронов . Проинтегрируем каждое уравнение для плотности нейтронов в поколении по времени в интервале (0,) и введем в рассмотрение интегральную по времени плотность нейтронов в каждом поколении .

Запишем соотношения для последовательных поколений нейтронов :

По определению коэффициент размножения есть отношение общего числа нейтронов в двух последовательных поколениях . Учитывая полученные выше соотношения, запишем:

.

В результате получим выражение для коэффициента размножения в бесконечной размножающей среде.

Таким образом, в итоге мы получили выражение для коэффициента размножения в бесконечной размножающей среде. Физический смысл полученного результата заключается в том, что коэффициент размножения есть отношение скорости рождения нейтронов к скорости их поглощения. Отметим два важных следствия из полученных соотношений. Во-первых, отношение интегральных потоков нейтронов для двух последовательных поколений также равно коэффициенту размножения: . Во-вторых, баланс нейтронов для одного поколения выглядит следующим образом: . Физически это означает равенство количества рожденных нейтронов и количества поглощенных.

Усреднение макроконстант среды

В рассмотренной модели цепного процесса размножения нейтронов предполагалось, что все нейтроны в среде ничем не отличаются друг от друга. В реальной ситуации в размножающей среде в каждый момент времени присутствуют нейтроны разных поколений, причем и сами нейтроны различаются местоположением, энергией и направлением движения. В модели бесконечной однородной среды координата и направление движение нейтронов не влияют на скорость взаимодействия нейтронов. Существенным является то, что нейтроны каждого поколения различаются по энергиям, а энергия определяет скорость взаимодействия нейтронов с веществом.

В теории реакторов доказывается, что если рассматривать поколения с большими номерами, то есть если по временной шкале уйти далеко от начала цепного процесса, то независимо от энергетического распределения начального источника нейтронов, в бесконечной размножающей среде будет формироваться свой собственный спектр нейтронов, причем в каждом поколении он будет тем же самым. Это значит, что в асимптотике плотность нейтронов в каждом поколении будет зависеть от энергии однотипном образом

где - асимптотический спектр нейтронов в бесконечной размножающей среде. Исходя из нового определения коэффициента размножения, как отношения скоростей процессов рождения и поглощения нейтронов, запишем

Применяя обычную процедуру усреднения макрокостант, получим

усредненные макроконстанты среды, которые играют роль аналогичных констант среды в односкоростном приближении.