Основы программирования на языке Паскаль

1. Основные этапы решения задач на компьютере.

2. Основные элементы языка Паскаль.

3. Понятие алгоритма, свойства алгоритмов. Запись алгоритма в виде блок-схем.

4. Общая структура программы на Паскале. Алфавит языка. Данные целого и действительного типов (и действия над ними).

5. Описание переменных стандартных типов в Паскале. Стандартные функции в Паскале.

6. Арифметические выражения Паскаля. Оператор присваивания. Составной оператор.

7. Операторы ввода и вывода в Паскале.

8. Условный и составной операторы в Паскале.

9. Оператор цикла с параметром в Паскале.

10. Операторы цикла с предварительным условием, с последующим условием.

11. Массивы - как типы данных. Описание типов пользователя в Паскале.

12. Многомерные массивы. Нахождение минимального и максимального элемента массива.

13. Понятие файла. Чтение файла. Запись в файл.

14. Процедуры и функции в Паскале, определяемые пользователем.

15. Механизм передачи параметров в процедуры. Параметры-значения и параметры-переменные.

16. Область действия параметров. Локальные и глобальные переменные в Паскале.

17. Массивы в качестве параметров. Отличие процедур и функций.

18. Сортировка массива методом пузырька.

Основы программирования на языке Паскаль

1. Основные этапы решения задач на компьютере.

2. Основные элементы языка Паскаль.

3. Понятие алгоритма, свойства алгоритмов. Запись алгоритма в виде блок-схем.

4. Общая структура программы на Паскале. Алфавит языка. Данные целого и действительного типов (и действия над ними).

5. Описание переменных стандартных типов в Паскале. Стандартные функции в Паскале.

6. Арифметические выражения Паскаля. Оператор присваивания. Составной оператор.

7. Операторы ввода и вывода в Паскале.

8. Условный и составной операторы в Паскале.

9. Оператор цикла с параметром в Паскале.

10. Операторы цикла с предварительным условием, с последующим условием.

11. Массивы - как типы данных. Описание типов пользователя в Паскале.

12. Многомерные массивы. Нахождение минимального и максимального элемента массива.

13. Понятие файла. Чтение файла. Запись в файл.

14. Процедуры и функции в Паскале, определяемые пользователем.

15. Механизм передачи параметров в процедуры. Параметры-значения и параметры-переменные.

16. Область действия параметров. Локальные и глобальные переменные в Паскале.

17. Массивы в качестве параметров. Отличие процедур и функций.

18. Сортировка массива методом пузырька.

ПРОГРАММИРОВАНИЕ И ЧИСЛЕННЫЕ МЕТОДЫ

1. Решение трансцендентных уравнений. Основные этапы решения.

2. Приближенное решение уравнения f(x) = 0 методом деления пополам (метод бисекций). Условие сходимости метода. Оценка погрешности приближения корня при расчете на ЭВМ.

3. Метод простых итераций решения уравнения f(x) = 0. Достаточные условия сходимости метода. Оценка погрешности приближения корня при расчете на ЭВМ.

4. Численное интегрирование. Вывод квадратурной формулы для метода Симпсона. Оценка погрешности вычислений по правилу Рунге.

5. Приближенное интегрирование методом Гаусса. Оценка погрешности вычислений.

6. Решение систем линейных уравнений . Метод последовательных исключений переменных - метод Гаусса.

7. Аппроксимация функций, заданных дискретными (табличными) значениями, полиномом методом наименьших квадратов.

8. Аппроксимация линейной зависимостью и нелинейными функциями путем сведения к линейным.

9. Постановка одномерной задачи минимизации. Основные определения. Решение задачи одномерной оптимизации методом дихотомии (деления отрезка пополам).

10. Решение задачи одномерной минимизации на отрезке [ a, b ] методом золотого сечения.

ПРОГРАММИРОВАНИЕ И ЧИСЛЕННЫЕ МЕТОДЫ

1. Решение трансцендентных уравнений. Основные этапы решения.

2. Приближенное решение уравнения f(x) = 0 методом деления пополам (метод бисекций). Условие сходимости метода. Оценка погрешности приближения корня при расчете на ЭВМ.

3. Метод простых итераций решения уравнения f(x) = 0. Достаточные условия сходимости метода. Оценка погрешности приближения корня при расчете на ЭВМ.

4. Численное интегрирование. Вывод квадратурной формулы для метода Симпсона. Оценка погрешности вычислений по правилу Рунге.

5. Приближенное интегрирование методом Гаусса. Оценка погрешности вычислений.

6. Решение систем линейных уравнений 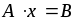. Метод последовательных исключений переменных - метод Гаусса.

7. Аппроксимация функций, заданных дискретными (табличными) значениями, полиномом методом наименьших квадратов.

8. Аппроксимация линейной зависимостью и нелинейными функциями путем сведения к линейным.

9. Постановка одномерной задачи минимизации. Основные определения. Решение задачи одномерной оптимизации методом дихотомии (деления отрезка пополам).

10. Решение задачи одномерной минимизации на отрезке [ a, b ] методом золотого сечения.