Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт космических и информационных технологий

институт

Информатика

кафедра

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1

_{ТЕМА: ЧИСЛЕННЫЕ МЕТОДЫ МНОГОМЕРНОЙ ОПТИМИЗАЦИИ}

КИ09-11

А. А. Егоров

Студент,

номер группы подпись, дата инициалы, фамилия

Н. А. Сергеева

Преподаватель

подпись, дата инициалы, фамилия

Красноярск 2012

СОДЕРЖАНИЕ

1 Постановка задачи 3

2 Теоретические сведения 5

2.1 Симплекс-метод 5

2.2 Метод покоординатного спуска нулевого порядка 6

2.3 Метод градиентного спуска с постоянным шагом 6

2.4 Метод наискорейшего градиентного спуска 7

3 Аналитическое решение уравнений 8

4 Исследование работы реализованных методов 9

4.1 Симплекс-метод 9

4.2Метод покоординатного спуска нулевого порядка 27

4.3 Метод градиентного спуска с постоянным шагом 31

4.4. Метод наискорейшего градиентного спуска 36

5 Выводы 42

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 43

1 Постановка задачи

Даны две двумерные функции:

;

;

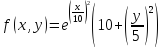1. Симплекс-метод

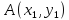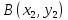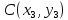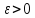Дано: Координаты трех вершин начального симплекса (,,), числодля остановки алгоритма, коэффициенты отражени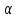я, сжатияи растяжения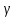, максимальное число итерацийN.

Необходимо найти безусловный минимум функции двух переменных, т. е. найти такую точку , с помощью симплекс-метода.

Реализовать и исследовать свойства данного метода.

2. Метод покоординатного спуска нулевого порядка

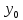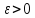Дано: начальные точки ,, числодля остановки алгоритма и максимальное число итерацийN.

Необходимо найти безусловный минимум функции двух переменных, т. е. найти такую точку 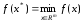, с помощью метода покоординатного спуска нулевого порядка.

Реализовать и исследовать свойства данного метода.

3. Метод градиентного спуска с постоянным шагом

Дано: начальные точки ,,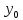 малые числа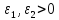для остановки алгоритма,N– предельное число итераций,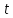– шаг.

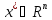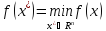Необходимо найти локальный минимум функции двух переменных на множестве допустимых решений, т. е. найти такую точку , чтос помощью метода градиентного спуска с постоянным шагом.

Реализовать и исследовать свойства данного метода.

4. Метод наискорейшего градиентного спуска

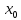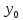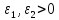Дано: начальные точки ,, малые числадля остановки алгоритма, М – предельное число итераций.

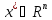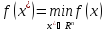Необходимо найти локальный минимум функции двух переменных на множестве допустимых решений, т. е. найти такую точку , чтос помощью метода градиентного спуска с постоянным шагом.

Реализовать и исследовать свойства данного метода.

2 Теоретические сведения

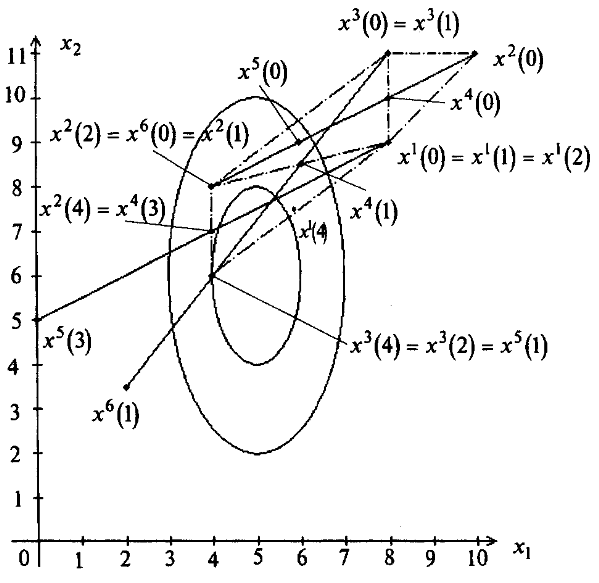
2.1 Симплекс-метод

Рисунок 1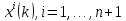

В основу метода деформируемого многогранника (метода Нелдера-Мида) положено построение последовательности системn+1 точек, которые являются вершинами выпуклого многогранника. Точки системы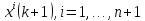на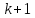итерации совпадают с точками системы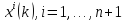, кроме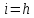, где точка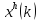– наихудшая в системе, т. е.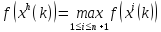. Точка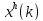заменяется на другую точку по специальным правилам. В результате многогранники деформируются в зависимости от структуры линий уровня целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума. Построение последовательности многогранников заканчивается, когда значение функции в вершинах текущего многогранника отличаются от значения функции в центре тяжести системы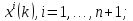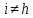не более чем на.

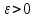2.2 Метод покоординатного спуска нулевого порядка

Рисунок 2

Метод покоординатного спуска нулевого порядка является классическим итерационным методом решения системы линейных уравнений. Стратегия решения задачи состоит в построении такой последовательности точек, что значение функции в каждой последующей точке меньше чем в предыдущей. Точки последовательности вычисляются по следующему правилу: фиксируется одна из переменных, затем минимизируя получившуюся функцию получаем значения для второй переменной, шаг повторяется пока не достигается заданная точность.