Расчёты по 1 части-ПРОСТОЕ СОПРОТИВЛЕНИЕ

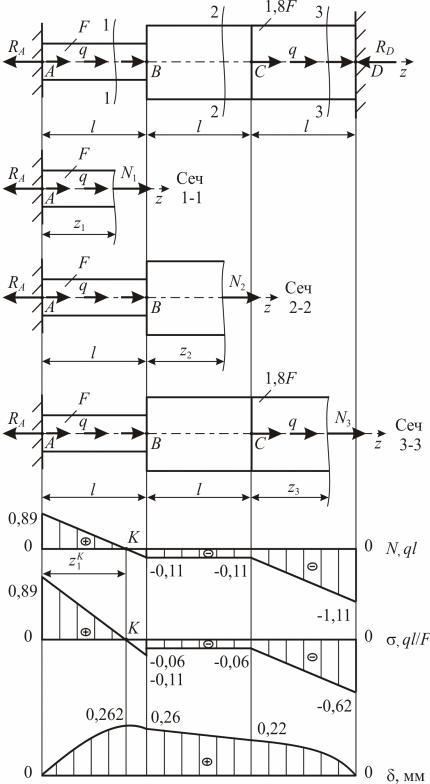
а

б

в

г

д

е

ж

Рис. 1.7

31

Юнга; Fi – площадь поперечного сечения; li – длина участка бруса. В случае

постоянной по участку продольной силы li Ni li .

EFi

Сначала запишем для каждого участка бруса продольные усилия и абсолютные деформации. Продольные силы определяем методом сечений, рассматривая отсечѐнные части каждого участка (рис. 1.7, б, в, г), начиная со свободного конца. При этом продольную силу изображаем положительной, т.е. растягивающей рассматриваемый участок.

Используя уравнение равновесия отсечѐнной части записываем последовательно продольные силы для каждого участка:

причѐм площади сечения возьмѐм по конфигурации бруса через неизвестное значение F:

Подставляя в (1.17) эти величины, получим уравнение перемещений, записанное через RA :

систему найдѐм величины этих реактивных сил. Уравнение (1.18) есть уравнение с одним неизвестным RA . Тогда, умножая его на EF, получаем

1,8 RA l 0,5ql 2 RA l ql 2 RA l 1,5ql 2 0 ,

32

3,8RA l 3,4ql 2 0 , RA 3,43,8ql 0,89ql .

Из уравнения (1.16) RD -RA 2ql 0,89ql 2ql 1,11ql . 2. Построим эпюру продольных сил N.

Подставив найденную реакцию RA в выражения продольных усилий по участкам, получим их значения:

N2 RA ql 0,89ql ql 0,11ql;

33

4. Условие прочности бруса

Условие прочности ступенчатого бруса при растяжении-сжатии по допускаемым нормальным напряжениям запишем по (1.5):

Выбираем max из полученных выше значений нормальных напряжений ζi как наибольшее по модулю,

Теперь условие прочности получаем в виде

0,89 ql

F

.

Найдѐм из этого условия требуемое значение F и назначим площади всех участков бруса, соблюдая указанное соотношение между ними.

F1 F 2,2 см2 , F2 F3 1,8F 1,8 2, 2 3,96 см2 .

5. Эпюры нормальных напряжений и продольных перемещений

Вычислим значения нормальных напряжений по участкам бруса, используя полученные выше выражения.

34

Откладывая полученные значения от базисной линии, построим эпюру распределения нормальных напряжений по длине балки (эпюру )

(рис. 1.7, е).

Построим эпюры продольных перемещений .

Сначала подставляем в полученные ранее выражения деформаций участков бруса найденные величины площадей и получаем значения деформаций.

0, 26 10 3 м=0,26 мм ;

Dопределяем с помощью (1.7):

δB l 1 0,26 мм; ;

δC l 1 l 2 0, 26 0,04=0,22 мм;

D l 1 l 2 l 3 0,26 0,04 0,22 0.

35

Продольное перемещение в сечении D оказался равным нулю, т.к. это сечение находится в заделке.

По полученным значениям построим эпюры продольных перемещений(рис. 1.7, ж). Уточним линию на первом участке, где имеем линейный характер силы N1 и пересечение еѐ эпюры с базисной линией в сечении K при z 1 z K1 :

Отложив это значение, проводим кривую с перегибом в точке K. Проверим условие жѐсткости, для этого из эпюры перемещений

возьмѐм δmax δK 0,262 мм и запишем δmax δK 0,262< δ =0,5 мм , значит, условие жѐсткости выполняется.

6. Касательные и нормальные напряжения в наклонной площадке

Для опасного сечения бруса вычислим касательные ηα и нормальные α напряжения в наклонной площадке, проведѐнной под углом α = 45° к оси бруса. Напряжения на наклонных площадках вычисляют по известным формулам (1.10):

ηα ζ2 sin 2α 1942 sin 2 45 =97 МПа ,

ζα ζ cos2 α 194 cos2 45 194 0,5=97 МПа .

7. Температурные напряжения

Вычислим температурные напряжения, возникающие при повышении температуры среды на 40°. Для этого составим уравнение перемещений (1.17), учитывая удлинение от температуры и сжатие от реакций, возникающих в заделках. При этом удлинение определяем по формуле

l t l Nt l .

EF

36

8. Влияние зазора на величину реакций

В случае зазора при действии температуры торец бруса переместиться за счѐт деформации на величину зазора. Поэтому величины реактивных сил должны удовлетворять уравнению перемещений, в котором правая часть равна 0,0001∙L1:

28 103 Н=28 кН.

Как видим, значение температурных реакций при наличии зазора уменьшается.

Задача 5. Проектный расчѐт стержневой статически неопределимой системы при растяжении и сжатии

37

В статически неопределимой стержневой системе абсолютно жѐсткий брус AB опирается на шарнирно-неподвижную опору и прикреплен двумя упругими стержнями к неподвижной опорной поверхности (рис. 1.8, а). Брус несѐт нагрузку известной величины, l 1,6 м , q = 20 кН/м; P 2 ql .

Требуется:

1.Найти усилия в упругих стержнях, используя уравнения равновесия и уравнение перемещений.

2.Подобрать площади поперечных сечений стержней, используя условия прочности по допускаемым напряжениям и по методу предельного со-

стояния, если допускаемое напряжение =200МПа, предел текучести т = 320МПа, запас прочности n = 1,6.

3. Вычислить температурные напряжения, возникающие в стержнях при повышении температуры среды на 15˚С. Принять коэффициент линейного удлинения =1,25∙10-5 1/град.

Решение 1.Нахождение усилий в стержнях.

Статически неопределимые стержневые системы – это системы, в которых количество стержней превышает количество уравнений равновесия.

Брус АВ имеет шарнирно подвижные опоры в точках А и В и шарнирнонеподвижную в точке K. В опорах возникают реакции RAC, RBD, RK и HK (рис. 1.7, б). Для плоской системы можно составить три уравнения равновесия, а неизвестных четыре, значит, заданная система имеет одну «лишнюю» связь (с точки зрения статики), и степень ее статической неопределимости 1 .

При расчѐтах необходимо знать продольные силы, возникающие во всех стержнях. Для нахождения этих усилий дополнительно к уравнениям равновесия составляют уравнения, учитывающие характер деформации системы. Их называют уравнениями перемещений (или уравнениями совместности деформаций). Число их равно количеству «лишних» связей системы и характеризует степень еѐ статической неопределимости. Использование уравнений перемещений основано на том, что деформации стержней можно выразить через неизвестные продольные силы по формуле

l Nl и сравнить между собой.

EF

Под действием внешней нагрузки брус АВ займет положение А1В1 (рис.

1.7, г). Горизонтальными перемещения концов А и В пренебрегаем в силу малости деформаций в несущих конструкциях. Отрезок АА1 есть деформация стержня АС, назовем еѐ l1 . На первоначальной длине стержня DВ отложим

38

усилие N2 − сжимающим. Или выполнив разрез системы по шарнирам А и В (рис. 1.8, в), покажем усилиями N1 и N2 воздействие разрезанных частей системы друг на друга. Здесь хорошо видно, что N1 и N2 вызывают

соответственно растяжение и сжатие стержней. Как известно, деформации связаны с продольными усилиями:

39

а

б

в

Рис. 1.8

40