
численные методы моделирования
.pdf
20
Gок ,tок , tок
Dп , Pп , tп , hп
Pд
Gпв ,tпв ,tпв
Рис. 3.4. Расчетная схема деаэрационной установки
Для определения неизвестных величин необходимо совместно решить уравнения материального и теплового балансов:
Dп + Gок = Gпв
Dпhпηт + Gокtок = Gпвtпв ,
где tпв = h′(Pд ) – энтальпия питательной воды (насыщенная среда) на выходе из деаэрационной установки; Pд – давление в деаэраторе.
Конденсатор. Предназначен для конденсации отработавшего в турбине пара за счет охлаждающей технической (циркуляционной) воды. При этом также полагают, что все процессы происходят на линии насыщения, а давле- ние в конденсаторе Pк является известной величиной. Параметры охлаж- дающей воды определяются так же, как для соответствующих потоков у по- догревателя поверхностного типа. При этом расход основного конденсата на выходе из конденсатора Gок равен расходу пара в конденсатор Dк (см. рис.
3.5). Задача расчета конденсационной установки сводится к определению эн- тальпии основного конденсата пара на выходе, которая в свою очередь вы-
числяется как энтальпия насыщенной жидкости в зависимости от давления пара в конденсационной установке: tок = h′(Pк ) .
Dк , hк
Gцв ,tцв
Pк
Gок ,tок , tок
Рис. 3.5. Расчетная схема конденсационной установки

21
Точки смешения и разветвления. Являются элементами тепловой схемы
и предназначены для смешения или разветвления различных материальных потоков (см. рис. 3.6).
|
|
|
|
|
|
|
||
Gсм ,tсм ,t |
см |
|
Gв ,tв ,t |
в |
||||
|
|
|
|
|
|
|
|
|
Gд , tд , tд
Рис. 3.6. Расчетная схема точки смешения
Целью расчета любой точки смешения является определение одного из расходов теплоносителя, подходящего к точке (Gв или Gд ), и температуры
теплоносителя, получающейся в результате смешения потоков (tсм ). Для
решения поставленной задачи, как и в случае расчета подогревателя смешивающего типа и деаэрационной установки, необходимо составить, систему уравнений, состоящую из уравнений материального и теплового балансов:
Gв + Gд = Gсм
Gвtв + Gдtд = Gсмtсм
Расширитель непрерывной продувки. Данные устройства используются в тепловой схеме ТЭС для утилизации тепла потока продувочной воды, по- ступающей из соленых отсеков барабанов паровых котлов. Принцип работы
расширителей непрерывной продувки основан на резком изменении давления продувочной воды ( Gпр ) от давления в барабане или выносном циклоне котла
( Pб ) до давления в расширителе ( Pр ). За счет резкого перепада давлений про-
исходит вскипание продувочной воды, сопровождаемое образованием обес- соленного насыщенного пара, который далее используется на технологиче- ские нужды и продувочную воду с повышенной концентрацией растворен- ных в ней солей. Если расширители в тепловой схеме используются односту- пенчатые, то давление в расширителе ( Pр ) обычно поддерживается равным
0,7 МПа. Если схема включения расширителей двухступенчатая, то в аппара- те первой ступени давление равно 0,7 МПа, а второй ступени – 0,12 МПа.
Целью расчета расширителя непрерывной продувки является опреде- ление расхода вторичного пара Dп′ и расхода соленой продувочной воды по-
сле расширителя Gпр′ (см. рис. 3.7).
Для определения искомых величин необходимо составить систему ли-
нейных алгебраических уравнений из уравнений материального и теплового балансов:

22
Dп′ , hп′
Gпр ,tпр ,tпр
Pр
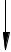 Gпр′ ,t′пр ,tпр′
Gпр′ ,t′пр ,tпр′
Рис. 3.7. Расчетная схема расширителя непрерывной продувки
Gпр = Dп′ + Gпр′
G |
|
|
|
= D′h′ |
+ G′ t |
′ |
, |
t |
пр |
||||||
|
пр |
п п |
пр пр |
||||
где hп′ = h′′(Pр ) – энтальпия насыщенного пара, определяемая по давле- нию в расширителе; tпр′ = h′(Pр ) – энтальпия насыщенной соленой воды на вы- ходе из расширителя; tпр = h′(Pб ) – энтальпия продувочной воды на входе в
расширитель.
Испарительная установка. Используется в тепловых схемах ТЭС для генерации вторичного, влажного насыщенного пара из добавочной воды за счет тепла пара, отбираемого из проточной части турбины или коллектора собственных нужд (см. рис. 3.8).
Dп , Pп , tп , hп
Dп′ , hп′
Dп , tд , tд
Gдв , Pдв ,tдв ,tдв
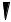 Gпр ,tпр ,tпр
Gпр ,tпр ,tпр
Рис. 3.8. Расчетная схема испарительной установки
Целью расчета испарителя является определение расхода греющего па- ра Dп , расхода вторичного пара Dп′ или расхода продувочной воды Gпр на

23
выходе из установки. Для определения искомых величин необходимо соста- вить уравнение теплового баланса испарителя, дополненное уравнением ма- териального баланса по добавочной воде:
Dпhпηт + Gдвtдв = Dпtд + Dп′hп′ + Gпрtпр Gдв = Dп′ + Gпр ,
где tд = h′(Pп ) – энтальпия дренажа греющего пара; hп′ = h′′(Pдв ) – энталь- пия получаемого насыщенного вторичного пара; tпр = h′(Pдв ) – энтальпия про-
дувочной воды на выходе из испарителя.
Насос. Имеет однозначную расходную характеристику, поэтому задача
его расчета сводится к оценке величины прироста энтальпии в результате сжатия теплоносителя с давления на входе Pвс до давления нагнетания Pн .
|
|
в′ |
|
|
|
|||
Gв , Pн ,t |
Gв , Pвс , t |
в |
||||||
|
|
|
|
|
|
|
|
|
Рис. 3.9. Расчетная схема насосной установки
Тогда математическая модель насоса может быть записана в следую- щем виде:
tв′ = tв + t
|
|
|
(Pн − Pвс )vвс |
|
2 , |
|
t = |
10 |
|||||
ηн |
|
|||||
|
|
|
|
|
||
где vвс – удельный объем теплоносителя на входе в насос; ηн – к.п.д. на-
соса (принимается в расчетах равным 0,6÷0,8).
Водо-водянной теплообменник. Целью расчета теплообменников, в ко- торых греющим теплоносителем является вода (дренаж греющего пара, про- дувочная вода и др.), является энтальпия и соответственно температура на- греваемой среды на выходе из аппарата. Принцип расчета такой установки совпадает с принципом расчета охладителя дренажа (ОД) подогревателя по- верхностного типа.
Определение расходов греющего пара на регенеративный подогрев в получаемых системах линейных алгебраических уравнений производится с использованием численных методов решения подобных систем. Для этого уравнения балансов приводят к следующему виду [3]:
ìa11 x1 + a12 x2 + a13 x3 + ... + a1n xn = b1 |
|
|
|||||||||||||
ïa |
x + a |
22 |
x |
2 |
+ a |
23 |
x |
3 |
+ ... + a |
2n |
x |
n |
= b |
2 |
|
ï |
21 1 |
|
|
|
|
|
|
|
|||||||
ï |
|
|
|
|
+ a33 x3 |
+ + a3n xn |
= b3 |
|
|||||||
ía31 x1 + a32 x2 |
|
||||||||||||||
ï..................................................... |
|
|
|
||||||||||||
ï |
x + a |
|
x |
|
+ a |
|
x |
|
+ + a |
|
x |
|
= b |
|
|
ïa |
n2 |
2 |
n3 |
3 |
nn |
n |
n |
, |
|||||||
î |
n1 1 |
|
|
|
|
|
|
||||||||
24
где aij – значения коэффициентов при неизвестных; xi – искомые кор- ни системы (неизвестная величина); bi – значения правых частей уравне-
ния.
Так, применительно к расчету теплообменника поверхностного типа состоящего из охладителя пара, собственно подогревателя и охладителя дре- нажа (см. рис. 3.2) такая система будет выглядеть следующим образом:
ìDп ( ïí Dп ïî Dп
hп - hп¢ )ηт - Gв tоп
(hп¢ - tд )ηт + Gв tод
(tд - tд¢)ηт - Gв tод
=-Gв tсп
=Gв tсп
= -Gв tв ,
где
a11 = (hп − hп′ )ηт |
a12 = −Gв |
a13 = 0 |
|
|
|
|
|
|
|
||||||
b1 = −Gв t |
сп |
||||||||||||||
a21 = (hп′ − t |
|
д )ηт |
a22 |
= 0 |
a23 = Gв |
|
|
|
сп |
||||||
|
b2 = Gв t |
||||||||||||||
|
|
|
|
д′)ηт |
a32 |
= 0 |
a33 = −Gв |
|
|
|
|
|
|
в |
|
a31 = (t |
д − t |
b3 = −Gв t |
|||||||||||||
Для решения |
систем линейных |
алгебраических уравнений (СЛАУ) |
|||||||||||||
применяют в основном два класса методов: прямые и итерационные [4]. Прямые методы являются универсальными и применяются для решения сис- тем сравнительно невысокого порядка ( n < 200 ). К числу таких методов отно- сятся метод Крамера, метод Гаусса и т.д.
Итерационные методы эффективно использовать для решения СЛАУ высокого порядка со слабо заполненными матрицами. Яркими представите- лями подобного класса методов являются методы Якоби и Зейделя.
Метод Крамера для решения систем алгебраических уравнений осно- ван на их матричном представлении: Ax = B ,
|
a11 |
a12 |
a13 |
...a1n |
|
|
|
|
x1 |
|
|
b1 |
|
|
где A = |
a21 |
a22 |
a23 |
...a2n |
, |
|
x = |
|
x2 |
, |
B = |
b2 |
. |
|
|
... ... ... |
... |
|
|
|
|
|
... |
|
|
... |
|
||
|
an1 |
an2 |
an3 ...ann |
|
|
|
|
xn |
|
|
bn |
|
||
Согласно методу, определение матрицы неизвестных величин x осу- |
||||||||||||||
ществляется по формуле: |
xi = |
i |
, |
где |
|
– |
значение главного определителя, |
|||||||
|
|
|||||||||||||
составленного из |
коэффициентов |
при |
неизвестных aij − A; i – значение |
|||||||||||
вспомогательных определителей, образованных из главного путем замеще- ния соответствующего i - го столбца матрицы A на столбец значений правой
части системы – |
B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Количество вспомогательных определителей в данном случае будет |
|||||||||||||||||||
равно числу искомых переменных – |
n . Например, |
|
|
|
|
|
|
|
|||||||||||
|
b1 |
a12 |
a13 |
...a1n |
|
|
a11 |
b1 |
a13 |
...a1n |
|
|
|
a11 |
a12 |
a13 |
...b1 |
|
|
|
|
|
|
|
|
||||||||||||||
1 = |
b2 |
a22 |
a23 |
...a2n |
, |
2 = |
a21 |
b2 |
a23 |
...a2n |
|
, |
n = |
a21 |
a22 |
a23 |
...b2 |
|
. |
|
... ... ... ... |
|
|
... ... ... ... |
|
|
|
... ... ... ... |
|
|
|||||||||
|
bn |
an2 |
an3 |
ann |
|
|
an1 |
bn |
an3 |
ann |
|
|
|
an1 |
an2 |
an3 |
bn |
|
|

25
Метод Гаусса является одним из самых распространенных методов решения систем линейных алгебраических уравнений. Этот метод называют также методом последовательного исключения неизвестных.
Вычисления с помощью метода Гаусса состоят из двух основных эта-
пов, называемых прямым ходом и обратным ходом.
Прямой ход метода Гаусса заключается в последовательном исключе- нии неизвестных из системы линейных алгебраических уравнений для пре- образования ее к эквивалентной системе с верхней треугольной матрицей. Вычисление значений неизвестных проводят на этапе обратного хода.
Рассмотрим схему решения СЛАУ методом Гаусса.
Прямой ход. На первом шаге алгоритма исключают неизвестное x1 из уравнений с номерами 2, 3, 4, …, n . Чтобы исключить x1 из i -го уравнения,
необходимо первое уравнение умножить на отношение ai1 и вычесть его из
a11
i -го уравнения. Это позволит обратить в нуль коэффициенты при x1 во всех уравнениях, кроме первого. В результате получим эквивалентную систему.
На втором шаге исключаем из полученной системы неизвестное x2 из уравнений 3, 4, …, n . Множители второго шага вычислим по выражению
ai(21) |
и вычислим последовательно из третьего, четвертого и …, n -го уравне- |
|
a22(1) |
||
|
ний ранее преобразованной СЛАУ второе уравнение, умноженное на соот- ветствующие множители.
Аналогично проводятся остальные шаги. После ( n −1) – го шага ис- ключения получают систему уравнений следующего вида:
ìa11 x1 |
+ a12 x2 |
+ |
a13 x3 |
+ |
... + a1n xn |
= b1 |
||||||
ï |
(1) |
+ |
a |
(1) |
x3 |
+ |
... + a |
(1) |
|
|
(1) |
|
ï |
a22 x2 |
23 |
2n xn |
= b2 |
||||||||
í |
|
|
a |
(2) x |
3 |
+ |
... + a |
(2) x |
n |
= b(2) |
||
ï |
|
|
33 |
|
|
|
3n |
|
3 |
|||
|
|
|
|
|
|
|
.................... |
|||||
ï |
|
|
|
|
|
|
|
(n−1) |
|
|
|
(n−1) |
ï |
|
|
|
|
|
|
|
xn |
|
|
||
î |
|
|
|
|
|
|
|
ann |
= bn |
|||
|
Полученная матрица A(n−1) |
|
является верхней треугольной матрицей. На |
|||||||||
этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения треугольной системы находят xn . Подставляя найденные значения xn в предпоследнее уравнение, получают
xn−1 . Осуществляя обратную подстановку, далее последовательно находят не-
известные xn−2 , xn−3 ,..., x3 , x2 , x1 .
Нетрудно заметить, что для реализации метода Гаусса требуется (2/3) n2 арифметических действий, причем подавляющее число действий со- вершается на этапе прямого хода [5].
26
Задание к работе и порядок ее выполнения
1. В соответствии с вариантом задания, составить систему уравнений, описывающих узел тепловой схемы.
2.Разработать блок-схему алгоритма расчета узла тепловой схемы, ко- торая включает ввод исходных данных, определение параметров воды, дре- нажа и пара, определение искомых величин и вывод на печать полученных результатов.
3.Составить программу расчета теплообменника с наглядной печатью исходных данных, результатов расчета.
Исходные данные к лабораторной работе №3
Вариант №1
Определить расход греющего пара на теплообменник поверхностного типа, составленный из двух частей: собственно подогревателя (СП) и встро- енного охладителя дренажа (ОД). Греющий пар подводится к СП, где проис- ходит его конденсация, и затем поступает в ОД, в котором происходит пере- охлаждение конденсата пара. В СП также сливается дренаж Dд с предвклю-
ченного теплообменника. Переохлажденный конденсат с ОД сливается кас- кадно в точку смешения (СМ). Основной конденсат после точки смешения затем последовательно подогревается в ОД и СП.
Dп , Pп , tп
ПНД
′ |
G |
см |
, t |
см |
Gок , Pок , tок |
|
tсм |
tод |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОД |
|
|
|
|
|
|
|
|
СМ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
СП |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t′′ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
D |
|
, t |
|
|
|
|
|
|
t′ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
д |
|
|
д |
|
|
|
д |
|
|
|
|
|
|
|
|
|
д |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дано:
Gок = 50 кг/с;
Pок = 1 МПа; tок = 40 °С; Dд = 5 кг/с; tд = 120 °С;
Pп = 0,15 МПа;
tп = 270 °С.
Определить:
Dп , Gсм , tсм , tод .
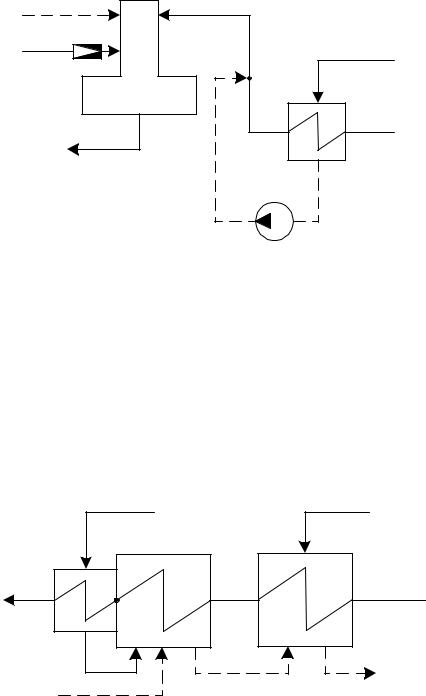
Вариант №2
Определить расходы греющего пара на деаэрационную установку и теплообменник поверхностного типа, представляющий собой подогреватель низкого давления (ПНД). Основной конденсат последовательно нагревается сначала в ПНД, смешивается в тоске смешения (СМ) с конденсатом греюще- го пара из ПНД и поступает в деаэратор. В деаэратор помимо греющего пара сливается дренаж Dд с предвключенного теплообменника. После деаэратора
питательная вода с расходом Gпв подается на всас питательных насосов.
27
Dд , tд |
|
Gсм , tсм |
|
|
|
|
|
|
Dп , Pп , tп |
Д |
D′ |
, P′ , t′ |
|
|
|
||
|
|
п |
п |
п |
|
|
|
|
|
|
СМ |
|
|
|
|
|
|
|
Pд |
|
|
|
|
|
|
|
|
|
t′ |
G |
ок |
, |
P |
, t |
ок |
|
Gпв , tпв |
ок |
|
|
ок |
|
||
|
СП |
|
|
|
|
|
|
|
|
|
ПНД |
|
|
|
|||
|
|
|
|
|
|
|||
tд
tд′
ДН
Дано:
Dд = 6 кг/с; tд =
180 |
°С; Pп = 0,7 |
|
МПа; tп = 170 °С; |
||
Pд = |
0,6 |
МПа; |
Gпв = 85 кг/с; Pп′= |
||
|
′ |
= 140 |
0,2 МПа; tп |
||
°С; Pок =1,1 МПа; |
||
tок = 35 °С. |
|
|
Определить: Dп , |
||
|
′ |
, Gок . |
Gсм , tсм , Dп |
||
Вариант №3
Определить расходы греющего пара на теплообменники поверхностно- го типа ПВД-1 и ПВД-2. ПВД-1 состоит из двух частей: охладителя пара (ОП) в котором пар охлаждается до параметров насыщения и собственно по- догревателя (СП) в котором происходит конденсация греющего пара. ПВД-2 состоит только из зоны СП. Конденсат пара с теплообменников сливается каскадно. В СП ПВД-1 сливается дополнительный дренаж пара с расходом Dд . Питательная вода последовательно нагревается сначала в ПВД-2, а затем
в ПВД-1.
|
|
Dп1, Pп1, tп1 |
|
Dп2 , Pп2 , tп2 |
|
|
Дано: |
|
|
|
|||
|
|
|
|
|
ПВД-2 |
|
|
|
Pп1 = 2 МПа; tп1 = |
||||
|
|
|
ПВД-1 |
|
|
|
|
300 °С; |
Pп2 =1,3 |
||||
t |
|
t |
|
t′ |
G |
|
, P |
, t |
|
МПа; tп2 = 270 °С; |
|||
оп |
сп |
пв |
пв |
Dд = 5 |
|
кг/с; |
tд = |
||||||
|
|
пв |
|
пв |
|
|
|||||||
|
|
ОП |
СП |
|
СП |
|
|
|
|
225 °С; |
|
Gпв = 120 |
|
|
|
|
|
|
|
|
|
кг/с; |
Pпв = |
16 |
|||
|
|
|
′ |
tд1 |
tд2 |
|
|
|
|
||||
|
|
Dд , tд |
tп |
|
|
|
|
МПа; tпв = 165 °С. |
|||||
|
|
|
|
|
|
|
|
|
Определить: |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Dп1, Dп2 , tоп . |
|
||
Вариант №4
Определить расходы греющего пара на теплообменники поверхностно- го типа ПНД-1 и ПНД-2. ПНД-2 состоит из двух частей: собственно подогре- вателя (СП) в котором происходит конденсация греющего пара и охладителя дренажа (ОД), предназначенного для переохлаждения конденсата пара. ПНД-

28
1 состоит только из зоны СП. Конденсат пара с теплообменников сливается каскадно. Основной конденсат последовательно нагревается сначала в ПНД- 2, а затем в ПНД-1.
|
Dп1, Pп1, tп1 |
|
ПНД-1 |
t′′ |
t′ |
ок |
ок |
СП |
|
Dд , tд |
tд1 |
Dп2 , Pп2 , tп2 |
|
|
ПНД-2 |
|
|
tод |
Gок , Pок , tок |
|
СП |
ОД |
|
|
|
|
t |
д2 |
t′ |
|
д2 |
|
Дано:
Pп1 = 0,45 МПа; tп1 = 200 °С; Pп2 = 0,2 МПа; tп2 = 160 °С; Dд = 4 кг/с; tд = 150 °С; Gок = 110 кг/с; Pок = 1,2 МПа; tок = 70 °С.
Определить:
Dп1, Dп2 , tод .
Вариант №5
Определить расход греющего пара на испарительную установку (И) и
расход вторичного насыщенного пара на подогреватель поверхностного типа низкого давления (ПНД), состоящего из зон собственного подогрева (СП) и охлаждения дренажа пара (ОД). В СП происходит конденсация греющего па- ра, а в ОД – переохлаждение конденсата ниже параметров насыщения. Вто- ричный пар в испарителе образуется из добавочной воды с расходом Dдв и
давлением Pдв . Неиспарившаяся часть добавочной воды сливается с продув- кой расходом Dпр .
|
|
|
|
|
D п , Pп , tп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дано: |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pп = 0,2 МПа; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
D ′ |
, h ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
п |
= 180 °С; |
||||
tд |
|
|
|
|
|
п |
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Dдв , Pдв , tдв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dдв = 8 кг/с; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tдв = 60 °С; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
П Н Д |
|
|
|
|
|
|
|
|
|
Pдв = 0,3 МПа; |
|||||||||||
|
|
|
|
|
Dпр , tпр |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gок = 20 кг/с; |
|||||||||||||
|
|
|
|
|
|
|
|
|
t ′ |
|
|
|
t |
|
|
|
|
|
|
|
|
G |
о к |
, P |
, t |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ок |
|
|
|
|
о д |
|
|
|
|
|
|
|
|
|
о |
к |
|
о |
P |
= 1,5 МПа; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О Д |
|
|
|
|
|
|
|
|
|
|
ок |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
С П |
|
|
|
|
|
|
|
|
|
|
|
tок = 20 °С. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t′ |
|
|
|
|
t′′ |
|
|
|
|
|
|
Определить: |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
д |
|
|
|
|
|
|
|
|
′ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dп , Dп , Dпр , tод |
||
29
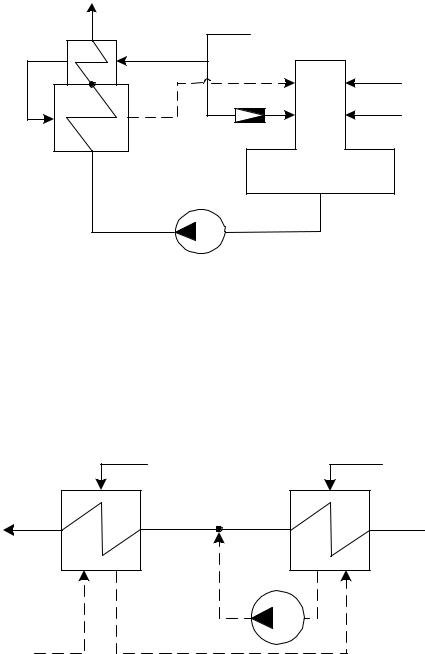
Вариант №6
Определить расходы греющего пара на деаэрационную установку и теплообменник поверхностного типа, представляющий собой подогреватель высокого давления (ПВД). ПВД включает в себя охладитель пара (ОП) и соб- ственно подогреватель (СП). В деаэратор помимо греющего пара поступает дренаж пара с ПВД, основной конденсат Gок и расход химически очищенной
воды Dхов . После деаэратора питательная вода с расходом Gпв подается на всас питательных насосов и далее на подогрев в ПВД.
|
t′′ |
ПВД |
|
пв |
|
|
ОП |
|
t′ |
|
tсп |
п |
СП |
|
|
|
|
Dп , Pп , tп |
|
|
|
G ок , Pок , tок |
tд |
РОУ |
D хов , tхов |
Д |
Pд
ПН
Дано:
Pп = 1,3 МПа; tп = 240 °С; Pд = 0,7 МПа; Gпв = 120 кг/с; Pок = 1 МПа; tок = 135 °С; Dхов = 10 кг/с; tхов = 30 °С.
|
t′ |
|
|
|
|
G |
пв |
, t |
пв |
|
|
|
|
|
|
Определить: |
||||
|
пв |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
, Gок . |
|
Вариант №7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dп , tпв |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определить расходы греющего пара на подогреватели низкого давле- |
||||||||||||||||||||
ния ПНД-1 и ПНД-2, представляющие собой собственно подогреватели (СП) |
||||||||||||||||||||
поверхностного типа. В ПНД-1 сливается дренаж пара Dд |
|
с другого тепло- |
||||||||||||||||||
обменника. Конденсат пара с ПНД-1 сливается в ПНД-2, а с ПНД-2 по пред- |
||||||||||||||||||||
включенной схеме с помощью дренажного насоса (ДН) в точку смешения |
||||||||||||||||||||
(СМ), располагающуюся между подогревателями. Основной конденсат по- |
||||||||||||||||||||
следовательно нагревается сначала в ПНД-2 затем в ПНД-1. |
|
|
|
|
|
|
||||||||||||||
|
Dп1, Pп1, tп1 |
|
|
|
|
|
|
Dп 2 , Pп 2 , tп2 |
|
Дано: Pп1 = 0,5 |
||||||||||
|
ПНД-1 |
|
|
|
|
|
|
|
ПНД-2 |
|
|
МПа; tп1 = 205 °С; |
||||||||
t′′ |
G |
|
, t |
|
СМ |
t′ |
|
|
|
G |
|
, P , t |
|
Pп2 = |
0,3 |
МПа; |
||||
см |
см |
|
|
|
ок |
ок |
t |
|
|
= 155 °С; |
D = |
|||||||||
ок |
|
|
|
ок |
|
|
|
|
ок |
п2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tд = |
д |
||
СП |
|
|
|
|
|
|
|
СП |
|
|
|
|
2 |
|
кг/с; |
160 |
||||
|
|
|
|
|
t′ |
ДН tд 2 |
|
|
|
|
°С;Gок = 95 кг/с; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Pок = |
1,2 |
МПа; |
|||||
|
|
|
|
|
д 2 |
|
|
|
|
|
|
|
|
|||||||
Dд , tд |
tд1 |
|
|
|
|
|
|
|
|
|
|
|
|
tок = 60 °С. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Определить: Dп1, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dп2 , Gсм , tсм . |
||||||
