
- •Министерство образования и науки Российской Федерации
- •Сибирский федеральный университет
- •Общая физика
- •Сборник контрольных заданий для студентов бакалавров
- •Введение
- •Часть 1
- •Кинематика
- •Динамика материальной точки и тела, движущегося поступательно
- •Механика твёрдого тела
- •Механические колебания
- •Молекулярная физика
- •Физические основы термодинамики
- •Электростатика. Постоянный ток.
- •Закон сохранения заряда:
- •Напряженность и потенциал электростатического поля:
- •Теорема Остроградского-Гаусса. Поток вектора напряженности через любую замкнутую поверхность, охватывающую зарядыq1, q2, …, qn, –
- •Объемная плотность энергии (энергия электрического поля, приходящаяся на единицу объема):
- •Согласно теореме косинусов, получим:
- •Решение. Воздух, являясь смесью идеальных газов, тоже представляет собой идеальный газ, и к нему можно применить уравние Менделеева–Клапейрона:
- •Решение. В основном уравнении молекулярно- кинетической теории –
- •Решение. Вычислим значения молярных теплоемкостей водорода, учитывая, что молекулы водорода – двухатомные, а число iстепеней свободы равно пяти:
- •Используя условие задачи и уравнение для изобарического процесса
- •Решение. Поскольку совершается адиабатический процесс, для решения используем уравнение адиабаты в виде
- •Решение. Термический кпд тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу:
- •Контрольные задания
- •Часть 2
- •Электромагнетизм.
- •Оптика. Атомная и ядерная физика
- •Контрольные задания
- •2. Некоторые внесистемные величины:
- •4. Молярные массы (м, 10-3 кг/моль) газов:
- •Библиографический список
- •Оглавление
- •Механика. Молекулярная физика. Электростатика. Постоянный ток. Электромагнетизм. Оптика. Атомная и ядерная физика. Контрольные задания для студентов бакалавров
- •660041, Г. Красноярск, пр. Свободный, 79
- •660041, Г. Красноярск, пр. Свободный, 82а
Согласно теореме косинусов, получим:
![]()
где
![]() – разность фаз составляющих колебаний.
– разность фаз составляющих колебаний.
Подставив
найденные значения φ2
и φ1,
получим, что
![]() (рад),
(рад),![]() Подставив значения А1,
А2,
и Δφ, найдем, что
Подставив значения А1,
А2,
и Δφ, найдем, что
![]() см.
см.
Пример
14.
Точка участвует одновременно в двух
гармонических колебаниях во взаимно
перпендикулярных направлениях. Колебания
описываются уравнениями x=
cos
πt
и y
= cos![]() t.
Определить траекторию движения точки.
t.
Определить траекторию движения точки.
Решение.
По условию задачи x=
cos
πt
; y
= cos![]() t.
(1)
t.
(1)
Для
определения траектории точки из выражений
(1) исключаем понятие времени. Искомые
уравнения имеют вид x=
2y2-1,
или
![]() ,
и представляют собой параболу.
,
и представляют собой параболу.
 Пример
15.
На
концах тонкого стержня длиной
Пример
15.
На
концах тонкого стержня длиной
![]() =1
м и массойm=400
г укреплены шарики малых размеров
массами m1=200
г и m2=300
г. Стержень колеблется вокруг горизонтальной
оси, перпендикулярной ему и проходящей
через его середину (точка О, см. рисунок).
Определить период Т колебаний, совершаемых
стержнем.
=1
м и массойm=400
г укреплены шарики малых размеров
массами m1=200
г и m2=300
г. Стержень колеблется вокруг горизонтальной
оси, перпендикулярной ему и проходящей
через его середину (точка О, см. рисунок).
Определить период Т колебаний, совершаемых
стержнем. 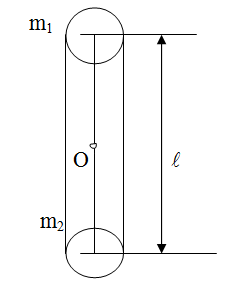
Решение. Период колебаний физического маятника, примером которого является стержень с шариками, определяется по формуле
![]() ,
(1)
,
(1)
где I – момент инерции маятника относительно оси колебаний; m – его масса; a – расстояние от центра масс маятника до оси.
Момент инерции данного маятника равен сумме моментов инерции шариков I1, I2 и стержня I3:
I= I1+ I2+ I3. (2)
Приняв шарики за материальные точки, выразим моменты их инерций:
![]() .
.
Момент
инерции стержня относительно оси,
проходящей через его середину, равен
I3=![]() .
Подставив полученные выраженияI1,
I2,
I3
в формулу (2), найдем момент инерции
физического маятника:
.
Подставив полученные выраженияI1,
I2,
I3
в формулу (2), найдем момент инерции
физического маятника:
![]()
=![]() .
.
Масса маятника состоит из масс шариков и стержня:
m = m1 + m2 + m3 = 0,2 + 0,3 + 0,4 = 0,9 кг.
Если ось x направить вдоль стержня и начало координат совместить с точкой О, см. рисунок, то искомое расстояние «а» равно координате центра масс маятника, т.е.
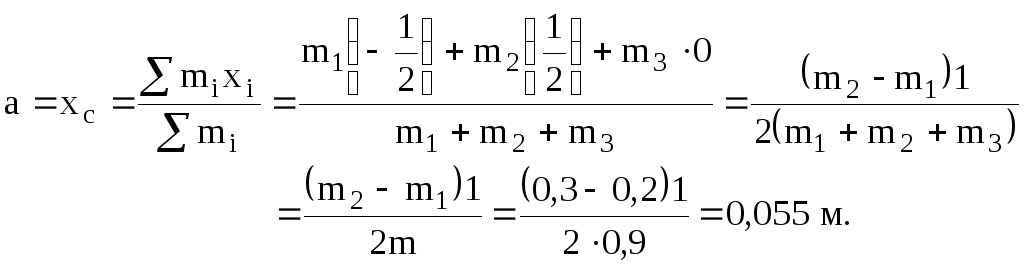
Произведя расчет по формуле (1), найдем период колебаний физического маятника:
![]() .
.
Пример 16. Найти молярную массу воздуха, считая, что он состоит из одной части кислорода и трех частей азота.
![]() =3210-3
кг/моль,
=3210-3
кг/моль,
![]() =2810-3
кг/моль.
=2810-3
кг/моль.
Решение. Воздух, являясь смесью идеальных газов, тоже представляет собой идеальный газ, и к нему можно применить уравние Менделеева–Клапейрона:
PV=![]() RT.
(1)
RT.
(1)
Для каждого компонента смеси (кислорода и азота) имеем:
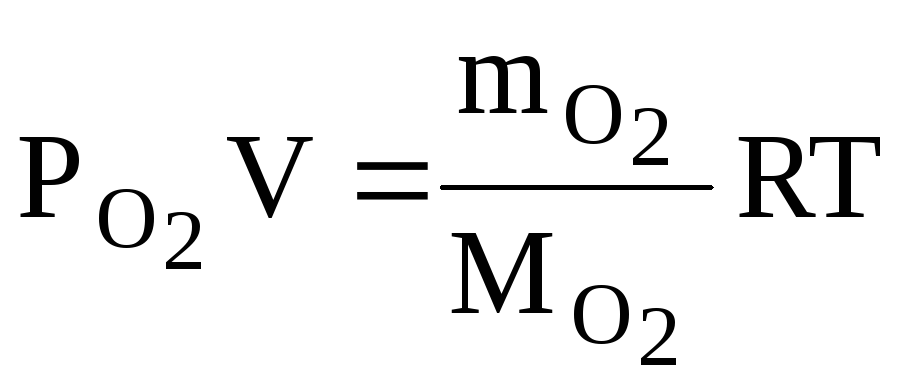 ,
(2)
,
(2)
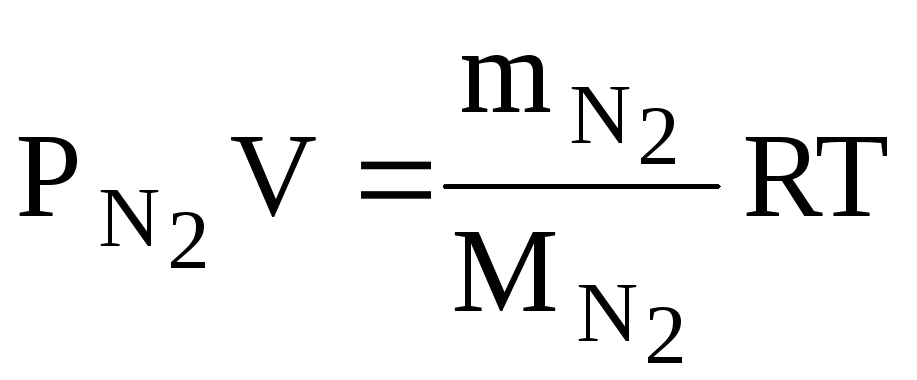 ,
(3)
,
(3)
где
![]() и
и
![]() – парциальные давления каждого
компонента.
– парциальные давления каждого
компонента.
По закону Дальтона
Рвозд
=
![]() +
+![]() .
.
Сложив (2) и (3), получим
(![]() +
+![]() )V
=
)V
=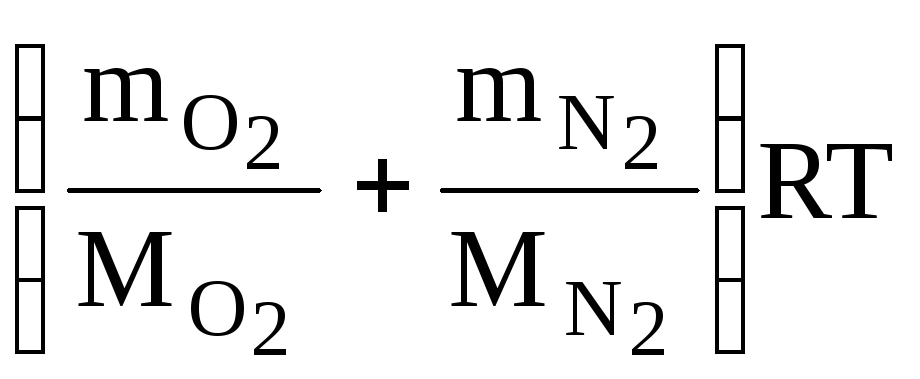 .
(4)
.
(4)
или на основании закона Дальтон
PV=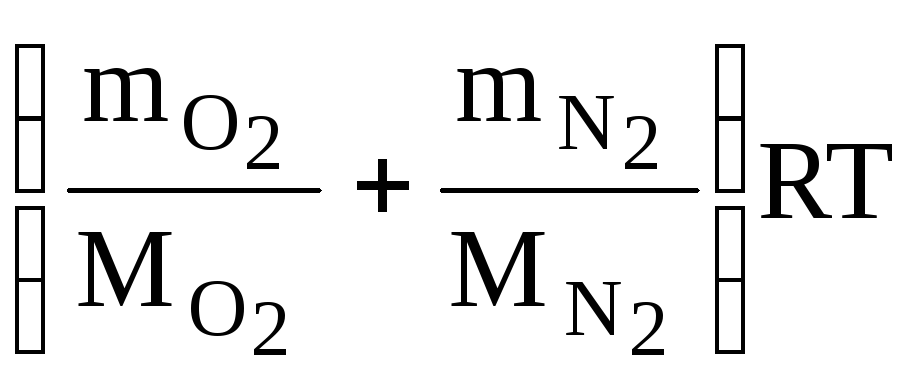 .
(5)
.
(5)
Сравнив
(1) и (5) с учетом того, что mвозд
=m![]() +m
+m![]() ,
имеем:
,
имеем:
Откуда
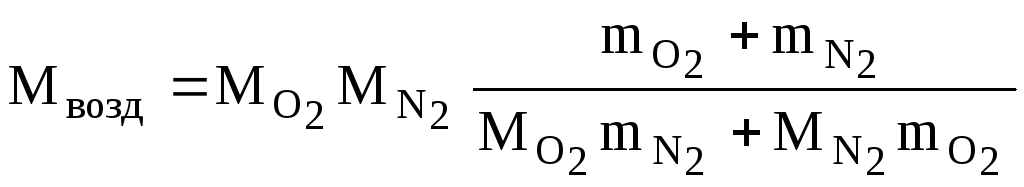 .
(6)
.
(6)
Подставив
в (6) равенство m![]() =3m
=3m![]() (по
условию), найдем молярную массу воздуха:
(по
условию), найдем молярную массу воздуха:
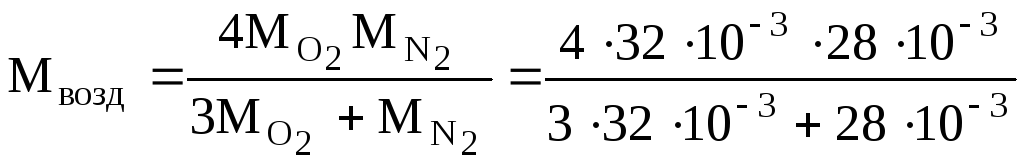 =2910-3
кг/моль.
=2910-3
кг/моль.
Пример 17. Плотность некоторого газа равна 6·10-2 кг/м3, а среднеквадратичная скорость молекул – 500 м/с. Найти давление, которое газ оказывает на стенку сосуда.
