
- •Работа l проверка выполнимости закона фарадея
- •Работа 2 определение чисел переноса в ионных проводниках
- •Работа 3 термодинамика гальванического элемента без переноса
- •Часть 1.
- •Часть 2.
- •Работа 4 установление константы диссоциации слабой кислоты методом эдс
- •Работа 5 определение константы диссоциации слабого электролита
- •Работа 6 определение растворимости малорастворимого соединения
- •Работа 7 определение стандартного окислительно- востановительного потенциала
- •Работа 8 потенциометрическое титрование
- •Работа 9 определение средней активности и среднего коэффициента активности соляной кислоты методом эдс
- •Работа 10 определение емкости двойного электрического слоя
- •Работа 11 перенапряжение разряда ионов водорода
- •Работа 12 перенапряжение диффузии при катодном восстановлении пероксида водорода
- •Работа13 полярографическое исследование кинетики электродного процесса
- •Работа 14 изучение кинетики электрохимических реакций хронопотенциометрическим методом
- •0Содержание
Работа 3 термодинамика гальванического элемента без переноса
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Для изучения термодинамики химических реакций целесообразно использовать гальванический элемент без переноса, в котором реализуются обратимые электродные реакции, а измерение ЭДС электрохимической цепи осуществляют в условиях равновесия, т.е. в отсутствии поляризации электродов.
Определяя экспериментально ЭДС гальванического элемента и ее температурную зависимость, и используя термодинамические соотношения, можно рассчитать изменения свободной энергии Гиббса, энтропии и энтальпии для химической реакции, протекающей в гальваническом элементе, а также – среднюю активность и средний коэффициент активности электролита.
Гальванический элемент без переноса можно представить схемой
К | КА| А, (1)
где К и А – электроды, обратимые относительно катиона и аниона электролита КА, соответственно.
Если на электродах гальванического элемента установилось равновесие, то измерением ЭДС обратимого элемента можно определить изменение свободной энергии Гиббса (∆G) химической реакции, протекающей в элементе при постоянных температуре T и давлении p , по следующему уравнению
– ∆G = nFE , (2)
где n – количество электронов, участвующих в химической реакции;
F – постоянная Фарадея, Кл/(моль эквивалентов);
E – величина ЭДС, В.
Уравнение (2) показывает, что электрическая работа nFE, совершается гальваническим элементом за счет убыли свободной энергии Гиббса в результате протекания реакции.
В качестве конкретного примера рассмотрим электрохимическую цепь
Cu, Ag, AgCl| CuCl 2 | Cu, (3)
в которой электролитом является раствор хлорида меди. Хлорид меди при растворении диссоциирует на ионы по реакции
CuCl2
![]() Cu2+
+ 2Cl–
.
(4)
Cu2+
+ 2Cl–
.
(4)
Правый электрод гальванического элемента обратим по катионам меди, а левый электрод обратим по хлорид-ионам.
На правом положительном электроде протекает реакция
Cu2+
+
2e
![]() Cu.
(5)
Cu.
(5)
и
потенциал электрода
![]() описывается уравнением Нернста
описывается уравнением Нернста
![]() =
=
![]() +
+
![]() ,
(6)
,
(6)
где
![]() –
стандартное значение потенциала;
–
стандартное значение потенциала;
![]() – активность ионов меди в растворе
электролита.
– активность ионов меди в растворе
электролита.
На левом отрицательном электроде протекает реакция
Ag
+ Cl–
–
е
![]() AgСl.
(7)
AgСl.
(7)
и
потенциал электрода
![]() описывается уравнением Нернста
описывается уравнением Нернста
![]() =
=
![]() –
–
![]() ,
(8)
,
(8)
где
![]() –
стандартное значение потенциала, В;
–
стандартное значение потенциала, В;
![]() – активность ионов хлора в растворе
электролита.
– активность ионов хлора в растворе
электролита.
Суммарную реакцию, протекающую в элементе, можно представить уравнением
2Ag
+ 2Cl–
+
Cu2+
![]() Cu + 2AgСl.
(9)
Cu + 2AgСl.
(9)
или в молекулярной форме
2Ag
+ CuCl2
![]() Cu
+ 2AgСl.
(10)
Cu
+ 2AgСl.
(10)
Выражение для ЭДС изучаемого элемента запишем в виде
Е=![]() –
–![]() =
=![]() +
+
![]() –
–![]() +
+
![]() (11)
(11)
или
Е
= Ео
+
![]() ,
(12)
,
(12)
где
Ео
=
![]() –
–![]() – стандартное значение ЭДС.
– стандартное значение ЭДС.
Согласно уравнению (4) и условию электронейтральности :
![]() =
=
![]() . (13)
. (13)
Известно, что активность аs соединения (соли) как целого можно представить уравнением
аs
=
![]() =
=
![]() ,
(14)
,
(14)
где:
![]() – средняя активность электролита;
– средняя активность электролита;
m – моляльная концентрация соли;
![]() –средний
коэффициент активности;
–средний
коэффициент активности;
![]() –число
катионов и анионов соответственно,
которое образуется при растворении и
диссоциации соли;
–число
катионов и анионов соответственно,
которое образуется при растворении и
диссоциации соли;
![]() .
.
В случае хлорида меди ν+ = 1, ν– = 2.
С учетом вышеизложенного, уравнение (12) можно записать в виде
Е
= Ео
+
![]() +
+![]() ,
(15)
,
(15)
Стандартная величина ЭДС Ео гальванического элемента (3) определяет константу равновесия реакции (9) К и связана с изменением стандартной энергии Гиббса в результате реакции ΔGo уравнением
Ео
=
![]() = –
= –![]() .
(16)
.
(16)
Из химической термодинамики известно, что
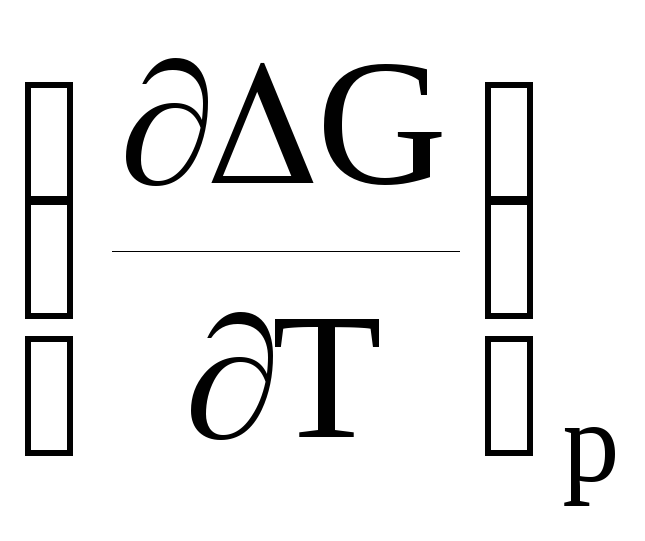 =
– ΔS
и ΔG
= ΔH
– TΔS
= ΔH
+ T
=
– ΔS
и ΔG
= ΔH
– TΔS
= ΔH
+ T![]() . (17)
. (17)
Тогда, согласно уравнениям (2) и (17)
–![]() =
ΔS
=
=
ΔS
=
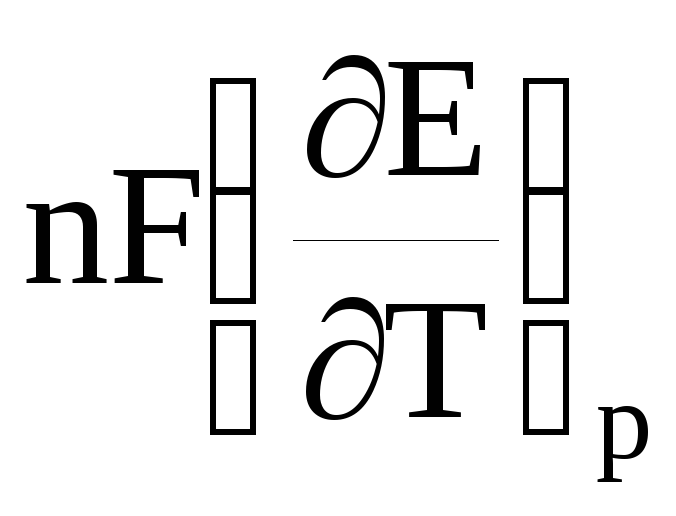 , (18)
, (18)
и
ΔH
= – nFE + nFT
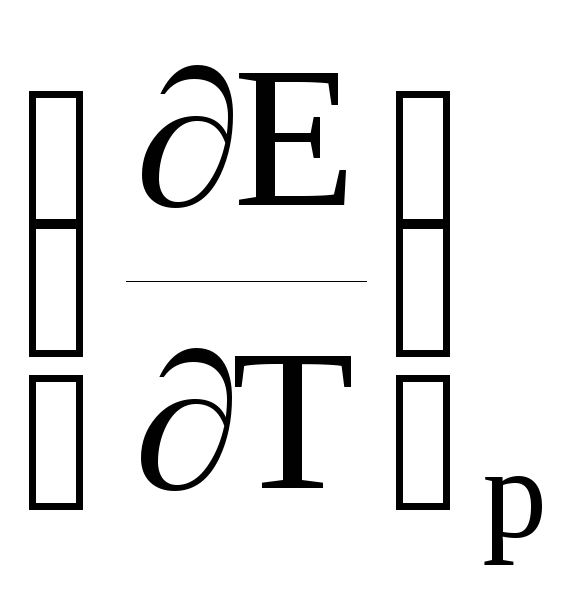 , (19)
, (19)
где
ΔH
и ΔS–
изменения энтальпии и энтропии,
соответственно, в результате реакции,
протекающей в гальваническом элементе;
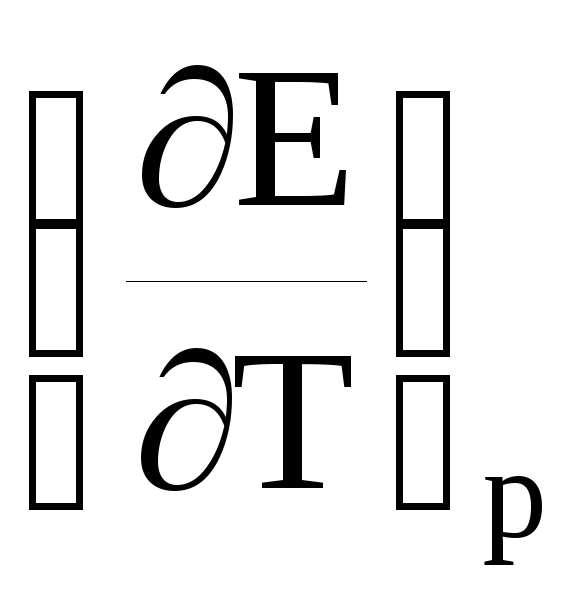 – температурный коэффициент ЭДС.
– температурный коэффициент ЭДС.
Температурный коэффициент ЭДС элемента может быть равен нулю, больше нуля или меньше нуля.
Когда
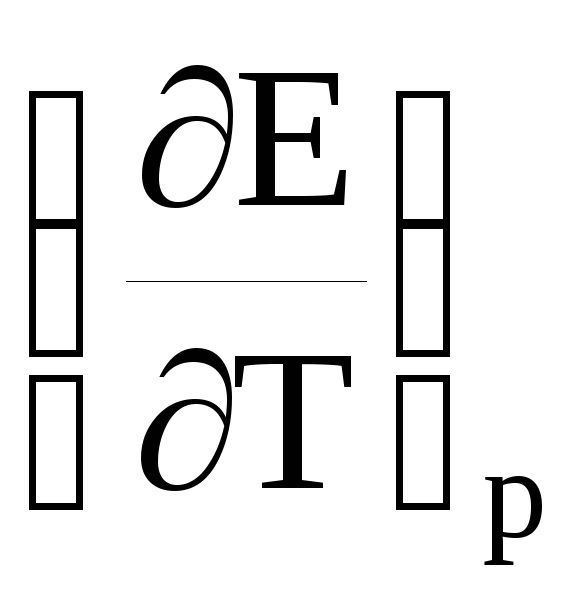 =
0 из уравнений (2) и (19) следует, что
=
0 из уравнений (2) и (19) следует, что
nFE = –ΔG = –ΔH. (20)
Если такой элемент будет работать в адиабатических условиях, то его температура не будет меняться.
В
случае, когда
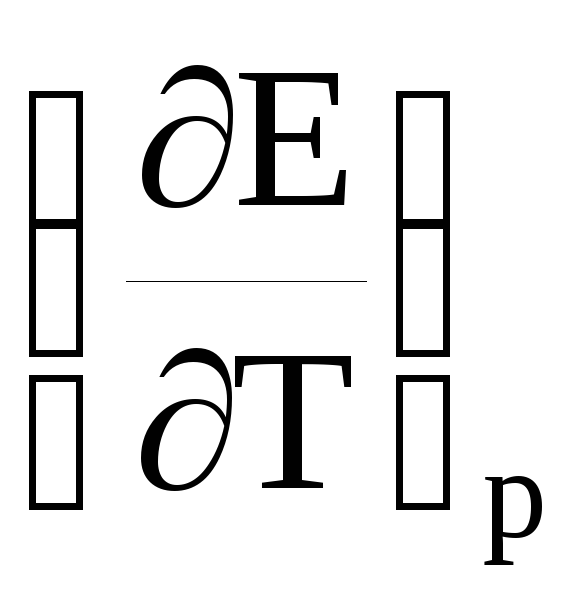 <
0,
<
0,
nFE = –ΔG < –ΔH (21)
и электрическая работа элемента меньше убыли энтальпии реакции. В адиабатических условиях температура в элементе будет повышаться.
Если
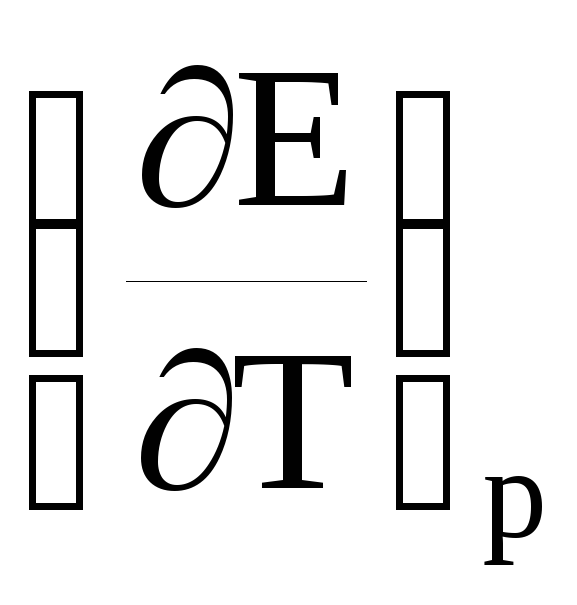 >0,
то
>0,
то
nFE = –ΔG > –ΔH, (22)
т.е. электрическая работа элемента больше изменения энтальпии при протекании реакции.
В этом случае в адиабатических условиях происходит понижение температуры гальванического элемента.
Таким образом, измерив ЭДС гальванического элемента при разных температурах, можно рассчитать ∆G, ∆S и ∆H реакции (9).
Используя
справочные данные по стандартным
значениям потенциалов медного
![]() и хлорсеребряного
и хлорсеребряного![]() электродов, которые при температуре
298К относительно водородного электрода
сравнения равны 0,337 В и 0,222 В соответственно
и уравнение (15), можно, рассчитать средний
коэффициент активности электролита
(CuCl2
).
электродов, которые при температуре
298К относительно водородного электрода
сравнения равны 0,337 В и 0,222 В соответственно
и уравнение (15), можно, рассчитать средний
коэффициент активности электролита
(CuCl2
).
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Целью работы является определение изменения термодинамических функций ΔG, ΔH, и ΔS в результате реакции, протекающей в гальваническом элементе (3), и среднего коэффициента активности γ± электролита.
Порядок выполнения работы
1. Из безводной соли готовят растворы хлорида меди с концентрацией m 0,001; 0,004; 0,007 и 0,01 моляльности по 50 мл каждого.
2. Готовят к работе медный электрод аналогично тому, как описано в работе 1.
3. Готовят хлорсеребряный электрод. Для этого серебряную проволоку поляризуют анодно в растворе (0,75 – 0,8)N HCl при плотности тока 0,6 мА/см2. Вторым электродом является платина. Процесс ведут до тех пор, пока серебряный электрод не приобретет коричневатый цвет. Следует избегать перехлорирования. Хлорированный электрод вымачивают в растворе (0,1– 0,2)N HCl. Обычно хлорсеребряный электрод готовится лаборантом заранее.
4. Собирают гальванический элемент (3), путем погружения в раствор хлорида меди, который предварительно заливают в электролизер, медного и хлорсеребряного электродов.
5.Подготовленный гальванический элемент помещают в термостат, в котором устанавливают температуру 298 К (m = 0,001).
6. После достижения указанной температуры элемент включают в измерительную цепь (см. рис.1 а,б).
Равновесную ЭДС определяют или компенсационным методом, подключая элемент к высокоомному потенциометру, или «прямым» измерением, подключая элемент к высокоомному цифровому вольтметру. Первый метод является более точным, поскольку во время измерения ток через гальванический элемент не течет, равновесие на электродах не нарушается и измеряется действительно равновесная ЭДС.
Компенсационным методом ЭДС измеряют в соответствии с инструкцией работы с потенциометром, «прямым» измерением ЭДС определяют в соответствии с инструкцией работы с высокоомным цифровым вольтметром. Инструкции предоставляет лаборант.
7. Измеряют ЭДС через каждые 10 минут, пока четыре последних измерения не покажут значения, совпадающие в пределах 1 мВ.
8. Повышают температуру до 308К и повторяют измерения ЭДС гальванической цепи указанным выше способом.

Рис. 1. Схема цепи для измерения равновесной ЭДС. а – компенсационным методом; б – прямым измерением. 1 – высокоомный потенциометр; 2 – источник постоянного тока; 3 – нормальный элемент; 4 – нуль-гальванометр; 5 – термостат; 6 – жидкость термостата; 7 – электролизер; 8 – раствор хлорида меди; 9 – медный электрод; 10 – хлорсеребряный электрод; 11 – термометр; 12 – высокоомный вольтметр
9. Для определения концентрационной зависимости среднего коэффициента активности электролита выполняют измерения ЭДС гальванического элемента при 298 К для растворов хлорида меди с концентрациями 0,004; 0,007 и 0,01 моляльности.
Измеренные величины заносят в таблицы 1 и 2.
Таблица 1. Температурные зависимости (m = 0,001).
-
Температура, К
ЭДС, В
Температурный коэффициент ЭДС, мВ/К
∆G, кДж
∆S, Дж/К
∆H, кДж
1
2
3
4
5
6
Таблица 2. Концентрационные зависимости (Т = 298К).
-
Концентрация CuCl2, моль/кг
ЭДС, В
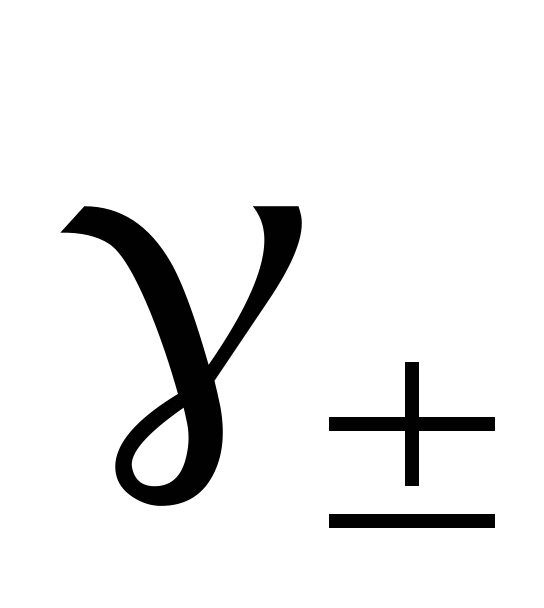
I
hэксп
hтеор
∆G, кДж
1
2
3
4
5
6
7
Обработка результатов эксперимента.
