Пример 2.6

В точке для заданного скалярного поля найти градиент и производную в направлении вектора , а также наибольшую скорость роста поля при переходе через точку М.

Решение. Скалярное поле задано функцией , значит, производная по направлению и градиент поля – это производная по направлению и градиент заданной функции.

Используем определение: градиент функции – это вектор с координатами . Найдем частные производные данной функции:

.

.

Вычислим значения этих производных в точке :

, .

Следовательно, градиент функции в точке М равен

.

Напомним, что градиент имеет простую физическую интерпретацию: этот вектор показывает направление, в котором при переходе через точку М скалярное поле растет быстрее всего.

Найдем производную функции в направлении заданного вектора, используя формулу:

,

где .

Вычислим направляющие косинусы вектора :

,

.

Тогда производная по направлению в произвольной точке имеет вид

.

В точке эта производная равна

.

С физической точки зрения, этот результат означает следующее: поскольку производная по направлению характеризует скорость изменения скалярного поля в заданном направлении, то в нашем случае скалярное поле при переходе через точку М убывает в направлении вектора .

Как уже отмечалось, скалярное поле при переходе через точку М возрастает быстрее всего в направлении градиента этого поля, при этом наибольшая скорость роста поля равна модулю градиента. Поэтому находим

,

таким образом, наибольшая скорость роста скалярного поля в точке М численно равна .

Пример 2.7

Даны точки и . Найти уравнение касательной плоскости и нормали к поверхности в той из этих точек, которая лежит на поверхности.

а) ;

б) .

Решение. а) Выясним, какая из точек А и В принадлежит поверхности, заданной уравнением , для этого подставим координаты точек в это уравнение

: , значит, точка А на поверхности не лежит;

: , следовательно, точка В принадлежит поверхности, поэтому уравнения касательной плоскости и нормали к поверхности будем искать в этой точке.

Используем уравнение касательной плоскости к поверхности в точке :

Чтобы записать это уравнение, найдем частные производные функции :

, .

Вычислим их значения в точке :

, .

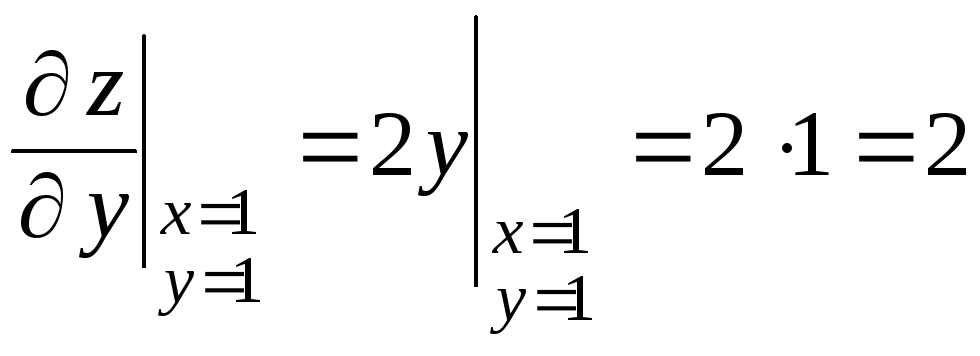Тогда уравнение касательной плоскости будет иметь вид

,

или .

Уравнения нормали к поверхности найдем по формуле

В нашем случае точка – это точка , значения производных функции мы уже вычисли, следовательно уравнения нормали к поверхности в точке В будут иметь вид

.

б) Определим какая из точек и принадлежит поверхности :

:   5 = 5 – верное равенство, значит, точка А лежит на данной поверхности;

:   , следовательно, точка В поверхности не принадлежит.

Найдем уравнения касательной плоскости и нормали к данной поверхности в точке А.

Для этого, так же как и в предыдущем примере, найдем производные от функции z по переменным х и у. Но в этом случае функция z задана уравнением , или , как неявная функция двух переменных, поэтому ее частные производные будем искать по соответствующим правилам:

,

.

Отсюда , .

Тогда уравнение касательной плоскости к поверхности в точке имеет вид

, или ,

а уравнения нормали –

, или .