
Задание 5.
Привести к каноническому виду уравнения кривых второго порядка. Построить кривые.
|
1.
а)
|
|
2.
а) |
|
3.
а) y
= 2x2
– 16x
+ 30; б) x2
+ 3y2
– 6x
– 12y
+ 12 = 0;
в) 3x2
– y2
– 18x
– 4y
+ 14 = 0; г) 4x2
– y2
– 24x
+ 4y
+32 = 0; д)
|
|
4.
а) y
= –x2
+ 6x
– 3; б) 4x2
– y2
+ 8x
– 4y
– 4 = 0;
в) x2
+ 3y2
– 6x
– 12y
+ 12 = 0; г) 3x2
+ 2y2
– 6x
+ 8y
+ 11 = 0; д)
|
|
5.
а) y
= 4x2
– 8x +
1; б) x2
+ 4y2
– 4x
– 8y
+ 4 = 0;
в) x2
– 9y2
– 4x
+ 18y
– 14 = 0; г) x2
– 2x
+ 4y2
– 16y
+ 21 = 0; д)
|
|
6.
а) y
= 0,5x2
– x
– 1; б) x2
+ 4y2
– 2x
– 16y
+ 13 = 0;
в) x2
– 4y2
– 4x
+ 8y
– 4 = 0; г) 3x2
+ y2
– 6x
+ 9 = 0; д)
|
|
|
|
|
Задание 6
Приведя к каноническому виду, определить, какую поверхность определяет уравнение. Построить поверхность.
-
4x2 – y2 + 4z2 – 8x + 4y + 8z + 4 = 0.
-
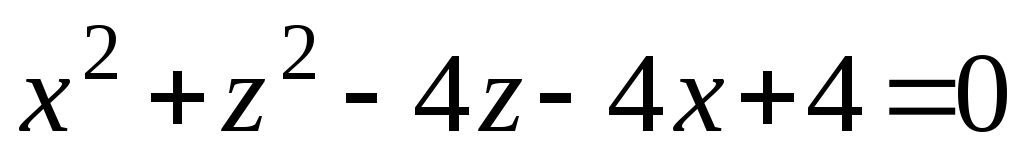 .
. -
4x2 – y2 + 4z2 – 8x + 4y + 8z + 4 = 0.
-
x2 + y2 – 6x + 6y – 4z + 18 = 0.
-
4x2 + 9y2 + 36z2 – 8x – 18y – 72z + 13 = 0.
-
x2 + y2 – z2 – 2y + 2z = 0.
-
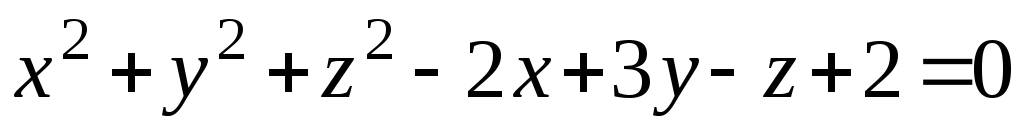
-
9x2 – z2 – 18x – 18y – 6z = 0.
-

-
 .
.
Задание 7
Методом сечений исследовать форму и построить поверхность:
1.
а) z2
= x
+ 3; б) y2
+
![]() z2
= 16 – 4x2.
z2
= 16 – 4x2.
2.
а)
![]() ;
б)
;
б)
![]() .
.
3. а) x – 9y2 = z2; б) x2 + y2 = 2x.
4. а) z = x2
+ 3; б) y2 +
![]() х2
= 16 – 4z2.
х2
= 16 – 4z2.
5.
а) y
– 9x2
= z2; б)
z
+ 2 =
![]()
6. а) y – 2
=![]() ; б).
; б).
![]()
7. а) z
– 2 =![]() ; б).
; б).
![]()
8. а) x2
= 4z2 +
![]() y2; б)
y2 = 25 +
y2; б)
y2 = 25 +
![]() z2.
z2.
9.
а)
![]() ; б)
; б)
![]() .
.
10.
а) z
= у2
+ 3; б) х2
+
![]() z2
= 16 – 4у2.
z2
= 16 – 4у2.
Задание 8
Определить, какие линии на плоскости определяют заданные уравнения. Уравнение, заданное в полярных координатах, преобразовать к уравнению в декартовых координатах. Построить эти линии.
1.
а)
![]() ; б)
; б)
![]() .
.
2.
а)
![]() ; б)
; б)
![]()
3. а)
![]() ; б)
; б)
![]()
4. а)
![]() ; б)
; б)
![]()
5. а)
![]() ; б)
; б)
![]()
6. а)
![]() ; б)
; б)
![]()
7. а)
![]() ; б)
; б)
![]()
8. а)
![]() ; б)
; б)
![]()
9. а)
![]() ; б)
; б)
![]()
10. а)
![]() ; б)
; б)
![]()
Задание 9
Заданы: уравнение линии, лежащей в координатной плоскости, и точка А . Требуется:
-
составить уравнение поверхности, образованной вращением этой линии вокруг указанной оси;
-
подобрать значение параметра р так, чтобы точка А лежала на этой поверхности;
-
сделать схематический чертеж поверхности.
-
-
5y2 + pz2 = 25 , A(1,2,1), ОУ
-
px2 = py + 1, A(-1,1,-2), ОУ
-
5px2 + z2 = 10p, A(-1,1,2), ОХ
-
pz2 = x, A(26,3,2), OХ
-
у2 = pz + 1, A(2,-5,1), ОZ
-
2px2 – y2 = 1, A(-1,1,2), ОХ
-
px2 = pz + 1, A(1,-2,-1), OZ
-
х2 = pу , A(-5,1,2), ОУ
-
у2 = z + p, A(-1,3,1), OZ
-
x2 = z2 + p, A(3,1,-1), ОZ
-
