Пример 1.2

Определить вид линий уровня функции . Построить линию уровня, проходящую через точку , а также линии уровня для . Построить график данной функции.

Решение. Область определения данной функции есть вся координатная плоскость. Линии уровня – это множество точек области определения, в которых функция принимает одно и то же значение. Уравнение линий уровня данной функции имеет вид , где С – произвольная постоянная; перепишем это уравнение в виде .

Для каждого конкретного значения С это уравнение определяет на плоскости ХОУ прямую. Следовательно, линиями уровня данной функции являются параллельные прямые с общим уравнением .

Выделим из них ту, которая проходит через точку . Для этого нужно найти такое значение С, при котором координаты точки М удовлетворяют уравнению линии уровня:

  .

Т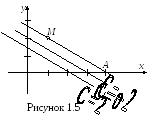 аким образом, через точку М проходит линия уровня с уравнением . На рисунке 1.5. это прямая АМ.

При получим линию уровня с уравнением , а при – с уравнением , они также изображены на рисунке 1.5.

П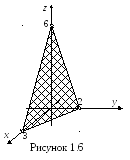 остроим график функции . В отличие от линий уровня, график функции двух переменных – это геометрическое место точек трехмерного пространства, координаты которых удовлетворяют заданному уравнению. Очевидно, данное уравнение , или определяет плоскость. Легко установить, что эта плоскость пересекает оси координат в точках , , . Таким образом, графиком данной функции является плоскость, часть которой изображена на рисунке 1.6.

Пример 1.3

Выразите длину хорды окружности как функцию радиуса и расстояния от хорды до центра окружности. Постройте три линии уровня этой функции.

Р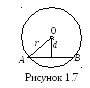 ешение. Пусть расстояние от хорды AB до центра О окружности равно d, радиус окружности равен r (рисунок 1.7). Обозначим длину хорды буквой L: . Тогда причем , .

Таким образом, длина L хорды AB есть функция переменных r и d, а закон, по которому каждой паре из области ставиться в соответствие единственное действительное число L, задается формулой . Множество D является областью определения этой функции, оно изображено на рисунке 1.8.

Н айдем линии уровня этой функции. Для этого в уравнении положим , где С – произвольная неотрицательная постоянная. Получим уравнения линий уровня

, или .

Построим линии уровня для , .

При уравнение линий уровня имеет вид , откуда , но в силу условия , получаем луч , .

П ри линия уровня имеет уравнение – это уравнение равнобочной гиперболы с центром в начале координат и полуосями , но также в силу условия , линия уровня данной функции есть только часть правой ветви этой гиперболы, расположенная в первой четверти.

Аналогично получим и при : линия уровня – это часть гиперболы

, или ,

расположенная в первой четверти. Эти линии уровня изображены на рисунке 1.9.

Пример 1.4

Определить вид поверхностей уровня функции . Построить одну из них.

Р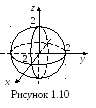 ешение. Область определения данной функции есть все множество точек трехмерного пространства. Семейство поверхностей уровня задается уравнением , , или

.

Это уравнение определяет семейство концентрических сфер с центром в начале координат и радиусами . На рисунке 1.10 изображена поверхность уровня данной функции для .

Пример 1.5

Найти пределы функций:

а) 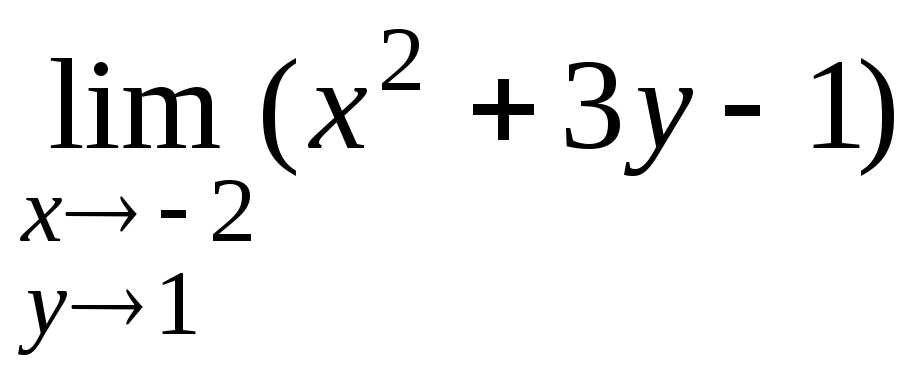; б)

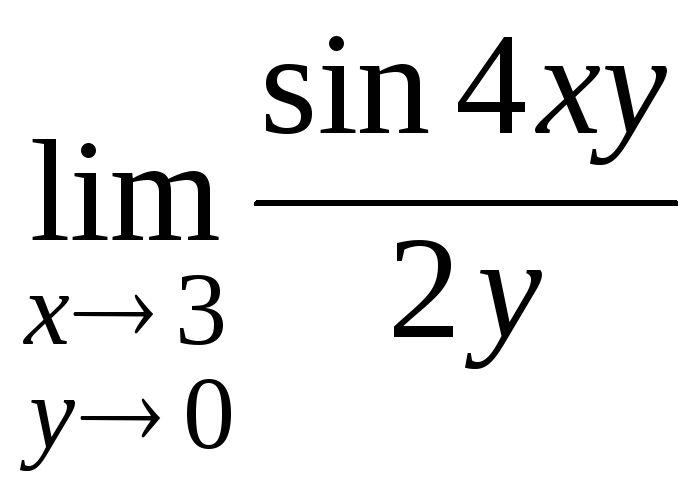в) г)

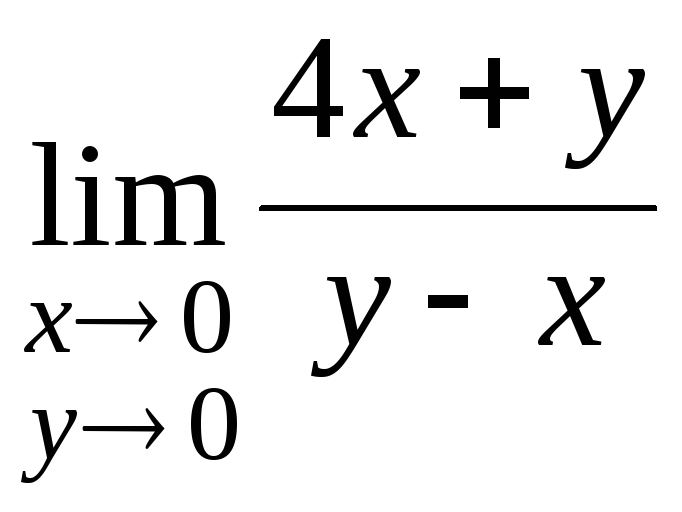
Решение.

а) Функция определена и непрерывна в точке , поэтому предел этой функции в точке равен значению функции в этой точке:

.

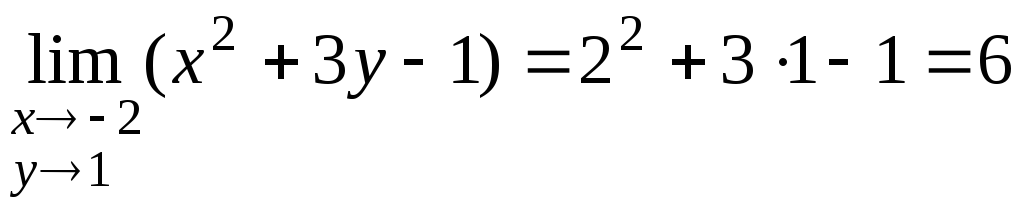б) Преобразуем функцию, предел которой требуется найти:

.

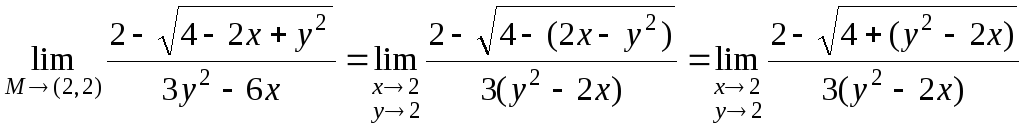Обозначим . Очевидно, при имеем . Тогда

.

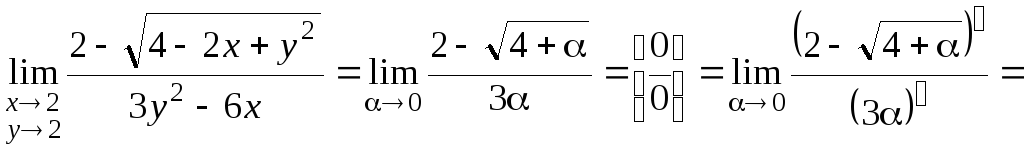
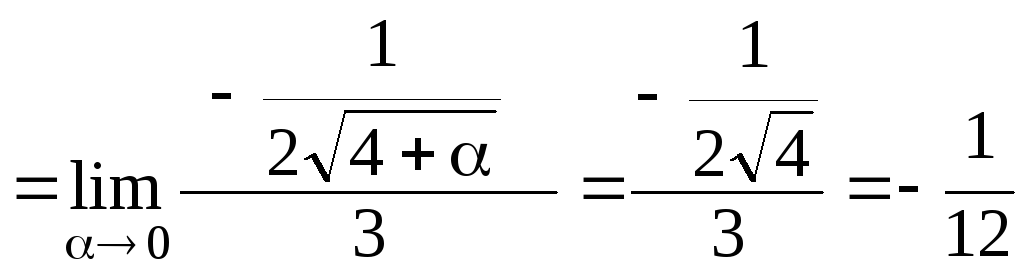Здесь мы воспользовались правилом Лопиталя.

в) Для вычисления 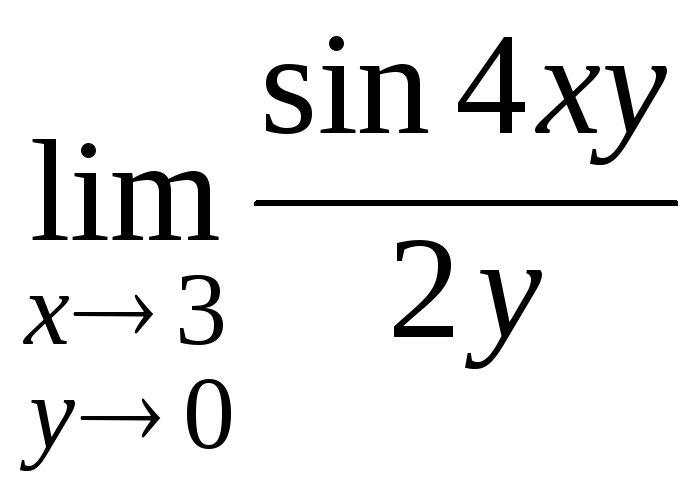выполним следующие преобразования:

.

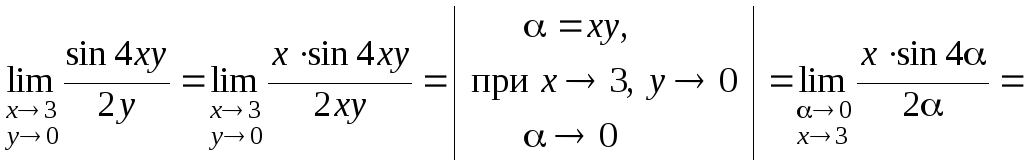
Здесь мы использовали первый замечательный предел.

г) Как следует из определения, , если , когда вдоль любой линии, соединяющей точки М и М₀. Рассмотрим 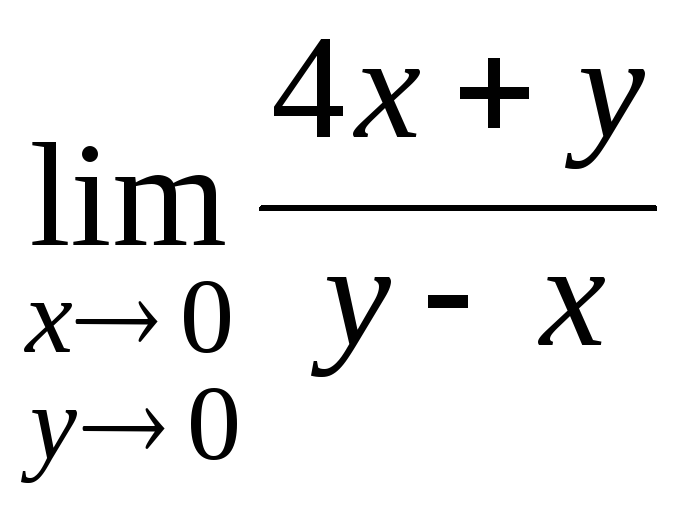, считая, что вдоль прямых . Получим

.

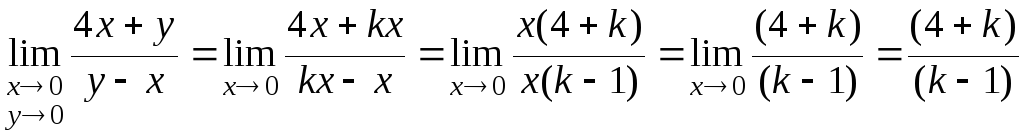Следовательно, значение предела функции зависит от углового коэффициента k прямой, по которой движется точка к точке . Это означает, что данная функция не имеет предела в точке .