1.7.2 Метод законов Кирхгофа

Рассмотрим расчет сложной цепи методом законов Кирхгофа.

Для схемы, приведенной на рисунке 1.31, дано: Е₁; Е₃; R₁; R₂; R₃.

Рисунок 1.31 - Расчетная схема

Найти

1. Все токи.

2. Проверить полученные результаты на баланс токов и баланс мощности.

3. Напряжения на всех элементах цепи.

4. Проверить напряжения на баланс напряжений.

Порядок расчета

1. Размечаем токи.

Как и ранее, токи размечаются стрелками непосредственно на проводах схемы. Стрелки токов направляются в произвольном направлении. Неизвестных токов будет столько, сколько имеется ветвей в сложной цепи. Индекс тока принимается равным индексу ветви.

2. Размечаем стрелки напряжений на элементах цепи. Стрелки расставляем не произвольно, а всегда против ранее размеченных стрелок токов. Произвольно стрелки напряжений размечать нельзя.

3. Составляем уравнения электрического состояния цепи.

Для решения нашей задачи требуется система из трех уравнений. По первому закону Кирхгофа число уравнений будет

. (1.56)

По второму закону Кирхгофа число уравнений будет

. (1.57)

Имеем:

; ;

; но , поэтому

; .

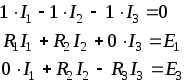. (1.58)

4. Решаем систему уравнений.

При решении уравнений можно использовать вычислительную технику или производить данную операцию вручную. В данном случае применим метод определителей (метод Крамера).

Имеем:

; ;

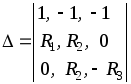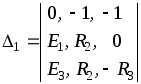(1.59)

; .

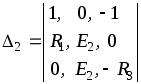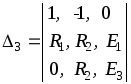Тогда токи будут равны:

; ;. (1.60)

5. Проверяем полученный результат на баланс токов.

Проверка производится во всех независимых узлах сложной цепи по первому закону Кирхгофа.

.

6. Проверяем полученный результат на баланс мощности.

По закону сохранения энергии количество выработанной в цепи и потребленной энергии должны быть равны.

Выработано

, если .

Израсходовано

.

При правильном значении токов имеем:.

Непосредственное применение законов Кирхгофа к расчету сложной цепи приводит к весьма громоздким вычислениям, так как приходится решать систему с большим числом уравнений. Поэтому, этот метод на практике применяется крайне редко из за его неэкономичности.

1.7.3 Метод контурных токов

Метод контурных токов был предложен известным английским физиком и электротехником Джеймсом К. Максвеллом. По этому методу цепь разбивается на ряд контуров, соприкасающихся друг с другом. Число контуров подсчитывается по формуле (1.14).

Предполагается, на время расчета, что каждый контур обтекается только присущим ему током, который называется контурным током.

Контурный ток - нереальный ток, он является вспомогательным средством при решении цепей.

Контурных токов столько, сколько имеется в цепи независимых контуров. Контуров в цепи всегда меньше числа ветвей, так как, даже для простого контура требуется, по крайней мере, две ветви.

Указанное обстоятельство приводит к тому, что контурных токов в цепи всегда меньше числа реальных токов.

Таким образом, основное преимущество метода контурных токов перед методом законов Кирхгофа состоит в сокращении числа расчетных уравнений.

По известным контурным токам, действительные токи определяются простым алгебраическим сложением.

Рассмотрим порядок расчета цепи указанным методом.

Для цепи, изображенной на рисунке 1.32, дано: Е₁; Е₃; R₁; R₂; R₃.

Рисунок 1.32 - Расчетная схема

Найти

1. Все токи.

2. Проверить полученные результаты на баланс токов и баланс мощности.

3. Напряжения на всех элементах цепи.

4. Проверить напряжения на баланс напряжений.

Порядок расчета

1. Размечаем контурные токи.

Направление токов выбирается произвольно, однако, где это возможно, желательно в смежных ветвях иметь их сумму.

2. Размечаем стрелки напряжений.

Стрелки напряжений расставляют по общему правилу, то есть всегда против ранее размеченных контурных токов. Стрелки напряжений снабжаются двумя индексами. Первый индекс - номер элемента, второй - номер контурного тока.

3. Составляем уравнения электрического состояния цепи.

Для этого обходим каждый контур в произвольном направлении и составляем уравнения по второму закону Кирхгофа

. (1.61)

4. Решаем уравнения электрического состояния цепи.

Решение, как и ранее, проводим с помощью определителей:

;

; (1.62)

.

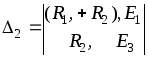Отсюда:

;

. (1.63)

5. Размечаем действительные токи в цепи.

Действительные токи можно направлять произвольно, однако, лучше учитывать при разметке направления и значения контурных токов, через которые они определяются. Стрелки действительных токов показаны на рисунке 1.32.

6. Определяем действительные токи.

Для этого имеем:

(1.64)

7. Проверяем значения токов на баланс токов.

Проверку производим в каждом узле цепи по первому закону Кирхгофа

. (1.65)

8. Проверяем значения токов на баланс мощности

. (1.66)

Метод контурных токов получил широкое распространение в инженерной практике, благодаря экономным затратам времени на расчет.