1.8.7 Работа четырехполюсника на нагрузку

Из основных уравнений четырехполюсника (1.123), видно что ток и напряжение на первичных зажимах состоят из двух слагающих, а именно:

; при;

; при. (1.153)

Если подставить (1.153) в (1.123), получим:

(1.154)

Уравнение (1.154) выражают основной принцип наложения в электрической цепи.

Рассмотрим теперь передачу энергии через пассивный четырехполюсник.

Определим соотношение между сопротивлением нагрузки и коэффициентамичетырехполюсника, при которых величина КПД будет максимальной, см. рисунок 1.66.

П

Рисунок 1.66 - Передача энергии через пассивный четырехполюсник

Из рисунка 1.66 видно, что:

- входная мощность на первичных зажимах;

- выходная мощность на вторичных зажимах.

Коэффициент полезного действия определится так

. (1.155)

Под КПД пассивного четырехполюсника понимается отношение мощности на входе к мощности на его выходе.

Запишем в функции от коэффициентов, имеем:

;

. (1.156)

Мощность на выходных зажимах будет

. (1.157)

Мощность на входных зажимах найдется

. (1.158)

Подставим в (1.158) выражение (1.156), получим, мощность на входе цепи

. (1.159)

Тогда КПД определится так:

;

. (1.160)

Величину сопротивления , при котором КПД имеет максимум определяется обычным образом. Из математики известно, что

, поэтому,

.

Знаменатель величина больше нуля, поэтому приравнивая числитель полученного выражения к нулю, имеем

, приводя подобные члены получаем

.

Окончательно можем записать

. (1.161)

1.8.8 Эквивалентные схемы четырехполюсников

Известно, что любой пассивный четырехполюсник с заданными первичными и вторичными зажимами характеризуется тремя независимыми постоянными коэффициентами.

Указанное позволяет представить пассивный четырехполюсник трехэлементными эквивалентными схемами.

Таких схем две, а именно: П-образная схема или П-схема; Т-образная схема или Т-схема.

Рассмотрим эти схемы подробнее.

Рисунок 1.67 - П-образная схема четырехполюсника

Эквивалентная схема «П», рисунок 1.67.

Дано: Коэффициенты пассивного четырехполюсника .

Найти: Элементы эквивалентной схемы.

Порядок расчета

1. Составляем расчетную схему для режима холостого хода. Схема изображена на рисунке 1.68.

Рисунок 1.68 - Режим холостого хода

2. Решаем П-образную схему для режима холостого хода.

Согласно расчетной схеме имеем

, отсюда:

; (1.162)

. (1.163)

3. Составляем расчетную схему для режима короткого замыкания, см. рисунок 1.69.

Рисунок 1.69 - Режим короткого замыкания

4. Решаем П-образную схему для режима короткого замыкания.

Согласно расчетной схемы имеем

, отсюда:

; (1.164)

;

. (1.165)

5. Проверяем результаты решения.

При правильном решении определитель из коэффициентов пассивного четырехполюсника должен быть равен единице.

В нашем случае имеем

6. Выражаем постоянные П-образной схемы через коэффициенты четырехполюсника.

Из соотношений (1.162) и (1.165) и учитывая (1.164) получаем:

; ;. (1.166)

Формулы (1.166) позволяют определять параметры П-образной схемы по известным коэффициентам пассивного четырехполюсника.

Анализируя (1.166) можно сделать выводы:

1. действительно, параметры зависят не от четырех, а лишь от трех коэффициентов четырехполюсника;

2. в случае симметричного четырехполюсника, как известно, , поэтому согласно (1.166) будет иметь

. (1.167)

Эквивалентная схема «Т», рисунок 1.70.

Рисунок 1.70 - Т-образная схема четырехполюсника

Дано: Коэффициенты пассивного четырехполюсника .

Найти: Элементы эквивалентной схемы.

Порядок расчета

1. Составляем расчетную схему для режима холостого хода. Схема изображена на рисунке 1.71.

Рисунок 1.71 - Режим холостого хода

2. Решаем Т-образную схему для режима холостого хода.

Согласно расчетной схеме имеем:

;

. (1.168)

А также:

;

. (1.169)

3. Составляем расчетную схему для режима короткого замыкания, рисунок 1.72.

Рисунок 1.72 - Режим короткого замыкания

4. Решаем Т-образную схему для режима короткого замыкания.

Согласно расчетной схемы имеем:

; . (1.170)

;

. (1.171)

5. Проверяем результаты решения.

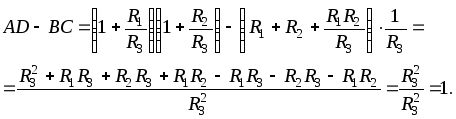
6. Выражаем постоянные Т-образной схемы через коэффициенты четырехполюсника.

Из выражений (1.168), (1.169) и (1.170) имеем:

; ;. (1.172)

Формулы (1.172) позволяют определять параметры Т-образной эквивалент­ной схемы по известным коэффициентам пассивного четырехполюсника.

Анализируя (1.172) можно сделать выводы:

1. действительно, параметры и здесь зависят не от четырех, а от трех коэффициентов четырехполюсника;

2. в случае симметричного четырехполюсника , поэтому согласно (1.172) будем иметь

. (1.173)

63