Порядок выполнения лабораторной работы

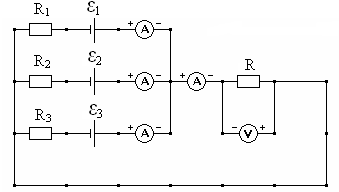
1. На экране монитора выберите раздел «Электричество и магнетизм», затем «Цепи постоянного тока».

Рис. 1

2. Соберите в окне «Цепи постоянного тока» на экране монитора эквивалентную цепь. Для этого переместите маркер мыши в нижнюю часть окна, щелкните левой кнопкой мыши на кнопку источника тока. Переместите маркер мыши на рабочую часть окна и расположите источники тока как показано на рис. 1.

3. Аналогично разместите другие элементы цепи (резисторы, амперметры, вольтметр и соединительные провода), предварительно нажав в нижней части окна соответствующую кнопку.

4. Установите значения ЭДС источников тока и сопротивления резисторов, указанные в таблице 1 для Вашей бригады. Для этого щелкните в нижней части окна левой кнопкой мыши на кнопку со стрелкой. Подведите маркер мыши к движку появившегося регулятора, нажмите левую кнопку и, удерживая ее, меняйте величину данного параметра.

5. Установите сопротивление резистора нагрузки R=1Ом. Измерьте значения всех токов и напряжение на нагрузке (щелкнув мышью на кнопку «Счет») и запишите их в таблицу 2. Меняя сопротивлениеRкаждый раз на 1 Ом, повторите измерения еще 5 раз. Полученные значение силы токов и напряжение запишите в таблицу 2.

6. Рассчитайте значения силы токов, используя правила Кирхгофа, и запишите в таблицу 3.

Таблица 1

Значения эдс источников тока и сопротивления резисторов

(не перерисовывать)

Бригада	1	2	3	4	5	6	7	8
ε 3 [В] ε 2 [В] ε3 [В]	3 7 -2	4 -3 -8	3 6 -4	6 -2 -8	-6 5 8	5 8 -4	-4 6 -7	8 -4 6
R1 [Ом] R2 [Ом] R3 [Ом]	2 1 1	1 3 1	2 1 2	1 1 2	2 1 1	1 2 1	1 1 2	1 3 1

Таблица 2

Результаты измерений

R [Ом]	I1 [A]	I2 [A]	I3 [A]	I [A]	U [B]
1
2
3
4
5
6

Таблица 3

Результаты расчета

R [Ом]	I1 [A]	I2 [A]	I3 [A]	I [A]
1
2
3
4
5
6

Контрольные вопросы

1. Дайте определение электрического тока.

2. Дайте определение силы тока, напишите единицы измерения силы тока.

3. Дайте определение электродвижущей силы источника тока и раскройте физический смысл ЭДС.

4. Сформулируйте закон Ома для однородного участка цепи.

5. Сформулируйте закон Ома для неоднородного участка цепи.

6. Сформулируйте законы Кирхгофа для разветвлённых цепей.

Лабораторная работа№304

МАГНИТНОЕ ПОЛЕ

Цель работы:

• знакомство с моделированием магнитного поля от различных источников

• экспериментальное подтверждение закономерностей для магнитного поля прямого провода и кругового витка (контура) с током

• экспериментальное определение величины магнитной постоянной.

Приборы и принадлежности:

• персональный компьютер

• компьютерные модели «Открытая физика 1.1».

Краткая теория

Магнитное поле – это частный вид электромагнитного поля. Оно создается неизменными во времени токами, протекающими по проводящим телам, неподвижным в пространстве.

Магнитное поле характеризуется индукцией , намагниченностьюи напряженностью магнитного поля. Эти величины связаны соотношением:

,

где –магнитная постоянная, равная,=1+–относительная магнитная проницаемость среды – она показывает, во сколько раз магнитная индукция поля, создаваемого током в данной среде, больше, чем в вакууме, – магнитная восприимчивость среды.

Магнитное поле изображается силовыми линиями магнитной индукции. Касательная к магнитной силовой линии в любой ее точке должна совпадать по направлению с силой магнитного поля, действующей в этой точке. Магнитные линии всегда замкнуты. Направление вектора определяется правилом правого винта:если поступательное движение буравчика совпадает с направлением тока, то направление вращения рукоятки буравчика укажет направление силовых линий магнитного поля прямолинейного проводника с током.

Магнитная индукция в какой-либо точке пространства зависит от формы проводников, по которым текут токи, образующие поле, от силы этих токов, от их направления, а также от расположения рассматриваемой точки относительно проводника. Характер этой зависимости определяется законом Био-Савара-Лапласа:магнитная индукция прямо пропорциональна току в проводнике и обратно пропорциональна расстоянию от проводника до точки, в которой измеряется магнитное поле.

(1)

где – векторное произведениеэлемента проводника с токоми вектораопределяющего положение точки, в которой измеряется магнитная индукция относительно элемента проводника с током. В скалярной форме (1) имеет вид:

. (2)

Вектор перпендикулярен к плоскости, содержащейинаправление его определяется правилом буравчика.

В Международной системе единиц физических величин (СИ) единицей индукции является тесла –1 Тл.

Рассчитаем, используя закон Био-Савара-Лапласа, магнитное поле, создаваемое бесконечным прямым проводником с током, и магнитное поле на оси кругового витка с током.

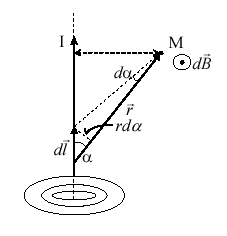
1. Рассмотрим магнитное поле, создаваемое бесконечным прямым проводником с током, в точке М, отстоящей на расстоянии а от проводника. Выделим элемент проводника(рис. 1). Пусть элемент виден из точки М под малым углом. Положение точки М относительно элементаопределяется вектором. Из рис. 1 видно, что

и . (3)

Используя закон Био-Савара-Лапласа, запишем индукцию магнитного поля, создаваемого элементом тока в точке М

. (4)

Подставив (3) в (4), получим

.

Ориентация вектора показана на рисунке. Для того, чтобы найти индукцию магнитного поля, создаваемого всем проводом, нужно, используя принцип суперпозиции, найти сумму векторовот всех элементов. Так как ориентация вектороводинакова, поэтому векторное суммирование можно заменить простым интегрированием по всему проводнику с током, т.е

.

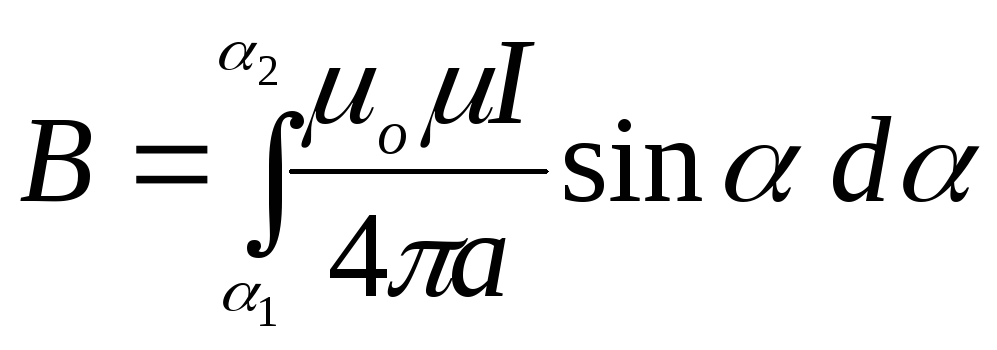Рис. 1

В случае бесконечного прямого тока α₁=0, α₂=π, тогда

.

В общем случае индукция магнитного поля, создаваемого прямым проводником с током конечной длины, равна

.

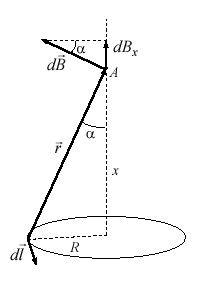
2.Возьмем на оси кругового витка точку А, отстоящую от плоскости витка на расстоянии х (рис. 2) и определим магнитное поле на оси кругового витка с током. Выделим на витке с током элемент тока. Ориентация вектора магнитной индукциисоздаваемого этим элементом, показана на рис. 2. Очевидно, что при суммировании векторовот всех элементов витка горизонтальные составляющие вектороввзаимно компенсируются, а вертикальные составляющиескладываются скалярно. Тогда индукция магнитного поля в точке А будет

Рис. 2

,

где S– длина витка,R– его радиус.

По закону Био-Савара-Лапласа,

(угол между векторами иравен π /2). Тогда индукция магнитного поля на оси кругового витка с током равна

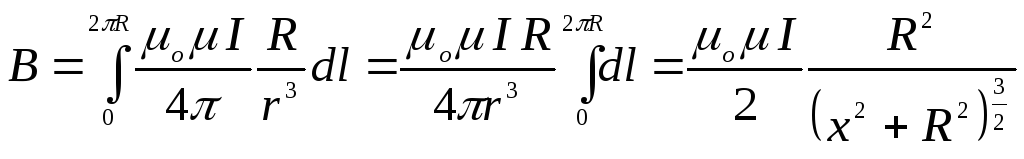
3. Рассмотрим магнитное поле, создаваемое соленоидом. Соленоидомназывают катушку цилиндрической или иной формы из проволоки, витки которой намотаны в одном направлении. Магнитное поле соленоида представляет собой результат сложения полей, создаваемых круговыми токами, расположенными вплотную и имеющими общую ось.

Рассмотрим бесконечно длинный соленоид, по которому течет ток Iи который имеетnвитков на единицу длины. Распределение магнитной индукции по длине соленоида вдоль его оси описывается выражением

.

Для бесконечно длинного соленоида в каждой точке на его оси ₁= 180⁰,₂= 0⁰. Подставляя значения₁и_2, получаем выражение для магнитной индукции на оси бесконечно длинного соленоида:

.

Зная геометрические параметры соленоида (длину lи диаметр виткаd), можно рассчитать₁и₂, а следовательно, иВдля любой точки оси соленоида. Для центра соленоида выражение дляВимеет наиболее простой вид (в этом случае₁= 180⁰-₂): В = В соs₂.

Из геометрических соображений

.

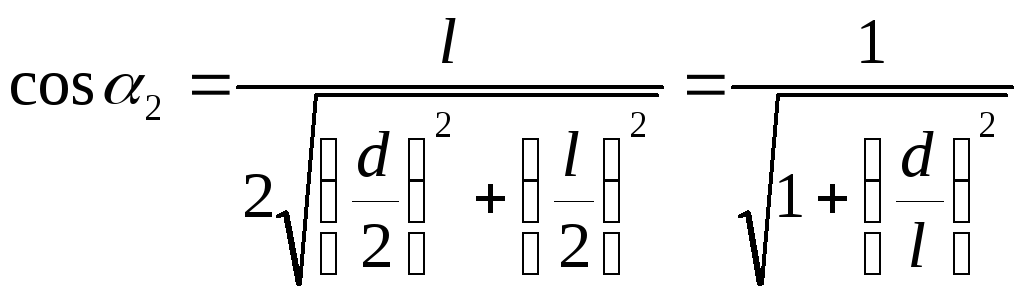Тогда

.
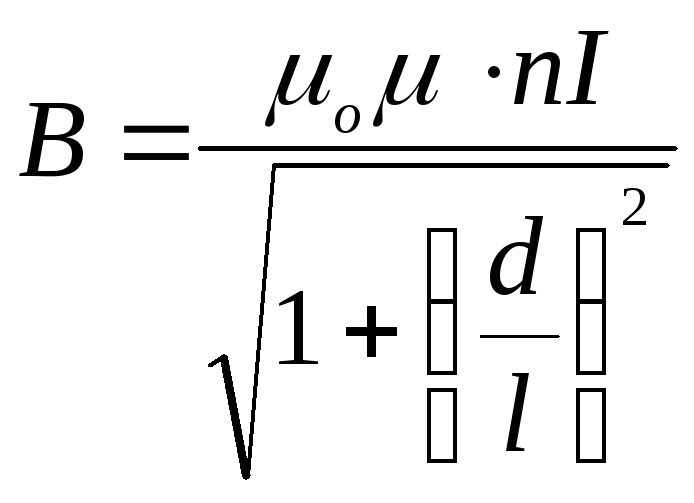