
- •Лабораторный практикум по физике с компьютерными моделями
- •Часть II
- •«Электричество и магнетизм»
- •Введение
- •Раздел III, IV
- •Порядок выполнения лабораторной работы
- •Напряженность электрического поля конденсатора
- •Результаты измерений
- •Контрольные вопросы
- •Лабораторная работа № 302 взаимодействие электрических зарядов
- •Краткая теория
- •Порядок выполнения лабораторной работы
- •Результаты измерений
- •Контрольные вопросы
- •Лабораторная работа №303 цепи постоянного тока
- •Краткая теория
- •Порядок выполнения лабораторной работы
- •Значения эдс источников тока и сопротивления резисторов
- •Результаты измерений
- •Результаты расчета
- •Порядок выполнения работы
- •Результаты измерений
- •Контрольные вопросы
- •Лабораторная работа №305 электромагнитная индукция
- •Краткая теория
- •Порядок выполнения работы
- •Значения индукции магнитного поля b, сопротивления r и скоростей υ
- •Результаты измерений
- •Контрольные вопросы
- •Свободные колебания в rlc - контуре
- •Краткая теория
- •Порядок выполнения лабораторной работы
- •Значения ёмкости конденсатора и индуктивности катушки
- •Результаты измерений
- •Контрольные вопросы
- •Вынужденные колебания в rlc – контуре
- •Краткая теория
- •Порядок выполнения лабораторной работы
- •Значения характеристик
- •Результаты измерений
- •Вопросы и задания для самоконтроля
- •Содержание
- •Лабораторный практикум по физике с компьютерными моделями
- •Часть II
- •Компьютерная верстка о.Л. Никонович
Лабораторная работа № 302 взаимодействие электрических зарядов
Цель работы:
знакомство с моделированием электрического поля от точечных источников
экспериментальное подтверждение закономерностей для электрического поля точечного заряда и электрического диполя
экспериментальное определение величины электрической постоянной.
Приборы и принадлежности:
персональный компьютер
компьютерные модели «Открытая физика 1.1».
Краткая теория
Электрический заряд– величина, определяющая интенсивность электромагнитного взаимодействия заряженных частиц. В системе единиц измерения СИ измеряется вкулонах (Кл)..Электрические заряды обладают следующими свойствами:
Полный электрический заряд изолированной системы сохраняется (аддитивность).
Электрический заряд релятивистки инвариантен, т. е. его величина одинакова при измерении в любой инерциальной системе отсчета.
Величина заряда может принимать только дискретные значения:
– минимальный
заряд частицы
![]() =
1,60·10-19Кл;
=
1,60·10-19Кл;
– любой заряд q
кратен минимальному, т.е.
![]() ,гдеN – целое
,гдеN – целое
число;
– минимальные положительный и отрицательный заряды равны
по абсолютной величине.
Точечным электрическим зарядомназывается заряженное тело, линейные размеры которого несущественны в данной задаче. Всякое заряженное тело можно рассматривать как совокупность точечных зарядов.
Если заряды распределены в заряженном теле непрерывно – вдоль некоторой линии (например, в случае заряженного тонкого стержня), поверхности (например, в случае заряженного проводника) или объема, пользуются понятиями линейной, поверхностной и объемной плотности зарядов.
Линейная плотность
электрических зарядов
![]() ,
где
,
где![]() –
заряд малого участка заряженной линии
длиной
–
заряд малого участка заряженной линии
длиной![]() .
Поверхностная плотность электрических
зарядов
.
Поверхностная плотность электрических
зарядов![]() ,
где
,
где![]() –
заряд малого участка заряженной
поверхности площадью
–
заряд малого участка заряженной
поверхности площадью![]() .
Объемная плотность электрических
зарядов
.
Объемная плотность электрических
зарядов![]() ,
где
,
где![]() –
заряд малого элемента заряженного тела
объемом
–
заряд малого элемента заряженного тела
объемом![]() .
.
Электростатическое поле– это частный вид электромагнитного поля. Оно создается совокупностью электрических зарядов, неподвижных в пространстве и неизменных во времени.
Удаленные друг от друга точечные заряды в электростатическом поле взаимодействуют по закону Кулона:
Два точечных
заряда q1
и q2
взаимодействуют друг с другом с силой
![]() ,
прямо пропорциональной произведению
зарядовq1
и q2 и
обратно пропорциональной квадрату
расстояния r между
ними. Эта сила направлена по линии,
соединяющей точечные заряды.
,
прямо пропорциональной произведению
зарядовq1
и q2 и
обратно пропорциональной квадрату
расстояния r между
ними. Эта сила направлена по линии,
соединяющей точечные заряды.
![]() ,
(1)
,
(1)
где r– расстояние между двумя точечными
зарядамиq1иq2,![]() –
радиус - вектор, соединяющий зарядq2
с зарядом q1,
–
радиус - вектор, соединяющий зарядq2
с зарядом q1,![]() –
электрическая постоянная, она равна
–
электрическая постоянная, она равна![]() ,
,![]() – диэлектрическая проницаемость среды
– она показывает, насколько сила
взаимодействия между двумя точечными
зарядами в вакууме больше силы
взаимодействия между двумя точечными
зарядами в данной среде.
– диэлектрическая проницаемость среды
– она показывает, насколько сила
взаимодействия между двумя точечными
зарядами в вакууме больше силы
взаимодействия между двумя точечными
зарядами в данной среде.
Напряженность– векторная физическая величина (![]() ),
определяющаяся отношением силы
),
определяющаяся отношением силы![]() ,
действующей со стороны поля на неподвижный
положительный точечный электрический
заряда
,
действующей со стороны поля на неподвижный
положительный точечный электрический
заряда![]() помещенный в рассматриваемую точку
поля, к величине этого заряда:
помещенный в рассматриваемую точку
поля, к величине этого заряда:
![]() (2)
(2)
В системе единиц
измерения СИ напряженность измеряется
в
![]() (Вольт на метр).
(Вольт на метр).
Простейшей системой
точечных зарядов является электрический
диполь. Электрическим диполемназывается совокупность равных по
величине, но противоположных по знаку
двух точечных зарядов– qи+ q,
находящихся друг относительно друга
на некотором расстоянии. Вектор,
направленный по оси диполя (прямая,
проходящая через оба заряда) от
отрицательного к положительному и
равный расстоянию между ними, называется
плечом диполя![]() .
Вектор
.
Вектор![]() совпадающий по направлению с плечом
диполя и равный произведению зарядаqна плечоl, называетсяэлектрическим моментом диполяили
дипольным моментом,
совпадающий по направлению с плечом
диполя и равный произведению зарядаqна плечоl, называетсяэлектрическим моментом диполяили
дипольным моментом,![]() .
Если длинаlпренебрежимо
мала по сравнению с расстоянием от
диполя до точки наблюдения, то диполь
называется точечным.
.
Если длинаlпренебрежимо
мала по сравнению с расстоянием от
диполя до точки наблюдения, то диполь
называется точечным.
Напряженность электростатического поля точечного диполя можно найти в соответствии с принципом суперпозиции, согласно которому напряженность результирующего поля, создаваемого системой зарядов, равна сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
![]() ,
(3)
,
(3)
где
![]() и
и![]() – напряженности полей, создаваемых
соответственно положительным и
отрицательным зарядамиq.
– напряженности полей, создаваемых
соответственно положительным и
отрицательным зарядамиq.
Рассчитаем напряженность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.
1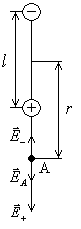 .
Напряженность поля на продолжении оси
диполя в точкеАв соответствии с принципом суперпозиции
полей равна
.
Напряженность поля на продолжении оси
диполя в точкеАв соответствии с принципом суперпозиции
полей равна![]() .
Согласно формуле (2), напряженность в
точкеАможно
записать:
.
Согласно формуле (2), напряженность в
точкеАможно
записать:
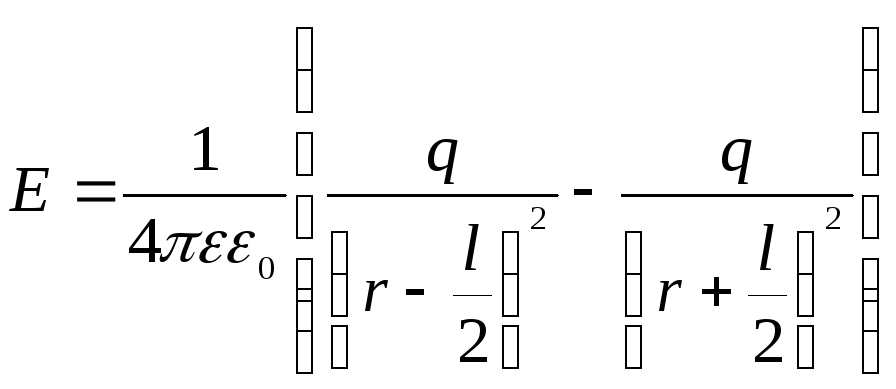 ,
,
где r – расстояние от середины оси диполя до точкиА. Так как для поля диполяl2<<r2, то напряженность
![]() .
(4)
.
(4)
2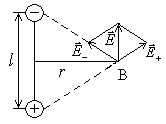 .
Напряженность поля на перпендикуляре,
восстановленном к оси из его середины
в точке В (точкаВ
равноудалена от зарядов), равна
.
Напряженность поля на перпендикуляре,
восстановленном к оси из его середины
в точке В (точкаВ
равноудалена от зарядов), равна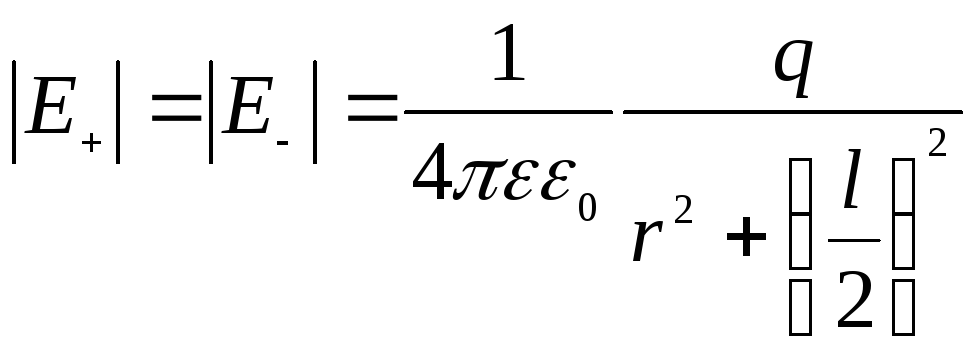 .
(5)
.
(5)
Из подобия
равнобедренных треугольников, опирающихся
на плечо диполя и вектор
![]() ,
получим:
,
получим:
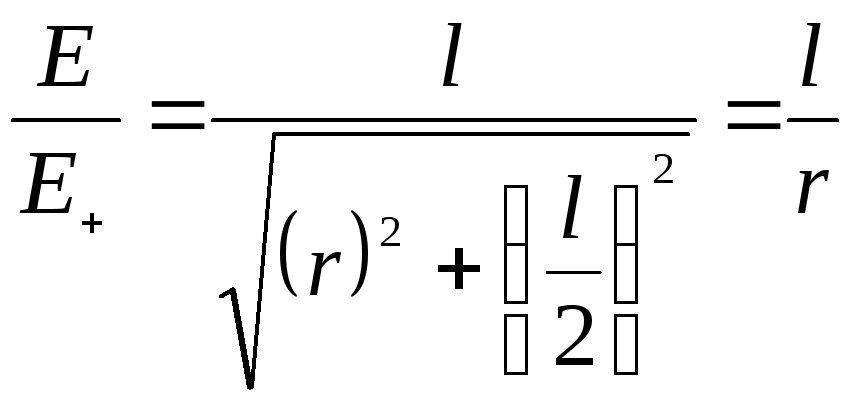 .
(6)
.
(6)
Поставив в выражение
(6) значение
![]() из выражения (5), получим
из выражения (5), получим
![]() .
(7)
.
(7)
