
matem-ege-shpora / математика С4
.pdf
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А.
l |
A A |
|
|
a2 (R r)2 |
(длина внешней |
|||||||
1 |
|
1 |
2 |
|
|
касательной) |
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
2 |
B B |
2 |
|
|
a2 (R r)2 (длина внут- |
||||||
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
ренней касательной). |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Ответ: |
a2 (R r)2 или |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 (R r)2 . |
||
расположение центров окружностей относительно их общей точки касания
В условии задачи этого типа фигурируют две окружности, но не указан тип касания (внешний или внутренний, см.
рис. 16).












 r
r  O2
O2 
R A










O1 


 O1
O1







Рис. 16
При любом способе касания точка касания и центры окружностей лежат на одной прямой.
При внешнем касании центры окружностей расположены на линии центров по разные стороны от точки касания, при внутреннем – по одну сторону.
Расстояние между центрами касающихся окружностей радиусов R и r (R r ) равно R r при внешнем касании и R r при внутреннем.
Пример 17. (ЕГЭ 2010). Окружности радиусов 2 и 4 касаются в точке B . Через точку B проведена прямая, пересекающая второй раз меньшую окружность в точке A, а большую – в точке
C . Известно, что AC 3
 2 . Найдите
2 . Найдите
BC.
Решение. Поскольку в условии не сказано о типе касания окружностей (внешнее или внутреннее), то рассмотрим два случая.
1. Если окружности касаются внешним образом, то проведем через точку B об-
05.01.2011.
щую касательную KK1 (она перпендикулярна линии центров, см. рис. 17а).
Треугольники AO2B и O1BC подобны по первому признаку подобия. В этих треугольниках O2BA O1BC, как вер-
тикальные; AO2B BO1C как центральные углы, опирающиеся на дуги, имеющие равную меру. ABK1 KBC, как вертикальные, и каждый из этих углов – угол между хордой и касательной. Следовательно, соответствующие дуги имеют равную меру.
C 

K


 O2
O2


 B O1
B O1
A 


 K1
K1 










Рис. 17а
Для подобных треугольников AO2B и O1BC можем записать
AB BO2 2 1.
BC BO1 4 2
Отсюда
BC 2 AC 2 3
 2 2
2 2
 2. 3 3
2. 3 3

 C
C








 A
A
B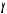
O2 
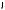 O1
O1
Рис. 17б
2. Окружности касаются внутренним образом (см. рис. 17б). В этом случае при исходных числовых данных задача не имеет решения (докажите самостоятельно).
Ответ: 2
 2.
2.
11
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. |
05.01.2011. |
Пример 18. Окружности S1 и S2 радиусов R и r (R r ) соответственно касаются в точке A. Через точку B , лежащую на окружности S1, проведена прямая, касающаяся окружности S2 в точке M . Найдите BM , если известно, что AB a.
Решение. Возможны два случая расположения указанных окружностей в зависимости от типа касания.
1. Пусть окружности касаются внешним образом (см. рис. 18).
|
B |
M |
R |
|
|
a |
r |
|
|
|
|
|
O2 |
|
O1 |
R A |
Рис. 18
1-й способ решения. Пусть O1 и O2
центры окружностей S1 и S2 соответст-
венно, а O1 AB |
|
(см. рис. 18). По |
|||||||||||
теореме |
косинусов |
|
для |
|
|
треугольника |
|||||||
O1AB: |
|
|
|
|
|
|
|
|
|
|
|
|
|
O B2 |
O A2 AB2 |
|
2O A ABcos |
||||||||||
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 R2 a2 |
2Racos . |
|
|
|
||||||||
Отсюда получим cos |
|
|
a |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2R |
|
|
|
|
||
Теперь используем теорему косинусов |
|||||||||||||
для треугольника O2AB: |
|
|
|
|
|
|
|
|
|||||
O2B2 |
O2 A2 AB2 2O2 A ABcos |
||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
O2B2 r2 a2 |
2r acos . |
|
|
||||||||||
Подставив cos |
|
a |
|
в последнее ра- |
|||||||||
|
|
|
|||||||||||
|
|
2R |
|
|
|
|
|
|
|
|
|||
венство, получим O2B |
2 |
r |
2 |
a |
2 |
|
a2r |
||||||
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
В прямоугольном треугольнике O2BM
( BMO2 |
90 ), используя теорему Пи- |
||||||||||
фагора, находим BM2 |
O B2 r2 |
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
a2r |
2 |
|
2 |
r |
||
r |
|
a |
|
|
|
r |
|
a |
1 |
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
R |
|
|
|
R |
||
Отсюда BM a |
1 |
r |
. |
|
|||
|
|
R |
|
2-й способ решения. Продолжим АВ до пересечения с окружностью S2 в точке
E (см. рис. 19). Треугольники AO1B и AO2E равнобедренные и подобные, так
как |
O1AB EAO2 . |
Следовательно, |
||||||||
|
AE |
|
|
r |
|
и AE |
ar |
. |
|
|
|
|
|
R |
|
|
|||||
|
AB |
|
|
|
R |
|
||||
|
|
|
|
B |
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
a |
||
|
|
|
|
|
|
R |
|
|
||
|
|
|
|
|
|
|
|
|
r O2 |
|
|
|
|
|
|
|
|
O1 R A |
|||
|
|
|
|
|
|
|
r |
|||









 E
E
Рис. 19
По теореме о секущей и касательной имеем
BM 2 BA BE, |
|
|
|
|
|
|
||||||||
BM 2 |
BA (BA AE) , |
|||||||||||||
|
|
2 |
|
|
|
ar |
|
|
|
|
|
|
||
BM |
|
a |
a |
|
|
|
, |
|
|
|
|
|||
|
R |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ar |
|
|
|
|
|
|
r |
|
||
BM a |
a |
|
|
a |
|
1 |
|
. |
||||||
|
|
|
||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
R |
|||
2. Пусть окружности касаются внутренним образом (см. рис. 20). Тогда, проводя аналогичные вычисления, получим
BM a 1 r .
R
B

 a
a 
O1
M

 rO2
rO2


 A
A
Рис. 20
Ответ: a 1 r R
12
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А.
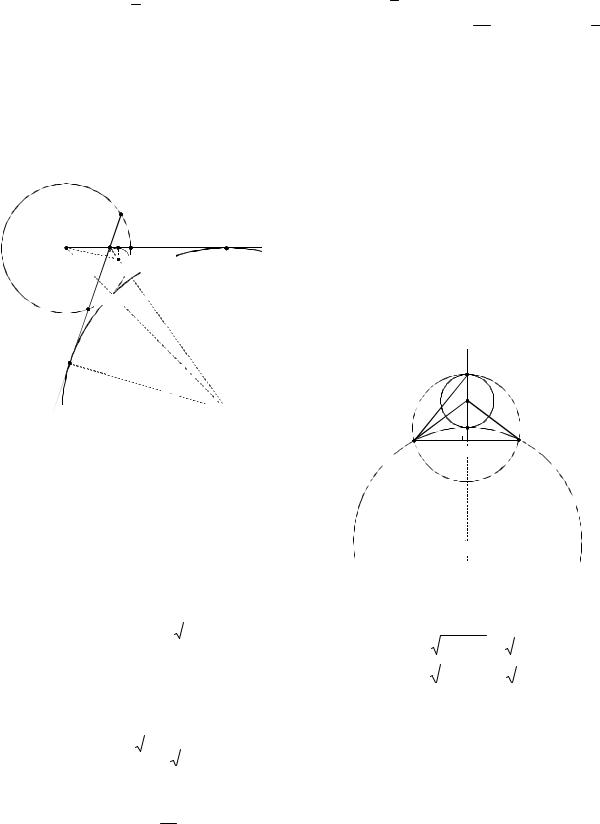
Пример 19. Дана окружность радиуса 2 с центром О. Хорда АВ пересекает радиус ОС в точке D, причемCDA 120 . Найдите радиус окружности, вписанной в угол ADC и касающейся дуги АС, если OD 
 3.
3.
Решение. Возможны два случая расположения указанной окружности в зависимости от типа касания с данной окружностью. В обоих случаях центры O1 и O2 этих окружностей будут лежать на биссектрисе угла ADC (см. рис. 21).
\ |
|
B |
|
D E C |
E1 |
O 


 L
L O
O
 1
1

 H
H




A 






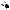
 O2
O2
Рис. 21
1. Рассмотрим внутреннее касание окружностей. Пусть радиус искомой окружности с центром в точке O1 равен r. E – точка касания этой окружности с радиусом OC . В прямоугольном треуголь-
нике DEO1 EDO1 |
60 |
|
(O1D бис- |
||||||||
сектриса угла ADC) |
|
|
|
|
|
|
|
|
|
|
|
DE r ctg60 |
r |
|
. |
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
3 |
|
|
||||
Используя теорему о секущей и каса- |
|||||||||||
тельной, получим |
|
|
|
|
|
|
|
|
|
|
|
OL OH OE2 , |
|
|
|||||||||
|
|
|
|
|
r |
2 |
|||||
|
|
|
|
||||||||
(2 2r) 2 |
|
3 |
|
|
|
|
|
|
, |
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
||||
r2 18r 3 0.
Условию задачи удовлетворяет поло-
жительный корень r 2
 21 9.
21 9.
05.01.2011.
2. В случае внешнего касания искомая окружность радиуса R с центром в точке O2 касается продолжений сторон DC и DA и данной окружности. Тогда, проводя аналогичные вычисления, получим
R 3 2
 3.
3.
Ответ: 2
 21 9 или 3 2
21 9 или 3 2
 3.
3.
Пример 20. Вершина равнобедренного треугольника с боковой стороной 5 и основанием 8 служит центром данной окружности радиуса 2. Найдите радиус окружности, касающейся данной и проходящей через концы основания треугольника.
Решение. Пусть D – середина основания AC данного треугольника ABC. Обозначим через E и F точки пересечения прямой BD и окружности радиуса 2 с центром в точке B . Тогда (см. рис. 22):
AD 4, |
BD 3, ED 1, FD 5. |
|
Из теоремы |
Пифагора для прямо- |
|
|
|
F |
|
|
B |
A |
|
E |
|
C |
|
D
 O2
O2
Рис. 22
угольных треугольников AED и AFD соответственно имеем:
|
|
|
AE |
42 12 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
17, |
||||||||||||
|
|
|
AF |
42 52 |
|
|
|
|
. |
||||||||
|
|
|
41 |
||||||||||||||
Находим |
|
|
|
площади |
|
|
|
|
треугольников |
||||||||
AEC и AFC : |
|
|
|
|
|
|
|
|
|
||||||||
S |
AEC |
|
1 |
AC ED |
1 |
8 1 4, |
|||||||||||
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|||||||
S |
AFC |
|
1 |
AC FD |
|
1 |
8 5 20. |
||||||||||
2 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Возможны два случая расположения указанной в условии окружности в зависимости от типа касания с данной окруж-
13
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. |
05.01.2011. |
ностью. В обоих случаях центры O1 и O2 этих окружностей будут лежать на биссектрисе угла – прямой BD (см. рис. 22).
1. Пусть окружности касаются внешним образом. Тогда искомая окружность описана около треугольника AEC. Найдем ее радиус по формуле
R AE EC AC 17 8 17.
4SAEC |
4 4 |
2 |
2. Пусть окружности касаются внутренним образом. Тогда искомая окружность описана вокруг треугольника AFC . Найдем ее радиус
R |
AF FC AC |
|
41 8 |
|
41 |
. |
|
4 20 |
|
||||
|
4SAFC |
10 |
|
|||
Ответ: 17 или 41. 2 10
расположение центров окружностей относительно общей хорды
В условии задачи этого типа фигурируют две пересекающиеся окружности, но не указано расположение центров окружностей относительно их общей хорды
(см. рис. 23а и 23б).

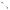 A
A
R 


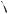
 r
r
O1  C
C  O2
O2

 B
B
Рис. 23а



 A
A

 R
R
r 


 O1 O2 C
O1 O2 C 
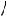

 B
B
Рис. 23б
Пересекающиеся окружности в точках А и В имеют общую хорду АВ.
Общая хорда перпендикулярна линии центров и делится ею пополам.
Пример 21. Окружности радиусов 10 и 17 пересекаются в точках А и В. Найдите расстояние между центрами окружностей, если AB 16.
Решение. Отрезок AB – общая хорда данных окружностей. В условии не указано расположение центров окружностей относительно AB . Поэтому задача допускает два вида чертежа.
1. Пусть центры окружностей лежат по разные стороны от их общей хорды AB (см. рис. 23а). Линия центров O1O2 перпендикулярна хорде AB и делит ее в точке пересечения C пополам. Это следует из равенства треугольников O1 AO2
и O1BO2 по трем сторонам и совпадения оснований высот, опущенных из точек A и B . Тогда из прямоугольных треугольников O1 AC и O2 AC соответственно получаем:
O1C 
 172 82 15
172 82 15
и
O2C 
 102 82 6.
102 82 6.
Искомое расстояние между центрами равно
O1O2 O1C O2C 15 6 21.
2. Пусть центры окружностей лежат по одну сторону от хорды AB (см. рис. 23б). Аналогично поступая, находим
O1O2 O1C O2C 15 6 9.
Ответ: 21 или 9.
Пример 22. Окружности с центрами O1 и O2 пересекаются в точках А и В.
Известно, что AO1B 90 , AO2 B60 , O1O2 a. Найдите радиусы окружностей.
Решение. Отрезок AB – общая хорда данных окружностей. В условии не указано расположение центров окружностей относительно AB . Поэтому задача допускает два вида чертежа.
14
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А.
A |
R |
|
A |
|
r |
O2 |
Rr |
||
|
||||
O1 C |
O2 |
|
O1 C |
|
B |
|
|
B |
|
а |
Рис. 24 |
|
б |
|
|
|
|
1. Пусть центры окружностей лежат по разные стороны от их общей хорды AB (см. рис. 24а). Так как треугольники AO1B и AO2B равнобедренные, то линия
центров |
является биссектрисой |
углов |
AO1B и AO2B. Получаем |
|
|
AO1C 45 , AO2C 30 . |
|
|
Пусть |
AC x. Треугольник |
AO1C |
прямоугольный, AO1C CAO1 |
45 . |
|
Значит O1C AC x. Для треугольника
AO2C имеем
|
O2C AC ctg30 x 3. |
|
|
|
|||||||||||||||
Тогда |
|
|
O1O2 |
O1C O2C |
|
или |
|||||||||||||
a x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
. |
||
|
3. Отсюда находим x |
|
|||||||||||||||||
|
|
|
|
||||||||||||||||
|
3 1 |
||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
, |
|
|
|
|
||||
|
|
O A x |
|
2 |
|
|
|
||||||||||||
|
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
3 1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
O2 A 2AC 2x |
|
2 |
a |
. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 1 |
|
|
|
|||||
2. Пусть центры окружностей лежат по одну сторону от хорды АВ (см. рис. 24б). Проводя аналогичные рассуждения, получим
O A |
a |
2 |
, O |
A |
|
|
2 |
a |
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
3 1 |
2 |
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Ответ: |
a |
|
|
|
|
|
|
|
|
|
|
|
|
2a |
||||||||||||
|
|
|
2 |
, |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
3 1 |
|
|
|
|
|
3 1 |
|||||||||||||
|
|
|
|
|
|
|
a |
|
|
, |
|
2 |
a |
. |
|||||||||||||||
|
|
|
|
|
или |
|
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
3 1 |
|
|
|
|
3 1 |
|||||||||||||||
05.01.2011.
расположение центров окружностей относительно хорды большей окружности
В условии задачи следующего типа фигурируют две окружности, одна из которых расположена внутри другой и касается хорды окружности большего радиуса (см. рис. 25).
O2 |
N |
|
A B |
N |
A |
B |
|
C |
O2 |
M O1 |
C |
M |
O1 |
|
|
|
|||
|
|
|
а б
Рис. 25
Вычисления в этой задаче сводятся к применению теоремы Пифагора в треугольнике О1О2С, при этом расстояние О1А находится из теоремы Пифагора для треугольника МАО1 (см.
рис. 25а, б).
Пример 23. Окружности радиусов 20 и 3 касаются внутренним образом. Хорда AB большей окружности касается меньшей окружности в точке M . Найдите длины отрезков AM и MB , если
AB 32.
E |
O1 N |
|
A |
B |
|
M |
|
|
C |
O |
|
Рис. 26а
Решение. Пусть точка N – середина хорды AB , тогда расстояние от центра O окружности радиуса 20 до хорды AB равно
ON OB |
2 |
|
AB |
2 |
|
|
|
|
|
12. |
|
|
|
||||
|
|
|
2 |
|
|
Рассмотрим два случая.
15
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А.
1. Центры O и O1 окружностей расположены по разные стороны относительно хорды AB (см. рис. 26а), O1M 3.
Продолжив перпендикуляр O1M к
хорде |
AB за точку M и опустив на него |
|
перпендикуляр из центра O, получим |
||
прямоугольный треугольник OO1C, в ко- |
||
тором |
OO1 17, |
O1C O1M MC |
O1M ON 15 и |
OC MN . Тогда из |
|
теоремы Пифагора для треугольника OO1C получаем
OC 
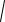 OO12 O1C2
OO12 O1C2 
 172 152 8.
172 152 8.
Тогда
AM AN MN 16 8 8
и
MB MN NB 8 16 24.
A

 M N
M N 
 B
B
E






 O1
O1


 C
C



O
Рис. 26б
2. Центры O и O1 окружностей расположены по одну сторону относительно хорды AB (см. рис. 26б). Тогда из теоремы Пифагора для треугольника OO1C получаем
|
|
|
|
|
OC OO2 |
O C2 |
172 92 4 13. |
||
1 |
1 |
|
|
|
Тогда AM AN MN 16 4
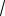 13 и
13 и
MB MN NB 4
 13 16.
13 16.
Замечание. В данной задаче можно рассмотреть еще два случая, когда точка касания M расположена правее точки N . В этом случае ответы будут AM 24
и MB 8 или |
AM 16 4 13 и |
MB 16 4
 13 .
13 .
Ответ: 24 и 8; 16 4
 13 и 16 4
13 и 16 4
 13.
13.
05.01.2011.
Пример 24. Расстояние между центрами двух окружностей равно 5r . Одна из окружностей имеет радиус r, а вторая – 7r. Хорда большей окружности касается меньшей окружности и делится точкой касания в отношении 1:6. Найдите длину этой хорды.
Решение. Воспользуемся рисунком 25.
Пусть хорда |
MN 7x. Тогда расстояние |
||||||||||||
от центра O1 |
равно |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MN 2 |
|
|
|
|
|
|||
|
|
|
2 |
|
|
2 |
|
x2 |
|||||
O A MO |
|
|
|
7 r |
|
|
|
, |
|||||
|
|
|
4 |
||||||||||
1 |
|
1 |
|
2 |
|
|
|
|
|||||
а AB AN NB 7x x 5x . 2 2
Рассмотрим два случая.
1. Центры O1 и O2 окружностей расположены по разные стороны относи-
тельно хорды MN . Так как O1O2 |
5r , |
||||||||||||||||||||||||||||||||||||
O2B r , |
|
|
то, продолжив перпендикуляр |
||||||||||||||||||||||||||||||||||
O2B к хорде MN за точку B и опустив |
|||||||||||||||||||||||||||||||||||||
на него перпендикуляр из O1 , получим |
|||||||||||||||||||||||||||||||||||||
прямоугольный |
|
|
треугольник |
|
|
O1O2C, |
в |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
котором O2C O2B BC r 7 |
|
|
|
r |
2 |
|
x2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и O1C AB. Тогда из теоремы Пифагора |
|||||||||||||||||||||||||||||||||||||
для треугольника O1O2C получаем |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
OC2 OO2 |
O C2 |
или |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
25x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
25r |
2 |
r 7 r2 |
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возводя в квадрат выражение, стоя- |
|||||||||||||||||||||||||||||||||||||
щее в скобках, получаем уравнение |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6x |
2 |
|
25r |
2 |
14r r |
2 |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
или |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
251x |
2 |
r |
2 |
429r |
4 |
|
0, |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
36x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
25r |
2 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
6x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Последняя система не имеет решения, |
|||||||||||||||||||||||||||||||||||||
так |
как |
корни |
|
|
уравнения |
|
|
x1 |
r |
|
|
|
и |
||||||||||||||||||||||||
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|||||||||||||||||||||||||||
x2 |
|
143 |
|
не |
удовлетворяют |
|
условию |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
6
6x2 25r2 0.
Это значит, что такой случай невозможен.
16
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А.
2. Центры O1 и O2 окружностей расположены по одну сторону относительно хорды MN . Так как O1O2 5r , O2B r , то, опустив на отрезок O1A перпендику-
ляр из центра O2 , получим прямоуголь-
ный |
треугольник O1O2C, |
в |
котором |
|||||
|
|
|
|
|
|
|
|
|
O C |
AO |
AC 7 r |
2 |
|
x2 |
r |
и |
|
|
|
|||||||
1 |
1 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||
O2C AB. Тогда из теоремы Пифагора для треугольника O1O2C получаем
|
|
CO2 |
OO2 |
OC2 |
или |
|||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
1 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
25x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|||||||
|
|
25r2 |
|
7 r2 |
|
|
|
r . |
||||||||||||||||||
4 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Возводя в квадрат выражение, стоя- |
||||||||||||||||||||||||||
щее в скобках, получаем уравнение |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
25r |
2 |
6x |
2 |
14r r |
2 |
|
|
|
x2 |
||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 |
251x |
2 |
r |
2 |
429r |
4 |
|
|
0, |
|||||||||||||
|
36x |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
6x |
2 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
25r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Получаем |
два |
|
решения |
|
|
x1 r |
|
и |
||||||||||||||||||
|
|
|
3 |
|||||||||||||||||||||||
x2 |
|
143 |
r. Отсюда находим два значе- |
|||||||||||||
|
||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
r и MN |
7 |
|
|
|
|
r . |
||||||||
ния MN 7 |
|
143 |
||||||||||||||
3 |
||||||||||||||||
|
6 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
r и |
7 |
|
|
r. |
|||||
|
|
|
|
|
Ответ: 7 |
|
|
143 |
||||||||
|
|
|
|
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
6
Пример 25. (ЕГЭ, 2010). В окружно-
сти, радиус которой равен 15, проведена хорда AB 24. Точка С лежит на хорде АВ так, что AC : BC 1:2. Найдите радиус окружности, касающейся данной окружности и касающейся хорды АВ в точке С.
Решение. Возможны два случая расположения указанной окружности (см. рис. 27). Центры этих окружностей O1 и O2 будут лежать на перпендикуляре к хорде AB , проходящем через точку C .
1. Пусть точки O и O1 , где O центр данной окружности, а O1 центр окружности, указанной в условии, лежат по разные стороны относительно прямой
AB .
|
|
|
|
|
|
05.01.2011. |
|
Так как |
AC : BC 1:2, |
то AC 8. |
|||||
Пусть N середина хорды AB . Тогда из |
|||||||
прямоугольного треугольника ONB по- |
|||||||
лучаем |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ON OB2 NB2 152 122 9. |
|||||||
|
|
E1 |
O1 N |
|
|
||
A |
C |
B |
|||||
|
|
|
|
|
|
|
|
|
|
K |
|
O |
|
|
|
E2 |
O2 |
|
|
|
|||
|
|
|
|
|
|
||
Рис. 27
Пусть K середина хорды, перпендикулярной AB и проходящей через точку C . Четырехугольник KCNO – прямоугольник,
OK CN AN AC 12 8 4.
Пусть искомый радиус равен r. Так как центры O, O1 и точка касания E1 лежат на одной прямой, то
OO1 OE1 O1E1 15 r.
Из теоремы Пифагора для прямо-
угольного треугольника KO1O , |
в кото- |
|
ром OK 4, |
OO1 15 r и |
KO1 |
KC CO1 9 r , получаем
OO12 OK2 KO12
или
(15 r)2 42 (9 r)2 .
Отсюда r 8 . 3
2. Точки O и O2 лежат по одну сторону относительно прямой AB (см. рис. 27). В этом случае из теоремы Пифагора для прямоугольного треугольника KO2O,
в котором OK 4, |
OO2 15 r |
и |
|||||
KO2 CO2 KC r 9, |
получаем |
||||||
r |
32 |
. |
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
8 |
|
32 |
|
|
|
|
|
Ответ: |
и |
. |
||
|
|
|
3 |
|
3 |
|
|
17
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А.
расположение точек касания окружности и прямой
Пример 26. На стороне ВА угла ABC, равного 30°, взята такая точка D, что AD 2 и BD 1. Найдите радиус окружности, проходящей через точки А, D и касающейся прямой ВС.
Решение. Центр искомой окружности O – точка пересечения серединного перпендикуляра к отрезку AD и перпендикуляра к прямой ВС, восставленного из точки касания E (см. рис. 28) окружности и прямой. Возможны два варианта положения окружности. В первом случае окружность касается луча BC, во втором точка касания E1 лежит на продолжении луча BC за точку B .
O1

 O
O


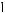
D


 E1
E1
 E G
E G
Рис. 28
1. Пусть точка касания лежит на луче ВС. Тогда по теореме о касательной и секущей имеем
BE2 BD AB 1 3 3,
откуда BE 3. |
|
|
|||
В треугольнике |
BDE |
DBE 30 , |
|||
BD 1, |
BE |
|
|
||
3. Тогда из теоремы ко- |
|||||
синусов |
получаем |
DE2 DB2 BE2 |
|||
2 DB BE cos( ABE) 1, |
т.е. DE 1. |
||||
Так как BD DE, то треугольник BDE – |
|||||
равнобедренный и |
BED 30 . По- |
||||
скольку этот угол образован касательной BE и хордой DE , то дуга окружности DE равна 60 . Следовательно, искомый радиус окружности равен хорде DE 1.
05.01.2011.
Тогда центр O окружности совпадает с серединой отрезка AD.
2. В случае, когда точка касания лежит на продолжении луча ВС за точку В (см. рис. 28), радиус окружности находится из прямоугольного треугольника GO1O , в
котором OO1G 60 , GO 4, GE1 1,
и равен GO1 GE1 8 1 7.
Ответ: 1 или 7.
Опорная задача. Отрезок общей внешней касательной к двум касающимся окружностям радиусов r и R равен
2
 Rr .
Rr .
R |
O2 |
O1 r |
R r |
|
E |
A B
Рис. 29
Доказательство. Из прямоугольного треугольника O1O2E (см. рис. 29) получаем
AB O1E 
 O1O22 EO22
O1O22 EO22

 (R r)2 (R r)2 2
(R r)2 (R r)2 2
 Rr .
Rr .
Пример 27. Окружности радиусов 4 и 9 касаются внешним образом, лежат по одну сторону от некоторой прямой и касаются этой прямой. Найдите радиус окружности, касающейся каждой из двух данных и той же прямой.
O1

 O2
O2

 E
E 

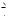

 O3 F
O3 F
M K P
Рис. 30а
Решение. Перебор вариантов в задаче зависит от расположения точки касания третьей окружности с прямой относительно точек касания первых двух окружностей с этой прямой. Рассмотрим первый случай касания искомой окруж-
18

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А.
ности с центром O3 , радиуса r3 и двух данных окружностей (см. рис. 30а). Тогда MP MK KP. Так как отрезок общей внешней касательной к двум касающимся
окружностям радиусов r и R равен 2 |
Rr |
||||||||||
(следует |
из |
|
ответа |
примера 16 |
при |
||||||
a R r |
или см. опорную задачу), |
то |
|||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
, |
|
|||
4 9 |
4 r3 |
9 r3 |
|
||||||||
откуда 6 2 |
|
3 |
|
|
или r3 1,44. |
|
|||||
r3 |
r3 |
|
|
||||||||
|
|
O3 |
O1 |
O2 |
F |
E |
||
M |
K |
P |
|
Рис. 30б |
|
Второй случай (см. рис. 30б) рассмотрите самостоятельно.
Ответ: 1,44 или 36.
Пример 28. Точка О – центр окружности радиуса 2. На продолжении радиуса ОМ взята точка А. Через точку А проведена прямая, касающаяся окружности в точке К. Известно, чтоOAK 60 . Найдите радиус окружности, вписанной в угол ОАК и касающейся данной окружности внешним образом.
Решение. Центр O1 искомой окружности лежит на биссектрисе угла А, поэтому O1 AK1 30 (рис. 31). K1 точка касания этой окружности с прямой АК.
|
|
O |
O |
|
M |
|
|
A |
K1 |
K |
K2 |
|
|
Рис. 31 |
|
Из |
треугольника O1AK1 |
находим |
|
AK1 r ctg30 r
 3, где r – радиус ис-
3, где r – радиус ис-
05.01.2011.
комой окружности. Из треугольника OAK находим
AK OK ctg60 2 .
 3
3
Рассмотрение случаев в данной задаче связано с расположением точки касания искомой окружности с прямой АK относительно точки касания K (левее, правее).
Отрезок внешней касательной окруж-
ностей с центрами О |
и O1 равен |
||||||||||||
2 |
OK O1K1 |
|
2 |
2r |
|
|
(см. опорную зада- |
||||||
чу). Тогда получаем |
|
|
|
|
|
||||||||
|
|
|
AK AK1 K1K , |
||||||||||
|
|
|
|
2 |
|
r |
|
2 |
|
. |
|||
|
|
|
|
|
3 |
2r |
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
||
Решаем квадратное уравнение
3t2 2
 6t 2 0,
6t 2 0,
где t 
 r . Получаем единственный по-
r . Получаем единственный по-
ложительный корень t |
|
2 |
3 6 |
. Тогда |
||||||||||
|
3 |
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
2 |
|
|
|
|
6 4 |
|
|
|
|
||||
3 |
6 |
2 |
|
|
|
|||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
||||||
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
Еще один случай расположения окружностей рассмотрите самостоятельно.
Ответ: 2 4 2 . 3
Пример 29. Найдите радиус окружности, вписанной в угол MKN равный 2arcsin0,6 и касающейся окружности, радиуса 4 также вписанной в угол MKN.
Решение. Центры окружностей вписанных в угол лежат на биссектрисе этого угла. Возможны два варианта расположения искомых окружностей (см. рис. 32). Пусть O центр данной окружности, O1 и O2 центры искомых с радиусами r и R соответственно. Тогда
OKN arcsin0,6.
1. Найдем радиус r. Проведем радиусы O1B1 и OB в точки касания со сторо-
ной KN и опустим из точки O1 перпен-
дикуляр O1C1 на OB . В прямоугольном
19
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. |
|
|
треугольнике |
O1OC1 |
OO1 4 r , |
OC1 4 r . Тогда из равенства
sin( OKN) OC1
O1O
получим уравнение
4 r sin(arcsin 0,6)
4 r
или
4 r 0,6.
4 r
Отсюда r 1.
M
|
|
O2 |
|
|
A2 |
|
|
|
O |
C2 |
|
O1 |
A1 |
||
|
|||
|
C1 |
|
|
K B1 |
B |
B2 N |
|
|
Рис. 32 |
|
2. При нахождении радиуса R , решая аналогичным образом, приходим к уравнению
R 4 0,6.
R 4
Откуда получаем R 16.
Ответ: 1 и 16.
05.01.2011.
4. Взаимное расположение элементов фигуры
В задачах этого типа фигурируют однотипные элементы фигуры (вершины, стороны, дуги, углы, высоты, биссектрисы, многоугольники и т.д.), однако условие допускает произвол выбора конкретного элемента из имеющихся у рассматриваемой фигуры.
выбор обозначений вершин многоугольника
К задачам этого типа относят такие задачи, условие которых допускает различные решения в зависимости от варианта буквенного обозначения вершин многоугольника.
Пример 30. В параллелограмме ABCD один из углов равен 60 . Точки E и F являются серединами смежных сторон, образующих острый угол. Площадь треугольника, отсекаемого прямой EF от параллелограмма ABCD, равна S . Найдите площадь треугольника, вершинами которого служат точки E, F и C .
● Медиана треугольника разбивает его на два равновеликих треугольника.Диагональ параллелограмма разбивает его на два равновеликих треугольника.
Решение. Используя приведенные выше
|
факты |
и построив |
||
E |
пунктиром два допол- |
|||
нительных отрезка (см. |
||||
|
||||
F |
рис. 33), получим, что |
|||
площадь |
параллело- |
|||
Рис. 33 |
грамма равна 8S . |
|||
|
Обозначение |
бук- |
||
вами вершин |
параллелограмма |
можно |
||
начать с любой вершины, поэтому возникает четыре разных рисунка, соответствующих условию данной задачи (см. рис. 34а, б, в, г). Треугольники, площадь которых нужно найти, на каждом из рисунков выделены темным фоном.
Площадь треугольника ECF на рис. 34а находим следующим образом:
SECF SABCD SAEF SEBC SFDC
11
8S S 2SABC 2SADC
20
