
matem-ege-shpora / математика С3
.pdf
http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
|
|
|
(2x 1) |
|
2 |
|
|
2x 1 3 9, |
|
|
|
log3 |
|
|
, |
|
|
|
|
||
3 |
1 |
|
||||||||
|
|
|
|
|
|
|
||||
|
log |
3 |
(2x 1) |
2 |
|
0 2x 1 |
9 |
. |
||
|
|
|
|
|
|
|
|
|
||
Отсюда получаем ответ.
Ответ: 1 x 4 , x 3 9 1. 2 9 2
9 1. 2 9 2
Пример 16. Решите неравенство
|2x x 2| 1 2x x 1.
Решение. Используя схему (22), получаем, что данное неравенство равносильно совокупности неравенств
На каждом из промежутков, на которые найденные точки разбивают ОДЗ, функции, стоящие под знаком модуля, имеют постоянный знак. Поэтому исходное неравенство на каждом промежутке заменяется на неравенство, не содержащее знаков абсолютной величины и равносильное исходному.
Пример 17. Решить неравенство
| x 1| | x 2| 3 x.
Решение. Решением совокупности
x 1 0,
являются числа 1 и 2.
x 2 0
|
x |
x 2| 1 2 |
x |
x 1, |
|2 |
|
|
||
|
|
x 2| 1 2x x 1. |
||
|2x |
||||
|
|
|
|
|
Используя схемы (20) и (22), получаем, что эта совокупность равносильна следующей.
2x x 2 2x x, |
|
||||||||
|
|
|
|
|
|
|
|
x, |
|
2x x 2 2x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
x 2 2 |
x |
|
|||||
2 |
|
|
x 2, |
||||||
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x 2 2 x 2 |
|||||||||
|
x 1, |
|
|
|
|
x 1, |
|||
|
|
x 1 |
2, |
|
|
|
|
|
|
|
2 |
|
|
|
x 0, |
||||
|
|
x 1 |
4, |
|
|
||||
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
x 1, |
||
|
x 0 |
|
|
|
|
x 0. |
|||
|
|
|
|
|
|
|
|
|
|
Ответ: ( ;0) (0;1) (1; ).
Для решения неравенств вида:
| f1(x)| | f2(x)| ... | fn(x)| g(x),
где символ заменяет один из знаков неравенств: , , , , применяют метод промежутков. Для этого находят ОДЗ неравенства, определяют точки разрыва функций f1(x), f2(x),..., fn (x) и находят корни совокупности уравнений
f1(x) 0,f2(x) 0,
...............
fn(x) 0.
Эти числа разбивают числовую прямую на три промежутка ( ;1) , [1; 2) и [2; ) . Освобождаясь от знаков модулей, с учетом знаков выражений под знаком модуля решим данное неравенство на каждом из этих промежутков (см. рис. 10).
x 1 |
|
|
|
|
|
x 2 |
|
1 |
|
|
2 x |
|
|
|
Рис. 10 |
|
|
Если |
x 1, |
то |
исходное |
неравенство |
|
равносильно неравенству |
|
|
|||
x 1 x 2 3 x |
x 0. |
||||
Получаем, что x 0 есть решение исходного неравенства на рассматриваемом промежутке.
Если 1 x 2, то исходное неравенство равносильно неравенству
x 1 x 2 3 x |
x 2. |
Следовательно, на этом промежутке решений нет.
Если x 2, то исходное неравенство равносильно неравенству
x 1 x 2 3 x |
x 6. |
Получаем, что x 6 есть решение исходного уравнения на рассматриваемом промежутке.
Объединяя полученные решения, запишем ответ.
Ответ: x 0, x 6.
21.01.2011. 11 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
расщепление неравенств |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Если левая часть неравенства представ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
4 0, |
(3) |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(II) |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
ляет собой произведение двух выражений, |
|
|
|
|
|
|
|
|
|
|
| x 3| 1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
(4) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
а правая часть равна нулю, то схема реше- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 x 1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
ния |
неравенства |
|
|
опирается |
на правило |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
Решим каждое неравенство системы (I). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
знаков при умножении (делении) положи- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Для неравенства (1) имеем: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тельных или отрицательных чисел. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 0, |
|
x |
3 |
4 0 |
|
|
|
|
|
(x 1)(x 3) |
0 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||
● |
|
f (x) g(x) 0 |
|
|
|
|
|
g(x) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x 1, |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(26) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для неравенства (2) имеем: |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 0, |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 3| 1 0 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
● |
|
f (x) g(x) 0 |
|
|
|
|
|
|
|
| x 3| 1 |
|
|
|
|
|
|
5 x 1 0, |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(27) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
| x 3| 1 0, |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 x 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 x 1 0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4, |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 3| 1, |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
g(x) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
● |
|
0 |
|
|
|
|
(28) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 x 1, |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) 0. |
|
|
|
|
|
|
|
|
|
|
|
|
| x 3| 1, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x 4, |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 x 1 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x 5 |
|
|||||||||||||||||||||||
|
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2. |
|
|
|
|||||||||||||||||
● |
|
0 |
|
|
|
|
g(x) 0, |
(29) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
g(x) |
|
|
|
f (x) 0, |
Значит все значения |
x (0;1] |
– решения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) 0. |
|
|
|
|
|
|
системы (I). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Пример 18. Решите неравенство |
|
Найдем решение системы (II). Для не- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
равенства (3), используя решение (1), име- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
x2 6x 9 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0, |
|
|
|
|||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ем: x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x 3.. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
5 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 0 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для неравенства (4), используя решение |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
6x 9 1 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
. |
(2) и учитывая ограничения |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
5 x 0, |
|
|
x 5, |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Решение. Приведем данное неравенст- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
во к следующему виду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 x 1 |
|
x 4 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
x |
2 |
|
6x 9 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x |
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|
| x 3| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x [2; 4) (4;5]. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 x 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
В соответствии со схемой полученное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Значит все значения |
x [2;3) |
– решения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
неравенство равносильно совокупности |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
систем (I) и (II): |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
системы (II). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Объединяя |
решения систем (I) |
и (II), |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
4 |
0, |
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
получаем ответ. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(I) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| x 3| 1 |
|
0; |
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (0;1] [2;3]. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
21.01.2011. 12 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
1.2. Метод замены
введение одной новой переменной
Пример 19. Решите неравенство
|
|
|
2 |
3. |
||
x |
||||||
|
|
|
||||
x 2 |
||||||
|
|
|
||||
Решение. Пусть 
 x t , где t 0. Тогда получаем рациональное неравенство
x t , где t 0. Тогда получаем рациональное неравенство
t |
2 |
3 |
|
(t 1)(t 4) |
0. |
|
t 2 |
||||
|
t 2 |
|
|
||
|
|
|
|
|
|
|
2 |
|
t |
Рис. 11
Решая последнее неравенство методом интервалов, получаем:
0 t 1, |
|
0 |
|
|
x 1, |
0 x 1, |
|||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|||||||||||
2 t 4 |
|
2 |
|
|
x 4 |
4 x 16. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Ответ: [0;1] (4;16]. |
|||||||
Пример 20. (МИОО, 2009). Решите не- |
|||||||||||||
равенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
6x2 5x |
6x2 5x 1 1 |
|||||||||||
Решение. Пусть |
|
|
|
|
|||||||||
|
|
6x2 5x 1 t, где |
|||||||||||
t 0, тогда получаем систему неравенств
|
1 |
|
|
1 |
|
, |
|
1 |
|
1 |
|
0, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
t 1 |
|
|
t 1 |
|||||||||
t2 |
|
|
|
t2 |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t 0 |
|
|
|
|
|
t 0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
t |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(t 1)(t 1) |
|
0 t 1. |
|||||||||||
|
|
|
|
||||||||||||
t 0
Выполняя обратную замену, получаем
|
2 |
5x 1 1, |
x(6x 5) 0, |
6x |
|
||
|
2 |
|
|
|
5x 1 0 |
(2x 1)(3x 1) 0. |
|
6x |
|
|
|
|
|
|
|
Отсюда получаем (см. рис. 12) 0 x 1 3
или 1 x 5 . 2 6
|
0 |
1 |
1 |
|
5 |
|
|
|
x |
|||||
|
|
3 |
2 |
|
6 |
|
|
|
|
|
|
|||
|
Рис. 12 |
|
|
|
|
|
|
|
|
|
|
|||
|
Ответ: 0 x |
1 |
или |
|
1 |
x |
5 |
. |
||||||
|
3 |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
6 |
|
|||||
Пример 21. (ЕГЭ 2010). Решите нера- |
||||||||||||||
венство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
log5 7 x2 |
5 7 x2 16 |
1 log5 |
7 |
x |
2 |
|
|
|
|
|
||||
|
|
5 |
|
|
||||||||||
|
2 |
16 1 |
||||||||||||
|
|
|
|
|
7 x |
|
|
|
||||||
|
|
|
log5 72 x2 |
1 2 . |
||||||||||
Решение. В соответствии с определением логарифма, входящие в неравенство выражения имеют смысл при выполнении условий:
7 x2 5 7 x2 16 1 0,
2 x2
7 1 0.
Сделаем замену 7 x2 t. Так как неравенство x2 0 выполняется при всех x, то по свойству степени с основанием боль-
ше единицы получаем 0 7 x2 |
70 |
1. |
Отсюда 0 t 1. С учетом последнего неравенства, запишем полученную выше систему
|
|
16 |
t 1 0, |
|
|
|
||
(t 5) 7 |
|
|
|
|
||||
|
2 t 1 0, |
0 t 7 16 . |
||||||
7 |
||||||||
0 t 1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Исходное неравенство с переменной t |
||||||||
будет иметь вид |
|
t 5 |
|
|
||||
log5 (t 5) 716 t 1 log5 |
|
|||||||
716 t 1 |
||||||||
|
|
|
|
|
|
|||
log5 (49t 1)2 |
, где 0 t 7 16 . |
|||||||
Используя свойство логарифма (при допустимых значениях переменной сумма логарифмов с одинаковым основанием равна логарифму произведения), получим
log5 (t 5)2 |
log5 72 t 1 2 |
|
(t 5)2 (49t 1)2 ,
21.01.2011. 13 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
так как (t 5)2 0 |
и (49t 1)2 0 при |
правее точки 2, сумма расстояний от точек |
|||
0 t 7 16 . Решим последнее неравенство: |
–2 и |
2 |
складывается |
из длины отрезка |
|
|
|
[ 2;2] |
и |
удвоенного |
расстояния от этой |
|
(t 5)2 |
(49t 1)2 |
|
|
|
(t 5)2 |
(49t 1)2 |
0 |
|
(t 5) (49t 1) (t 5) (49t 1) 0
(48t 4)(50t 6) 0 1 t 3 . 12 25
С учетом ограничения на t получаем
0 t 7 16 .
Выполнив обратную замену, имеем
7 x |
2 |
7 |
16 |
. Отсюда x2 16 |
|
x 4, |
. |
||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x 4. |
|
|
|
|
|
|
|
Ответ. ( ; 4) (4; ). |
|||||
|
Пример 22. (МФТИ, 2009). Решите не- |
||||||||||
равенство |
|
|
|
|
|
|
|
||||
|
logx 1 2 log2 |
x 1 |
|
|
|
|
|
||||
|
|
|
|
|
|||||||
4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|log2(4x 4) logx 1 2| 5.
Решение. Область определения данного неравенства определяется условиями
x 1 0, |
1 x 0, |
||||
|
|
|
|
||
x 1 1 |
|
|
x 0. |
|
|
Так как при допустимых значениях x |
|||||
справедливо равенство |
1 |
|
|||
logx 1 |
2 |
|
, |
||
log2 (x 1) |
|||||
|
|
|
|||
то, сделав замену log2 (x 1) t, получим неравенство
1 t 2 t 1 2 5. t t
Полагая t 1 u , получим неравенство t
|u 2| |u 2| 5.
Используем геометрический способ решения последнего неравенства (см. раздел «Геометрические методы решения»). Расстояние между точками –2 и 2 меньше 5, поэтому для каждой из точек отрезка [ 2;2] сумма расстояний до точек –2 и 2 меньше 5. Рассмотрим точки справа и слева от отрезка [ 2;2]. Для точки, лежащей
точки до точки 2. Искомые точки находятся правее точки 2 на расстоянии меньше (5 4):2 0,5. Аналогично искомые точки находятся слева от точки –2 на расстоянии меньше 0,5. Следовательно,
|u 2| |u 2| 5 2,5 u 2,5|u | 2,5.
Тогда |
t |
1 |
|
2,5 |
|
t2 |
1 |
2,5 |
|
|
|||||||||||||||||||||||
|
t |
|
|t | |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2|t |2 |
5|t | 2 0 |
|
|
0,5 |t | 2. |
|||||||||||||||||||||||||||||
Последнее неравенство равносильно |
|||||||||||||||||||||||||||||||||
совокупности двух неравенств |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
0,5 log2 (x 1) 2, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 log2 (x 1) 0,5 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
x 1 4, |
|
|
|
|
|
|
1 x 3, |
|||||||||||||||||||||||
2 |
|
|
2 |
||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|
1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
1. |
||||||||||||||
4 |
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||
Ответ. |
3 |
x |
|
1 |
|
|
1, |
|
|
1 x 3. |
|||||||||||||||||||||||
|
|
|
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
4 |
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
введение двух новых переменных
Пример 23. (Тренировочная работа МИОО, ЕГЭ 2011). Решите неравенство
x2 2x 1 |
|
x2 2x 1 |
|
|
(2x2 x 5)2 |
. |
||
(x 2)2 |
|
(x 3)2 |
|
2(x 2)2 (x 3)2 |
||||
|
|
|
||||||
Решение. Входящие в неравенство выражения имеют смысл при x 2 и x 3.
При всех остальных x неравенство равносильно следующему
2(x 3)2 (x 1)2 2(x 2)2 (x 1)2
(2x2 x 5)2 |
|
2(x2 4x 3)2 2(x2 3x 2)2 |
|
(2x2 x 5)2 . |
|
Заметим, что |
|
2x2 x 5 (x2 4x 3) (x2 3x 2) .
Пусть x2 4x 3 u и x2 3x 2 v. Тогда последнее неравенство примет вид
2u2 2v2 (u v)2 |
|
|
2u2 2v2 u2 2uv v2 |
|
|
21.01.2011. 14 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
u2 2uv v2 0 |
|
(u v)2 0. |
Отсюда следует, что u v. Выполняя обратную замену, получаем
x2 4x 3 x2 3x 2, т.е. x 1 . 7
Ответ. 1 . 7
тригонометрическая подстановка
Если область определения данного неравенства совпадает с областью значений тригонометрической функции, то иногда удобно использовать одну из замен:
x asint, |
t |
|
|
|
|
|||
|
|
; |
|
|
, |
|||
2 |
2 |
|||||||
|
|
|
|
|
|
|||
или
x acost , t 0; ,
для неравенств, содержащих выражения
a2 x2 ; |
|
|
|
|
|
|
|
x atgt, |
|
|
|
|
|
||
t |
|
|
; |
|
|
, |
|
2 |
|
||||||
|
|
|
|
2 |
|
||
или
x actgt, t 0; ,
для неравенств, содержащих выражения
a2 x2 ; |
|
|
|
|
|
|
|
|
|
|
| x | |
|
a |
, t |
|
0; |
|
, |
|||
|
|
|
|
|
|
|||||
|
sint |
|
|
|||||||
или |
|
|
|
|
|
2 |
|
|||
|
a |
|
|
|
|
|
|
|||
| x | |
|
, t |
|
|
|
|
||||
|
|
0; |
|
|
|
|
, |
|||
cost |
|
|
|
|||||||
|
|
|
|
|
2 |
|
||||
для неравенств, содержащих выражения 
 x2 a2 .
x2 a2 .
Пример 24. Решите неравенство
|
|
|
1 x2 4x3 3x . |
|
Решение. |
Для решения неравенства |
|
|
|
|
3x 0 используем метод |
1 x2 4x3 |
|||
интервалов. |
|
||
1.Пусть f (x) 
 1 x2 4x3 3x.
1 x2 4x3 3x.
2.D(f ) [ 1;1].
3.Найдем нули функции f (x), решив
уравнение 
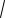 1 x2 4x3 3x 0.
1 x2 4x3 3x 0.
Так как уравнение определено при всех значениях x [ 1;1], то сделаем замену
|
|
|
|
|
|
|
|
|
||
x sint, |
t |
|
; |
|
|
. Уравнение примет |
||||
|
|
|||||||||
|
|
|
2 |
|
2 |
|
|
|
||
вид |
cost 4sin3 |
t 3sint |
0 |
или |
||||||
cost sin3t 0. Далее имеем |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
t |
sin3t 0 |
|
|
||||
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2sin |
|
|
t cos |
2t |
|
|
0 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||||||||||
sin |
|
|
t 0, |
|
|
|
|
|
n, |
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||
cos 2t |
|
0, |
|
t |
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||||
|
|
8 |
|
|
2 |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где n,k Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Поскольку промежутку |
|
|
|
|
; |
|
|
|
|
|
при- |
|||||||||||||||||
|
2 |
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
надлежат три числа |
|
|
|
, |
|
|
|
|
|
и |
|
3 |
, |
то |
||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
8 |
|
|
|
|
|
|
|
8 |
|
|
|||||
корнями рассматриваемого уравнения яв-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ляются |
числа |
sin |
|
|
|
, |
|
sin |
|
, и |
|||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
8 |
|||||||
sin |
3 |
. Так как |
|
|
|
|
|
3 |
, |
то в силу |
|||||||||||||||
8 |
|
|
|
|
|
|
|
4 |
|
|
8 |
|
8 |
|
|
|
|
|
|||||||
возрастания функции |
|
y sint |
на проме- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
жутке |
|
; |
|
|
|
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||
|
|
sin |
|
|
|
|
|
sin |
|
|
|
|
|
|
sin |
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|||||||
4. Найдем промежутки знакопостоянства функции f (x).
Так как f (x) непрерывна, как сумма непрерывных функций, и f (0) 0, то по-
лучаем, что |
f (x) 0 при всех значениях |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x 1; |
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
; sin |
|
|
|
|
|
. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
8 |
8 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Ответ: 1; |
|
|
|
|
|
|
|
|
sin |
|
|
; sin |
|
. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
8 |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|||||||||||||||
Замечание. |
|
|
|
|
|
|
Если |
|
|
|
|
|
учесть, |
|
|
|
|
что |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
, sin |
3 |
|
|
|
|
|
|
2 |
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||
sin |
|
2 |
|
|
|
|
|
2 |
то от- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вет можно записать в следующем виде: |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||
|
1; |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
21.01.2011. 15 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
1.3. Разбиение области определения |
|
(x 2)(x 2) 0. |
неравенства на подмножества |
Отсюда |
получаем два промежутка: |
|
Разбиение ОДЗ неизвестной неравенства на промежутки позволяет упростить некоторые неравенства. Решение неравенства рассматривают отдельно на каждом промежутке.
Пример 25. Решите неравенство
2x 2 x 2
 2.
2.
Решение. Данное неравенство определено при всех значениях х. Рассмотрим два случая.
1. Пусть x 0, тогда неравенство примет следующий вид:
2x 2x 2 |
|
2x |
|
x |
1 |
(в силу |
|
2 |
2 |
||||||
|
|||||||
|
|
|
2 |
|
|||
возрастания функции y |
2t ). |
|
|||||
2. Если x 0, то имеем:
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 t 1 0, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|||||
|
x |
|
1 |
|
|
|
|
|
|
|
x |
t, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
2 2 2 |
|
|
|
|
|
||||||
|
|
2x |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
1, |
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 1, |
|||||||
|
|
t |
2 1, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
x |
|
t, |
|
|
2x |
2 1, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||||
x log2 (
 2 1),
2 1),
x log2 (
 2 1).
2 1).
С учетом условия x 0 получаем, что x log2 (
 2 1) является решением неравенства на рассматриваемом промежутке,
2 1) является решением неравенства на рассматриваемом промежутке,
поскольку log2(
 2 1) log2 1 0, а
2 1) log2 1 0, а
log2(
 2 1) log2 2 1.
2 1) log2 2 1.
Объединим решения, полученные в
первом и втором случаях. |
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|||
Ответ: ;log2 ( |
2 1) |
|||||||
|
|
; . |
||||||
|
||||||||
|
|
|
|
|
2 |
|
||
Пример 26. Решите неравенство |
|
|||||||
log2 x2 4 3log2 |
|
x 2 |
2. |
|
||||
|
|
|
||||||
|
|
x 2 |
|
|
|
|||
Решение. Область определения данного неравенства определяется условием:
( ; 2) и (2; ).
Рассмотрим два случая. 1. Пусть x 2.
Тогда неравенство примет следующий вид:
log2 (x 2) log2 (x 2) 3log2 (x 2)3log2(x 2) 2
или
2log2 (x 2) log2 (x 2) 1.
Отсюда
(x 2)2 2(x 2) или x(x 6) 0.
Сучетом условия x 2 получаем x 6.
2.Пусть x 2. В этом случае неравенство примет следующий вид:
log2 (2 x) log2 ( x 2) 3log2 ( x 2)3log2 (2 x) 2
или
2log2 (2 x) log2 ( x 2) 1.
Отсюда
(2 x)2 2( x 2) или x2 2x 8 0.
Так как уравнение x2 2x 8 0 не имеет корней и старший коэффициент положителен, то последнее неравенство выполняется при всех действительных зна-
чениях x, |
т.е. на всем рассматриваемом |
||||||
промежутке. |
|
|
|
|
|
||
В этом случае все значения |
x 2 яв- |
||||||
ляются решениями неравенства. |
|
||||||
Объединим полученные решения. |
|||||||
|
|
|
Ответ: x 2 |
или x 6. |
|||
Пример 27. Решите неравенство |
|||||||
1 |
x2 |
2x 15 3/2 |
(x 3)2 |
|
|
|
|
|
7 |
(x 5) |
1. |
||||
|
|
|
|
|
|||
|
|
|
|||||
2 |
|
|
|
|
|
||
Решение. ОДЗ неизвестной данного не- |
|||||||
равенства |
|
находим |
из |
|
условия |
||
x2 2x 15 0, т.е. x 3 или x 5. Рассмотрим исходное неравенство на
двух промежутках: 1) x 3 и 2) x 5. 1. При x 3 исходное неравенство
равносильно неравенству
21.01.2011. 16 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
|
|
7x2 2x 15 x 3 |
|
|
1 |
|
||||||
|
|
|
|
|
|
|
||||||
|
|
2x2 2x 15 x2 2x 15 |
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
1. |
|
2x2 2x 15 |
|
|
|
7x2 |
|
|
||||||
x2 |
|
|
|
|||||||||
|
2x 15 |
|
x 3 |
|||||||||
|
|
|
|
2x 15 |
||||||||
Поскольку при |
x 3 верно каждое из |
|||||||||||
|
|
|
|
|
|
|||||||
неравенств: x 3 0, |
|
|
|
x2 2x 15 0, |
||||||||
7x2 2x 15 1, 2x2 2x 15 1, то в этом случае левая часть неравенства меньше либо равна 1 для любого значения x из этого промежутка.
2. Пусть x 5. Заметим, что неравенст-
во x 3 
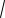 x2 2x 15 справедливо на всем этом промежутке. Это следует из его решения
x2 2x 15 справедливо на всем этом промежутке. Это следует из его решения
x 3 
 x2 2x 15
x2 2x 15
x2 6x 9 x2 2x 15 x 3.
a t
В силу возрастания функции y ,
b
где |
|
a b 0, |
t |
0, |
из неравенства |
||||
a |
t |
|
|
t |
|
t |
|||
|
|
|
|
1 следует a |
|
b |
. Поэтому имеем |
||
|
|
||||||||
b |
|
|
|
|
|
|
|||
|
|
7x2 2x 15 2x2 |
2x 15 |
1, причем равен- |
|||||
ство достигается при |
x 5 на рассматри- |
||||||||
ваемом промежутке, при всех x 5 справедливо строгое неравенство.
Отсюда получаем
7x2 2x 15 x 3 |
2x2 2x 15 x 3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2x2 2x 15 |
|
. |
|
|
|
|
|
|
|
|
|
x2 2x 15 |
|||||
Тогда |
7x2 2x 15 x 3 |
|
|
1 при x 5 |
|||||||||
|
|
|
|
|
|
||||||||
|
|
2x2 2x 15 x2 2x 15 |
|
|
|
||||||||
и |
7x2 2x 15 x 3 |
|
|
|
1 |
при x 5. |
|||||||
|
|
|
|
|
|||||||||
|
2x2 2x 15 x2 2x 15 |
|
|
|
|
|
|
||||||
|
Значит исходное неравенство на рас- |
||||||||||||
сматриваемом |
промежутке выполняется |
||||||||||||
только при x 5.
Объединим решения, полученные в первом и втором случаях.
Ответ. x 3 и x 5.
2. Функционально-графические методы решения
Область применения свойств функции при решении неравенств очень широка. Наличие свойств (ограниченность, монотонность и т.д.) функций, входящих в неравенства позволяет применить нестандартные методы решения к стандартным по формулировке задачам – неравенствам.
Начнем с примера, связанного с композицией функций.
Пример |
28. |
|
(МИЭТ, |
2002). |
Пусть |
||||||||||||||||||||||||||||||||||||
f (x) |
|
x2 14x 33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
g(x) |
|
x . |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
Решите |
|||||||||||||||||||||||
|
|
|
9 x2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
неравенство f g(x 9) f (4). |
|
|
|
||||||||||||||||||||||||||||||||||||||
Решение. Так как,g(x 9) |
|
|
|
|
|
|
|
, то |
|||||||||||||||||||||||||||||||||
|
|
|
|
x 9 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
f g(x 9) f ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
x 9) |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
( |
|
|
|
|
|
|
14 |
|
|
|
|
|
33 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
x 9)2 |
x 9 |
. |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
9 ( |
x 9)2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
f (4) |
42 |
14 4 33 |
|
|
|
||||||||||||||||||||||||||||
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, то не- |
||||||||||||||||||
|
|
|
|
|
|
9 42 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
равенство |
f g(x 9) f (4) |
примет вид |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
x 9)2 14 x 9 33 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
9 ( |
|
|
|
x 9)2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Сделав замену t |
|
|
|
|
, где t |
|
0, по- |
||||||||||||||||||||||||||||||||||
|
|
|
x 9 |
|
|||||||||||||||||||||||||||||||||||||
лучим систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
14t 33 |
|
|
|
|
|
|
|
|
2 |
7t 12 |
|
|
|
|
|
||||||||||||||||||||||||
|
t |
|
1, |
|
|
|
|
t |
|
|
|
0, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
9 t2 |
|
|
|
|
|
|
|
9 t2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
(t 3)(t 4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 4 |
0, |
||||||||||||||||||||||
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
(t 3)(t 3) |
|
|
|
|
|
|
|
t |
3 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 t 3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 t 4. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Возвращаясь к переменной x, получим |
|||||||||||||||||||||||||||||||||||||||||
0 |
|
3, |
|
|
|
|
|
|
|
|
0 x 9 9, |
||||||||||||||||||||||||||||||
x 9 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x 9 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
9 x 9 16 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 x 18, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
18 x 25. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ответ: 9 x 18, 18 x 25.
21.01.2011. 17 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
2.1. Использование области определения функции
Предварительный анализ области допустимых значений неизвестной неравенства иногда позволяет получить решения без преобразований неравенства.
Пример 29. (МИЭТ, 1998). Решите не-
равенство

 x2 3x 2 x3 9.
x2 3x 2 x3 9.
Решение. Область определения неравенства задается условием:
x2 3x 2 0 |
1 x 2. |
Для этих значений x получаем:
1 x 2 |
1 x3 8 |
|
8 x3 9 1,
т.е. правая часть исходного неравенства отрицательна на его области определения. Следовательно, неравенство справедливо при всех 1 x 2.
Ответ: 1 x 2.
Пример 30. Решите неравенство

 x2 6x 5 1 log5 x 5
x2 6x 5 1 log5 x 5
1 
 12x 2x2 10 1 0. x
12x 2x2 10 1 0. x
Решение. Область определения неравенства задается условиями:
|
|
x2 6x 5 0, |
|
|
x 1, |
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
12x 2x2 10 0, |
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
x 0 |
|
|
|
x 5. |
||||
|
|
|
|
|
|
|
|
|
||
|
|
Подставляя |
полученные |
значения в |
||||||
данное неравенство, получим: |
|
|||||||||
|
|
при |
x 1 |
что исходное |
неравенство |
|||||
примет вид |
|
|
|
|
||||||
|
|
log |
|
1 |
1 0 или |
0 0, т.е. будет не- |
||||
5 |
5 |
|||||||||
|
|
|
|
|
|
|
|
|||
верно; |
|
|
|
|
|
|
||||
|
1 |
при |
x 5 |
имеем |
верное |
неравенство |
||||
|
0. |
|
|
|
|
|
|
|||
5 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
Ответ: 5.
2.2. Использование непрерывности функции
Сформулируем свойство непрерывных функций: если функция f (x) непрерывна на интервале и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.
На этом свойстве основан метод решения неравенств с одной переменной – метод интервалов. Обобщения метода интервалов связаны с расширением класса функций, входящих в неравенство.
В основе метода интервалов лежат следующие положения:
1.Знак произведения (частного) однозначно определяется знаками сомножителей (делимого и делителя).
2.Знак произведения не изменится (изменится на противоположный), если изменить знак у четного (нечетного) числа сомножителей.
3.Знак многочлена справа от большего (или единственного) корня совпадает со знаком его старшего коэффициента. В случае отсутствия корней знак многочлена совпадает со знаком его старшего коэффициента на всей области определения.
4.Пусть на промежутке (a;b) задана
возрастающая |
(убывающая) функция |
f (x), причем |
x0 – корень уравнения |
f (x) 0, принадлежащий промежутку (a;b). Тогда функция f (x)справа от корня положительна (отрицательна), слева отрицательна (положительна), т.е. при переходе через корень меняет знак.
метод интервалов
Сформулируем свойство чередования знака линейного двучлена ax b (a 0):
при переходе через значение x0 |
|
b |
знак |
|
a |
||||
|
|
|
выражения ax b меняется на противоположный. Знание свойства чередования знака линейного двучлена ax b позволяет в дальнейшем не приводить линейные двучлены к каноническому виду x x0 .
Свойство двучлена ax b лежит в основе метода интервалов и часто исполь-
21.01.2011. 18 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
зуется при решении алгебраических неравенств более высоких степеней.
Рассмотрим функцию
|
f (x) |
f1(x) f2 (x) ... fn (x ), |
(*) |
|||
где |
fi (x) ai x bi , |
причем |
выражения |
|||
ai x bi |
и |
aj x bj |
попарно различны |
|||
(ai |
0 |
и |
aj |
0, |
i 1, 2,..., n; |
|
j 1, 2,..., n; |
i j). |
Выражению (*) соот- |
||||
ветствует разбиение числовой прямой на
интервалы точками xi |
|
bi |
(i 1, 2,..., n). |
|
ai |
||||
|
|
|
Метод интервалов опирается на следующее свойство чередования знака функции
(*): при переходе через точку xi |
|
bi |
из |
|
ai |
||||
|
|
|
одного интервала в смежный знак значения функции (*) меняется на противоположный.
Действительно, при переходе через точ-
ку x bi в выражении (*) меняет знак ai
только один множитель ai x bi .
Пример 31. Решите неравенство
(2x2 5x 3)(3 3 x) 0.
3 x) 0.
Решение. Перепишем неравенство в следующем виде
(2x 3)(x 1)(3
 3 x) 0,
3 x) 0,
и далее используем метод интервалов. 1. Обозначим
f(x) (2x 3)(x 1)(3 3 x).
3 x).
2.D(f ) R.
3.f(x) 0; (2x 3)(x 1)(3
 3 x) 0.
3 x) 0.
Отсюда получаем корни уравнения: 1;
1,5; |
3 3. Так |
как 1 3 1,53 3,375, то |
|
1 3 |
|
1,5. |
|
3 |
|
||
4. Найдем промежутки знакопостоянства |
|||
функции f (x). |
Так как f (0) 0, то рас- |
||
ставляем знаки в соответствии с правилом знакочередования, как показано на рис. 13.
|
|
|
|
|
1 |
3 3 1,5 |
x |
|
|
Рис. 13 |
|
Получаем все значения
x (1;3 3) (1,5; ),
3) (1,5; ),
при которых f (x) 0.
|
|
Ответ: |
(1;3 |
3) (1,5; ). |
||||||||||
|
|
|
f(x) |
0 |
|
|
|
|
|
f (x) |
|
|||
Неравенство |
|
|
|
|
или |
|
|
|
|
0 |
||||
|
|
|
|
|
|
|
||||||||
|
|
|
g(x) |
|
|
|
|
|
|
g(x) |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
равносильно неравенству |
|
|
f(x)g(x) 0 |
|||||||||||
(соответственно |
|
f (x)g(x) 0). Нестрогое |
||||||||||||
|
f(x) |
0 |
|
|
|
|
|
f (x) |
|
|||||
неравенство |
|
|
|
|
или |
|
|
|
|
0 |
||||
|
|
|
|
|
|
|
||||||||
|
g(x) |
|
|
|
|
|
|
|
g(x) |
|
||||
|
|
|
|
|
|
|
|
|
||||||
равносильно |
|
системе |
|
|
f(x)g(x) 0 |
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
g(x) 0 |
|
|||||
|
|
f (x)g(x) 0 |
|
|
||||||||||
соответсвенно |
|
|
|
|
|
|
|
|
. |
|
||||
|
|
g(x) 0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
На практике неравенство |
|
f(x) |
0 |
ре- |
||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
g(x) |
|
||||
шают, не приводя его к виду f(x)g(x) 0, где символ заменяет один из знаков неравенств: , , , .
Рассмотрим неравенство f(x) 0, где g(x)
f(x) и g(x) – функции вида (*).
Пример 32. Решите неравенство
x2 2x 3 3. x2 4x 3
Решение. Приведем неравенство к виду
(2x 3)(x 2) 0 (x 1)(x 3)
ииспользуем метод интервалов.
1.Пусть f (x) (2x 3)(x 2) . (x 1)(x 3)
2.D( f ) ( ;1) (1;3) (3; ).
3.Нули функции f (x) найдем из уравнения (2x 3)(x 2) 0. Корни последнего уравнения 1,5 и 2 принадлежат D(f ).
4.На каждом из промежутков ( ;1),
(1;1,5), (1,5;2), (2;3) , (3; ) функция f (x) непрерывна и сохраняет постоянный знак. Так как f (0) 0, то на промежутке ( ;1) функция f (x) 0. На остальных
21.01.2011. 19 www.alexlarin.narod.ru

http://vk.com/ege100ballov
Корянов А.Г., Прокофьев А.А. Методы решения неравенств с одной переменной.
промежутках расставляем знаки по правилу знакочередования (см. рис. 14).
|
|
|
|
|
|
|
|
2 |
|
x |
|
|
|
Рис. 14 |
|
|
|
Следовательно, f (x) 0 при всех зна-
чениях x ( ;1) (1,5;2) (3; ).
Ответ: ( ;1) (1,5; 2) (3; ).
первое обобщение метода интервалов
Пусть дана функция вида
f (x) |
f1k1 (x) f2k2 |
(x) ... fnkn (x), (**) |
|
где fi (x) ai x bi , |
причем |
выражения |
|
ai x bi и |
aj x bj |
попарно |
различны |
Сравним полученные числа. Так как
7 9, то 
 7
7 
 9 и
9 и 
 7 3.
7 3.
Аналогично из неравенства 7 2,642
6,9696 получаем 
 7
7 
 2,642 и
2,642 и

 7 2,64.
7 2,64.
4. Найдем промежутки знакопостоянства функции f (x) 0. Так как f (0) 0, то далее расставляем знаки левой части исходного неравенства, учитывая кратность корней, как показано на рис. 15.
2,64 |
|
|
x |
Рис. 15
Отсюда f (x) 0 при всех значениях x [2,64;
 7] 3 .
7] 3 .
(ai 0 |
и |
aj 0, |
i 1, 2,..., n; |
j 1, 2,..., n; |
i j)., k1, k2 ,..., kn – фик- |
||
сированные натуральные числа.
Для решения неравенства f (x) 0, где выражение f (x) имеет вид (**), использу-
ется обобщенный метод интервалов, ко-
торый опирается на следующее правило чередования знаков выражения: при пере-
ходе через точку xi |
|
bi |
из одного ин- |
|
ai |
||||
|
|
|
тервала в смежный знак значения функции (*) меняется на противоположный,
если ki – нечетное число, и не меняется,
если ki – четное число.
Пример 33. Решите неравенство
|
2 |
|
|
|
16 |
|
|
|
|
|
|
||||
(x 3) |
|
(x |
7) x 2 |
|
|
0. |
|
|
25 |
||||||
|
|
|
|
|
|
|
|
Решение. 1. Рассмотрим функцию
Ответ: [2,64;
 7] 3 .
7] 3 .
второе обобщение метода интервалов
Применимость метода интервалов не ограничивается решением рациональных неравенств.
Метод интервалов допускает обобщение на выражения вида
f1k1 (x) f2k2 (x) ... fnkn (x),
где fi (x) функции, непрерывные на сво-
ей области определения (i 1, 2,..., n;
k1, k2 ,..., kn – фиксированные натураль-
ные числа).
Пример 34. Решите неравенство
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
32 |
x |
4 |
|
|
|
(2x 5) |
|
|
|
|||
|
|
|
|
|
0. |
|
(3x 8)(x4 |
4x 20) |
|||||
|
||||||
Решение. Так как при x 1 многочлен
|
|
|
|
2 |
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f (x) (x |
3) |
|
(x |
|
7) x 2 |
|
. |
||||||
|
|
|
25 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
D(f ) R. |
|
|
|
|
|
|
|
f(x) из урав- |
|||||
3. |
Найдем нули функции |
|||||||||||||
|
|
2 |
|
|
|
|
|
|
16 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
нения (x 3) |
|
(x |
|
7) x 2 |
|
|
0. От- |
|||||||
|
|
25 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
сюда x 3 или x 
 7 , или x 2,64.
7 , или x 2,64.
x4 4x 20 принимает наименьшее значение 17 (докажите с помощью производной), то неравенство x4 4x 20 0 выполняется при всех значениях х. Тогда данное неравенство принимает вид
|
|
1 |
|
|
||
32x |
4 |
|||||
(2x 5) |
|
|||||
|
|
|
|
|
||
|
|
|
|
|
0. |
|
3x |
8 |
|
|
|||
|
|
|
||||
21.01.2011. 20 www.alexlarin.narod.ru
