1.3. Закон Ома

а) Участок цепи содержит только резистор R

Между током, напряжением и сопротивлением участка цепи существует, как было записано (1.1),

зависимость

Это и есть закон Ома. Размерность: U –в вольтах, В, I - в амперах, А; R – в омах, Ом. Наряду

с сопротивлением R при расчетах вводят понятие проводимости участка цепи как

величину, обратную сопротивлению

g =

При этом g - в сименсах, См = Ом^-1.

Перепишем закон Ома в таком виде

Если сопротивление (проводимость) элемента цепи не зависит от тока в нём, то график I(U), т. е. вольт - амперная характеристика (ВАХ) элемента, представляется в виде прямой линии (см. рис. 1.6). В этом случае говорят, что элемент цепи обладает линейной характеристикой. В первой части курса мы будем заниматься только линейными цепями.

б) Участок цепи содержит источники ЭДС

Если на участке цепи есть одна или несколько ЭДС, то для того чтобы записать закон Ома, рассмотрим изменение потенциала вдоль такого участка (рис. 1.7).

Пусть известен потенциал точки 2. Проследим изменение потенциала при переходе от точки 2 к точке 1 в соответствии с правилами, изложенными в параграфе 1.2

Пусть известен потенциал точки 2. Проследим изменение потенциала при переходе от точки 2 к точке 1 в соответствии с правилами, изложенными в параграфе 1.2

; ; ;

; или

;

;

.

Из последнего выражения определим ток

(1.3)

Анализируя полученную формулу, следует отметить, что значение тока по (1.3) может иметь как положительный, так и отрицательный знак. На это обратим особое внимание.

При расчёте цепей направления токов, как правило, заранее не известны. Поэтому перед началом расчёта их направления выбирают произвольно. Такие направления токов называют положительными. Если при расчёте получается ток с отрицательным знаком, то это значит, что положительное направление тока прямо противоположно действительному. То же самое относится и к выбору положительных направлений напряжений.

1.4. Эквивалентные схемы источников энергии

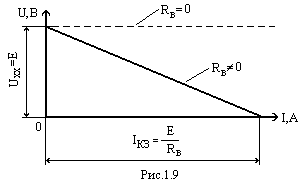
Реальный источник электрической энергии имеет внешнюю характеристику, представленную на рис. 1.9, и может быть представлен в виде двух эквивалентных схем.

а) Схема с источником ЭДС. Источник напряжения

Рассмотрим схему, в которой внутреннее сопротивление источника R_b условно изображено отдельно (рис. 1.8).

Ток в данной схеме (1.4) Напряжение на зажимах нагрузки (1.5) Из двух последних уравнений можно получить (1.6) (1.7)

Уравнение (1.7) при Е = const и R_В = const есть уравнение прямой линии (рис. 1.9). В то же время оно является ВАХ левой части схемы рис. 1.8, т. е. внeшней характеристикой источника напряжения U= f (I) (см. рис. 1.9)

Для её построения рассмотрим два режима.

Режим холостого хода (Х.Х); R_Н = ; (рис. 1.10).

Из (1.7) при I = 0 имеем

U = U_XX = E (1.8)

Режим короткого замыкания (КЗ); R_Н = 0; (рис. 1.11).

Из (1.7) при U = 0

(1.9)

По этим двум режимам можно построить ВАХ (внешнюю характеристику) источника напряжения (см. рис. 1.9), или по известной характеристике определить параметры E и RВ источника. Если внутреннее сопротивление источника RВ равно нулю, то получается идеальный источник, и по (1.7) при Rв = 0 U = E Внешняя характеристика U = f (I) такого источника показана на рис. 1.9 (пунктир).

В этом случае имеем идеальный источник напряжения с ЭДС E = const. Реальный источник напряжения приближается к идеальному, если он работает в режиме, близком к режиму холостого хода (1.8).Предыдущую схему можно представить другой эквивалентной схемой (относительно нагрузки).

Из (1.7) получаем

10 (1.)

Обозначая согласно (1.9) ; и далее , имеем , или , (1.11) где J – ток источника тока. Выражению (1.11) соответствует схема (см. рис.1.12).

Из уравнения (1.10) (1.12)

Это есть внешняя характеристика источника энергии I = f(U), изображенного на рис.1.13. Это схема с источником тока J.

Режим холостого хода. R_Н = ; I = 0; (рис. 1.14). Из (1.12)

Режим короткого замыкания. R_Н = 0; (рис. 1.15).

Из (1.12)

По данным этих двух режимов можно построить внешнюю характеристику источника I = f(U).

Если внутреннее сопротивление источника велико (R_В  ; g_В  0), то получается идеальный источник и по (1.12) при R_В   оказывается, что J = I. Говорят, что в этом случае имеем идеальный источник тока J = const (см. рис. 1.16). Внешняя характеристика I = f(U) такого источника показана на рис 1.13 пунктиром. Реальный источник электрической энергии с источником тока приближается по своим свойствам к идеальному, если он работает в режиме, близком к режиму короткого замыкания. Внутреннее сопротивление источника тока бесконечно велико.

Примерами источников напряжения, приближающимися к источнику ЭДС, могут быть различные генераторы постоянного тока с регулируемым напряжением на выходных зажимах. В качестве примера источника тока, приближающемуся к идеальному, могут быть названы, например, источники энергии основанные на излучении заряженных частиц, так как при этом ток источника определяется скоростью распада. Другими примерами могут служить генераторы постоянного тока с регулируемым током на выходе.

При расчетах электрических цепей реальный источник электрической энергии представляют источником напряжения или источником тока, в том числе и в случаях, когда за внутреннее сопротивление источника принимается любое сопротивление, соизмеримое с сопротивлением нагрузки. Переход от одной схемы к другой иногда значительно облегчает расчеты.

Рассмотрим правила перехода от одного вида источника к другому

Пример 1.1. На рис.1.17.приведена схема с источником ЭДС Е=12 В; R_B=2 Ома. Необходимо

перейти к схеме с источником тока.