1.2. Электрическое напряжение. Электрический потенциал. Разность потенциалов. Изменение потенциала вдоль участка цепи

Рассмотрим область пространства, в котором существует электрическое поле. Это может быть поле неподвижных зарядов или поле постоянных токов, протекающих по неподвижным проводникам, при условии, что поле исследуется вне области действия источников электродвижущих сил.

При перемещении какого-либо заряда из одной точки в другую силы поля, действующие на заряд, совершают работу. Отношение этой работы к переносимому заряду называется электрическим напряжением между рассматриваемыми точками.

Иногда вместо термина «напряжение между точками» употребляют термин «падение напряжения между точками».Если конечная точка для всех перемещений рассматриваемого пространства задана, то величина совершаемой работы при перемещении заряда из произвольной точки А в конечную точку N будет функцией только координат точки А. Отношение величины работы к величине заряда называют потенциалом точки А.

Следует отметить: что путь перемещения заряда может проходить в средах, различающихся друг от друга своими свойствами (например, в диэлектриках, в проводниках и т. д.).

Величина работы, совершаемой силами поля, определяется только положением начальной и конечной точек пути перемещения заряда. В соответствии со сказанным можно определить напряжение между точками А и В как разность потенциалов между этими точками:

Потенциал заданной конечной точки можно считать равным нулю.

Под воздействием электрического поля, созданного источниками электрической энергии внутри проводников, в них начинается упорядоченное движение зарядов – электрический ток.

Проследим изменение потенциала вдоль участка электрической цепи. Это позволит установить общие правила, которыми мы будем пользоваться в дальнейшем.

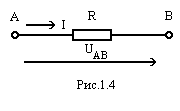
Рассмотрим участок электрической цепи, содержащий только резистор R, по которому протекает ток I (рис. 1.4). Ток протекает от точки А с более высоким потенциалом к точке В с более низким потенциалом. Пусть известен потенциал точки А. Определим потенциал точки В.

Пусть известен потенциал точки А. Определим потенциал точки В. Он будет меньше потенциа

ла точки А на величину падения напряжения на резисторе R:

Разность потенциалов между точками А и В – есть напряжение между этими точками

(1.1)

Если же известен потенциал точки В, то потенциал точки А при заданном направлении тока

будет выше потенциала точки В на величину падения напряжения на резисторе R:

и напряжение определяется аналогично предыдущем

Очевидно, что (см. рис. 1.4).

Рассмотрим участок цепи, содержащий только ЭДС Е (см. рис. 1.5). Пусть известен потенциал точки А. При переходе через источник ЭДС (по стрелке) потенциал повышается на величину ЭДС Е. Поэтому для потенциала точки В следует записать и разность потенциалов

Если же известен потенциал точки В, то потенциал точки A меньше на величину ЭДС Е

(переход через источник осуществляется против стрелки).

Разность потенциалов получается такой же

Очевидно, что (см. рис. 1.5).