Решение

/_m = 1,0 A;  = 120°; следовательно . Строим вектор на комплексной плоскости (рис. 4.9).

Пример 4.2. Дано: комплексная амплитуда тока 3аписать выражение мгновенного значения это по тока.

Решение

Для перехода от комплексной амплитуды к мгновенному значению надо умножить наи взять мнимую часть от полученного произведения

Под комплексом действующего значения тока, или под комплексом тока (комплексным

током), понимают частное от деления комплексной амплитуды на:

Пример 4.3. Дано:

Записать выражение комплекса действующего значения тока и построить его на комплексной плоскости.

Решение

Строим вектор на комплексной плоскости (рис. 4.9).

4.6. Действия с комплексными числами. Векторная диаграмма

Д е й с т в и я с к о м п л е к с н ы м и ч и с л а м и л е г ч е о с в о и т ь н а п р и м е р а х.

Сложение и вычитание комплексных чисел

Пусть даны комплексные числа . Найдем их сумму

Найдём их разность

В н и м a н и е! Сложение и вычитание комплексных чисел удобнее выполнять, представляя комплексы в алгебраической форме записи.

Умножение и деление комплексных чисел

Пусть даны два комплексных числа:

В н и м а н и е! Для умножения и деления комплексных чисел лучше представить их в показательной форме

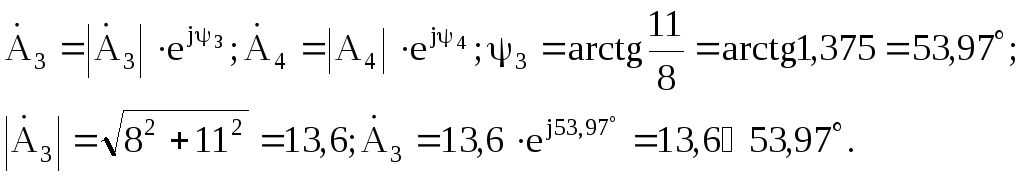
В н и м а н и е! При переводе комплексного числа из алгебраической формы в показательную с помощью калькулятора или ЭВМ необходимо, чтобы вещественная часть числа была положительной. Например,

и можно оперировать далее комплексом записанном в таком виде.

Но можно учесть, что

Тогда

Предпочтительнее взять комплекс с меньшим аргументом

Произведение двух комплексных чисел

Пусть даны два числа:

Произведение двух комплексных чисел

Пусть даны два комплексных числа

Частное от деления двух чисел

В н и м а н и е! При делении двух комплексных чисел они должны быть представлены в показательной форме

Возведение в степень комплексного числа

Пусть дано число: . ;

и т.д.

Логарифмирование

Пусть

где k = 0, 1, 2, 3 ...

При k = 0 получили главное значение.

Извлечение корня

Пусть дано число ;

где k = 0, 1, 2 ...

При k = 0 получили главное значение.

Проиллюстрируем удобство применения комплексного метода на примере.

Пример 4.4. Дано

Определить сумму i₁ + i₂ = i с помощью сложения векторов на комплексной плоскости.

Р е ш е н и е

Получили в алгебраической форме записи.

Построим на комплексной плоскости (рис. 4.10) по имеющимся координатам: действительная часть 3,59; мнимая часть – 1,03;

Запишем в показательной форме

Перейдем к мгновенному значению

Векторы показаны на рис. 4.10.

Геометрическая сумма векторов идает комплексную амплитуду суммарного токаАмплитуда тока определяется длиной (модулем) суммарного вектора, а начальная фаза – углом, образованным этим вектором и осью +1.

Обратим внимание на то, что если бы векторы ,изображенные на рис. 4.10, стали вращаться вокруг начала координат с угловой скоростью, то взаимное расположение векторов по отношению друг к другу осталось бы без изменений.

На рис. 4.10 дан пример векторной диаграммы. Векторной диаграммой называют совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени одной и той же частоты и построенные с соблюдением правильной ориентации их относительно друг друга по фазе.

Задачи для самостоятельного решения (к главе 4)

1. Записать в полярной и алгебраической формах комплексные амплитуды напряжений и токов, мгновенные значения которых:

1)

2)

3)

4)

Ответ: 1)

2)

3)

4)

2. Разложить на действительную и мнимую составляющие следующие комплексные числа:

1) 2)3)4)5)6)

7) 8)9)10)11)

Ответ: 1) 4,33 + j2,5; 2) 3,42 + j9,4; 3) – 0,0347 + j0,197; 4) – 0,0345 + j0,00607;

5) – 2,41 – j64,7; 6) – 11,2 – j27,8; 7) 0,174 – j1,99; 8) – j190 + 329,

9) 0,29710^-3 – j0,017; 10) – 1000 – j34,9; 11) 15 + j0,175.

3. Вычислить комплекс: подставить его в полярной и алгебраической формах

О т в е т:

4. Вычислить комплекс представить его в полярной и алгебраической формах.

О т в е т:

30