
- •5. Расчет простейших цепей при синусоидальных токах и напряжениях
- •5.1. Общие и методические замечания
- •5.2. Электрическая цепь синусоидального тока и ее схема
- •5.3. Ток и напряжение при последовательном соединении r, l, с
- •5.4. Комплексное сопротивление
- •5.5. Ток и напряжения при параллельном соединении r, l, с
- •5.6. Комплексная проводимость
- •5.7. Смешанное соединение приемников
- •5.8. Пассивный двухполюсник
- •Р е ш е н и е
- •Р е ш е н и е
- •5.9. Мощность в цепи синусоидального тока
- •5.10. Расчет мощности в цепи переменного тока. Баланс мощности
- •5.11. Измерение активной мощности ваттметром
- •Задачи для самостоятельного решения (к главе 5)
5.8. Пассивный двухполюсник
Пассивный двухполюсник (см. рис. 5.11) может быть представлен двумя эквивалентными схемами.
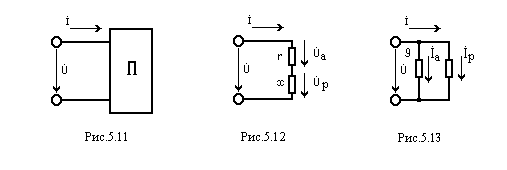
Первая схема представляет собой последовательное соединение активного и индуктивного элементов (рис. 5.12); вторая – параллельное соединение элементов только с активной и реактивной проводимостями (рис. 5.13).
Если известны параметры первой схемы, то по ним можно определить параметры второй и наоборот.
Пусть
известно
![]()
Тогда
![]()
итак
![]()
Пусть
известна
![]()
Тогда
![]()
Откуда
![]()
Следует обратить внимание на то, что мнимая часть комплексной проводимости, имеющая индуктивный характер всегда отрицательна, а емкостная – положительна. И еще одно существенное замечание.
При переходе от последовательной схемы замещения к параллельной оказывается, что активная проводимость g зависит не только от активного сопротивления r, но и от реактивной составляющей полного сопротивления x = L, т. е. зависят от частоты; реактивная проводимость b зависит и от величины r. То же самое можно сказать и о переходе от параллельной схемы замещения к последовательной.
Переход от одной схемы замещения к другой не изменяет величину напряжения и тока на входе пассивного двухполюсника. Реактивное сопротивление пассивного двухполюсника
(рис. 5.11) может быть или индуктивное, или емкостное. Поэтому на эквивалентной схеме
(рис. 5.12) сопротивление х показано условно прямоугольником.
Напряжение
![]() можно разложить на составляющие
можно разложить на составляющие
![]()
где
![]() – составляющая, совпадающая по фазе с
током, называется активной составляющей
напряжения;
– составляющая, совпадающая по фазе с
током, называется активной составляющей
напряжения;
![]() –составляющая,
сдвинутая по фазе относительно тока на
угол /2,
называется реактивной составляющей
напряжения.
–составляющая,
сдвинутая по фазе относительно тока на
угол /2,
называется реактивной составляющей
напряжения.
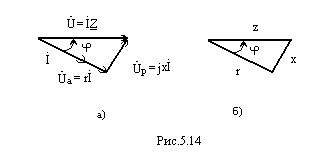
Составляющие
![]() и
и![]() можно рассматривать как напряжения на
элементахr
и
х
эквивалентной схемы. На рис. 5.14 а
представлена векторная диаграмма
двухполюсника (pиc.
5.11) для случая, когда
> 0, т. е. х
– индуктивное
сопротивление.
можно рассматривать как напряжения на
элементахr
и
х
эквивалентной схемы. На рис. 5.14 а
представлена векторная диаграмма
двухполюсника (pиc.
5.11) для случая, когда
> 0, т. е. х
– индуктивное
сопротивление.
Треугольник,
образованный векторами
![]() ,
,
![]() ,
,
![]() ,
со сторонами, пропорциональнымиz,
r
и |x|,
называется треугольником напряжений.
Подобный ему треугольник, стороны
которого в произвольно выбранном
масштабе равны сопротивлениям z,
r
и |x|
(рис. 5.14б),
называется треугольником сопротивлений.
,
со сторонами, пропорциональнымиz,
r
и |x|,
называется треугольником напряжений.
Подобный ему треугольник, стороны
которого в произвольно выбранном
масштабе равны сопротивлениям z,
r
и |x|
(рис. 5.14б),
называется треугольником сопротивлений.
Из треугольника напряжений следует, что
![]()
Другая эквивалентная схема того же двухполюсника, состоящая из параллельного соединения проводимостей g и b, показана на рис. 5.13. Поскольку в общем проводимость b .может быть или индуктивной, или емкостной, на эквивалентной схеме она изображается условно прямоугольником (рис. 5.13). Ток на входе двухполюсника (рис. 5.13) можно разложить на составляющие
![]()
где
![]() – составляющая, совпадающая то фазе с
напряжением, называется активной
составляющей тока;
– составляющая, совпадающая то фазе с
напряжением, называется активной
составляющей тока;
![]() –составляющая,
сдвинутая по фазе относительно напряжения
на угол /2,
называется реактивной составляющей
тока; напомним: в нашем случае для
пассивного двухполюсника (рис. 5.11)
принято, что х
– индуктивное
сопротивление. Составляющие
–составляющая,
сдвинутая по фазе относительно напряжения
на угол /2,
называется реактивной составляющей
тока; напомним: в нашем случае для
пассивного двухполюсника (рис. 5.11)
принято, что х
– индуктивное
сопротивление. Составляющие
![]() и
и![]() можно рассматривать как токи в элементахg
и b
эквивалентной схемы.
можно рассматривать как токи в элементахg
и b
эквивалентной схемы.
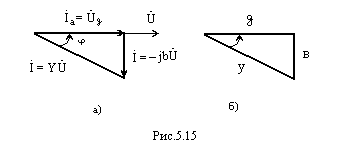
Треугольник,
образованный векторами
![]() ,
,![]() и
и![]() (рис. 5.15а)
со сторонами, пропорциональными у,
g, |b|,
называется треугольником токов. Подобный
ему треугольник, стороны
которого
в произвольно выбранном масштабе равны
проводимостям у,
g b,
называется треугольником проводимостей
(рис. 5.15 б).
(рис. 5.15а)
со сторонами, пропорциональными у,
g, |b|,
называется треугольником токов. Подобный
ему треугольник, стороны
которого
в произвольно выбранном масштабе равны
проводимостям у,
g b,
называется треугольником проводимостей
(рис. 5.15 б).
Из
треугольника токов имеем
![]()
Рассмотрим несколько примеров
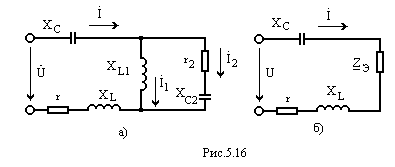
Пример 5.2. Для схемы рис.5.16 а известно:
![]()
Определить
токи
![]() ,
,![]() и
и![]() .
.
