5.5. Ток и напряжения при параллельном соединении r, l, с

Рассмотрим схему, к которой приложено напряжение

Схема состоит из (параллельного соединения элементов r, L и С (рис. 5.7).

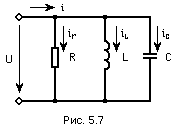
При параллельном соединении элементов напряжение, приложенное к каждому элементу, имеет одно и то же значение. Определим токи во всех ветвях.

По первому закону Кирхгофа

Или

Вводя для заданного синусоидального напряжения изображающее его комплексное напряжение , применим для каждой ветви закон Ома в комплексной форме. Тогда получим

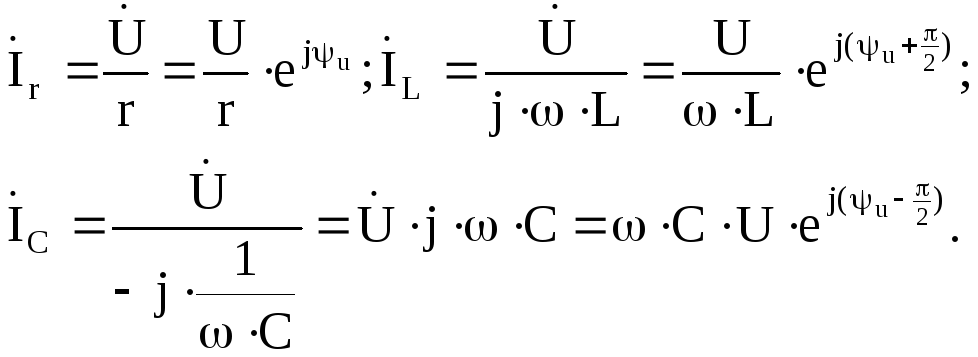
Из полученных выражений видно, что ток в сопротивлении совпадает по фазе с напряжением, ток в катушке индуктивности отстает по фазе от напряжения на угол /2, а ток в емкости опережает напряжение по фазе на /2.

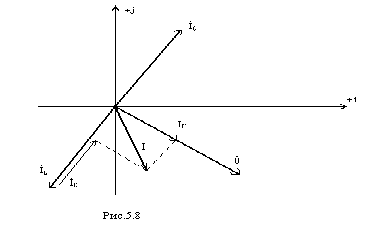
Векторная диаграмма напряжения и токов показана на рис. 5.8, где принято, что Подставив выражения комплексных токов в уравнение первого закона Кирхгофа, найдем, что

или

3десь – комплексная проводимость.

Под разностью фаз напряжения и тока понимается (по определению) величина  = _u - _i и, следовательно, _i = _u - . Поэтому аргумент комплексной величины в квадратных скобках следует обозначать – :

где

или

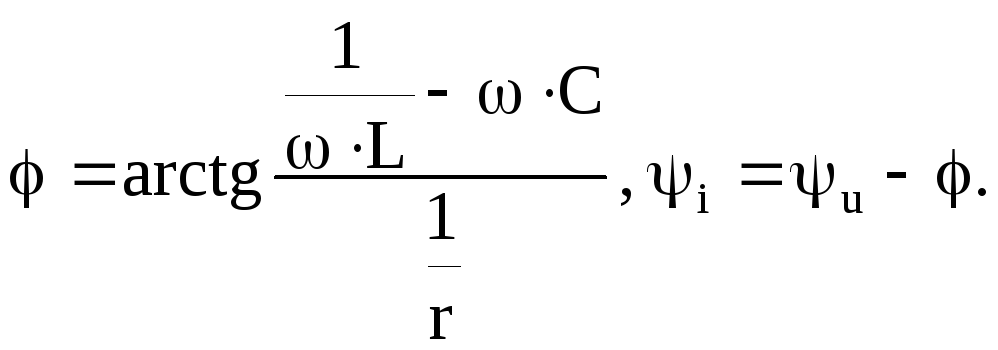
Таким образом, определены амплитуда и начальная фаза_i, тока на входе

схемы

5.6. Комплексная проводимость

Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению

где – величина, обратная полному сопротивлению и называемая полной проводимостью.

Комплексная проводимость и комплексное сопротивление взаимно обратны. Комплексную проводимость можно представить в виде где – вещественная часть комплексной проводимости, называется активной проводимостью. – значение мнимой части комплексной проводимости, называется реактивной проводимостью. При этом

Для схемы, представленной на рис. 5.7, комплексная проводимость

Где и называются соответственно активной, индуктивной и емкостной проводимостями.

Реактивная проводимость b = b_L – b_C.

Индуктивная (b_L) и емкостная (b_C) проводимости – арифметические величины, а реактивная проводимость (b) - алгебраическая величина и может быть как больше, так и меньше нуля, или равна нулю. Реактивная проводимость в ветви, содержащей только индуктивность, равна индуктивной проводимости b_L, а реактивная проводимость в ветви, содержащей только емкость, равна емкостной проводимости с обратным знаком, т. е. – b_C. Единица проводимости – Сименс (См).

5.7. Смешанное соединение приемников

Токи в цепях со смешанным соединением приемников обычно рассчитываются путем преобразования схем.

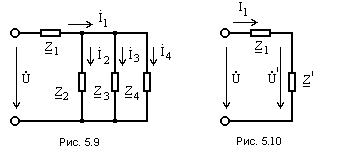
Пусть заданы все элементы схемы (рис. 5.9) и напряжение на ее входе; требуется определить токи во всех ветвях. Заменим параллельно соединенные приемники энергии одним эквивалентным с проводимостьюгдеили сопротивлением . После этого преобразования схема будет состоять из двух последовательно соединенных сопротивлений и (рис. 5.10). Ее эквивалентное сопротивление .

Ток в неразветвленной части цепи

Напряжение на разветвлении

Токи в параллельно соединенных приемниках: