
- •5. Расчет простейших цепей при синусоидальных токах и напряжениях
- •5.1. Общие и методические замечания
- •5.2. Электрическая цепь синусоидального тока и ее схема
- •5.3. Ток и напряжение при последовательном соединении r, l, с
- •5.4. Комплексное сопротивление
- •5.5. Ток и напряжения при параллельном соединении r, l, с
- •5.6. Комплексная проводимость
- •5.7. Смешанное соединение приемников
- •5.8. Пассивный двухполюсник
- •Р е ш е н и е
- •Р е ш е н и е
- •5.9. Мощность в цепи синусоидального тока
- •5.10. Расчет мощности в цепи переменного тока. Баланс мощности
- •5.11. Измерение активной мощности ваттметром
- •Задачи для самостоятельного решения (к главе 5)
5.4. Комплексное сопротивление
Отношение комплексного напряжения к комплексному току называется комплексным сопротивлением
![]()
где
![]() – отношение
действующего или амплитудного напряжения
соответственно к действующему или
амплитудному току называется полным
сопротивлением. Полное сопротивление
равно модулю комплексного сопротивления.
Аргумент комплексного сопротивления
равен разности фаз напряжения и тока,
т. е.
– отношение
действующего или амплитудного напряжения
соответственно к действующему или
амплитудному току называется полным
сопротивлением. Полное сопротивление
равно модулю комплексного сопротивления.
Аргумент комплексного сопротивления
равен разности фаз напряжения и тока,
т. е.
![]() .
.
Комплексное сопротивление можно представить в виде
![]()
где r = zcos – вещественная часть комплексного сопротивления, называется активным сопротивлением; x = zsin – значение мнимой части комплексного сопротивления, называется реактивным сопротивлением. Очевидно, что
![]()
Для схемы, представленной на рис. 5.3, комплексное сопротивление
![]()
причем
реактивное сопротивление
![]() где
где![]() называют соответственно индуктивным
и емкостным сопротивлениями. Индуктивное
сопротивление связывает между собой
амплитуды напряжения на индуктивности
и тока
называют соответственно индуктивным
и емкостным сопротивлениями. Индуктивное
сопротивление связывает между собой
амплитуды напряжения на индуктивности
и тока![]()
Индуктивное
сопротивление прямо пропорционально
частоте тока. Это объясняется тем, что
напряжение на индуктивности пропорционально
скорости изменения тока
![]()
Емкостное сопротивление связывает между собой амплитуды напряжения на емкости и тока
![]()
Емкостное
сопротивление обратно пропорционально
частоте тока. Эту зависимость от частоты
легко пояснить, если считать заданным
напряжение на зажимах емкости, а искомой
величиной ток
![]() .
Ток прямо пропорционален скорости
изменения напряжения на зажимах емкости
uc,
следовательно, емкостное сопротивление
обратно пропорционально частоте
напряжения.
.
Ток прямо пропорционален скорости
изменения напряжения на зажимах емкости
uc,
следовательно, емкостное сопротивление
обратно пропорционально частоте
напряжения.
Следует обратить внимание на то, что индуктивное и емкостное сопротивления являются величинами арифметическими – положительными, а реактивное сопротивление x = xL – xC – величина алгебраическая и может быть больше, меньше нуля и равная нулю.
Для ветви, содержащей только индуктивность, реактивное сопротивление х равно индуктивному сопротивлению xl, а реактивное сопротивление х ветви, содержащей только емкость, равно емкостному сопротивлению, взятому со знаком минус, т. е. – xс.
Для ветвей, каждая из которых содержит только сопротивление r, только индуктивность L или только емкость С, комплексные сопротивления соответственно равны
![]()
Сопротивления
![]() – измеряются в омах.
– измеряются в омах.
Размерность
![]()
При
вычислении индуктивного сопротивления
подставляют в
![]() величинуС
в [Гн
и тогда xL
- .получают в омах.
величинуС
в [Гн
и тогда xL
- .получают в омах.
Размерность
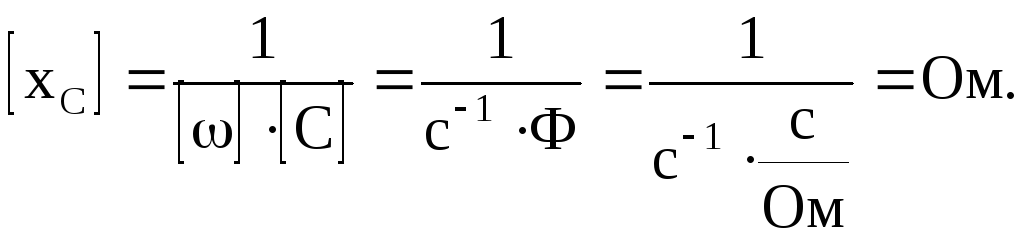
При
вычислении емкостного сопротивления
подставляют в
![]() величинуС
в
[Ф]
и тогда xс
получают в омах.
величинуС
в
[Ф]
и тогда xс
получают в омах.
Пример
5.1.
Дано: цепь рис. 5.3;
![]() В;
С
= 5 мкФ,
r
= 15 Ом,
L
= 12 мГн.
В;
С
= 5 мкФ,
r
= 15 Ом,
L
= 12 мГн.
Определить мгновенный ток i, мгновенное напряжение на конденсаторе и на катушке индуктивности, построить векторную диаграмму.
Решение
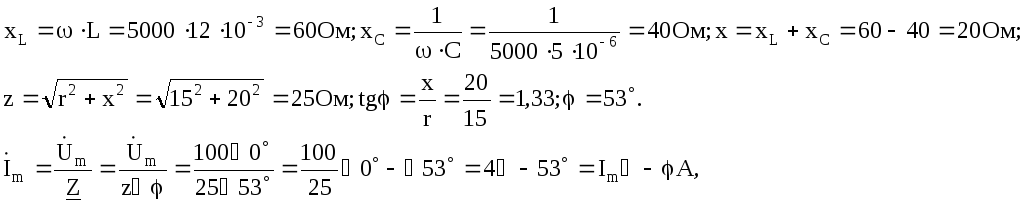
где
![]()
Мгновенное
значение тока
![]()
Напряжение
на емкости
![]()
где
![]()
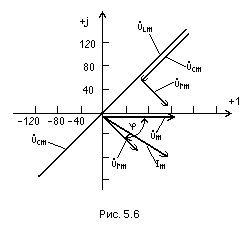
Напряжение на емкости отстает от тока по фазе на 90°. Мгновенное значение
![]() напряжение
на катушке индуктивности
напряжение
на катушке индуктивности
![]()
где
![]()
Напряжение на катушке индуктивности опережает ток по фазе на 90°.
Мгновенное
значение
![]()
Напряжение
на сопротивлении
![]() .
.
Построим векторную диаграмму токов и напряжений для максимальных значений (рис. 5.6)
![]()
