3.4. Матричная форма записи законов Ома и Кирхгофа
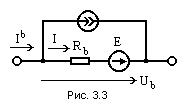
Сначала введем понятие обобщенной ветви (рис. 3.3).Для нее можно записать по первому закону Кирхгофа
(3.6)
И по обобщенному закону Ома
(3.7)
Напряжение на .резисторе ветви R в по закону Ома
(3.8)
Или
для тока через проводимость ветви
(3.9)
Закон Ома в матричной форме
(3.10)
или
(3.11)
где U и I – столбцовые матрицы, число строк которых совпадает с числом ветвей схемы, а
и
причемk
равно числу ветвей схемы.
Например, для схемы рис. 3.1
а
Обобщенный закон Ома в матричной форме, исходя из (3.7), получим в виде
где U в и I в – столбцовые матрицы, число строк которых совпадает с числом ветвей схемы.
Для схемы рис. 3.1
Вводится понятие узловой матрицы [А].
Узловая матрица – это прямоугольная матрица, строки которой соответствуют узлам, а столбцы – ветвям направленного графа схемы.
Число строк матрицы равно числу независимых узлов. Элементы матрицы а ij, где (i – номер строки, j – номер столбца, принимают значения 1, – 1 или 0.
Элементы а ij = 1, если ветвь j соединена с узлом i и направлена от него.
Элементы а ij = - 1, если ветвь j соединена с узлом i и направлена k этому узлу. Элементы а ij = 0, если ветвь j не соединена с узлом i.
Например, в схеме рис. 3.1 и 3.2
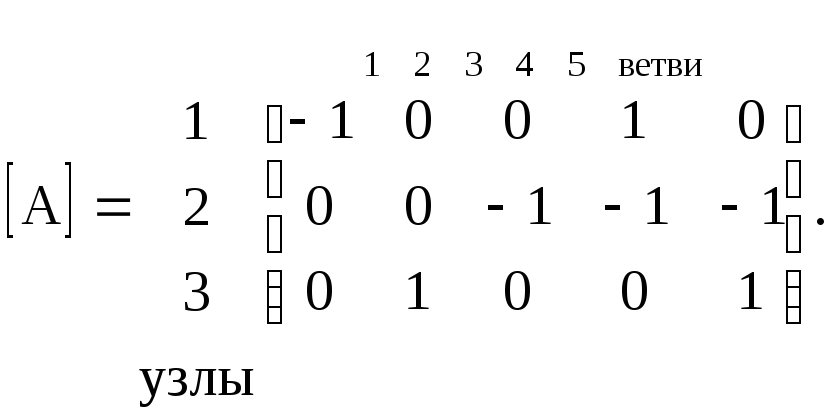(3.13)
С помощью матрицы [А] запишем первый закон Кирхгофа с учетом (3.6)
(3.14)
или
(3.15)
где [J] – столбцовая матрица источников тока, число строк которой совпадает с числом ветвей схемы.
Для схемы рис. 3.1 [J] = [0 0 0 – J J] T , т. е. ток источника тока J замыкается по четвертой и пятой ветвям.
Матрица контуров [В] – прямоугольная матрица, строки которой соответствуют контурам, а столбцы – ветвям направленного графа схемы. Число строк равно числу независимых контуров. Элементы матрицы в ij, где i – номер строки, j – номер столбца, принимают значения 1, –1 или 0. Элементы в ij = 1, если .ветвь j содержится в контуре i и направление ветви совпадает с направлением обхода контура. Элементы в ij = – 1, если ветвь j содержится в контуре i и направление ветви противоположно направлению обхода контура. Элементы в ij = 0, если ветвь j не содержится в контуре i.
Например, в схеме рис. 3.1 и 3.2
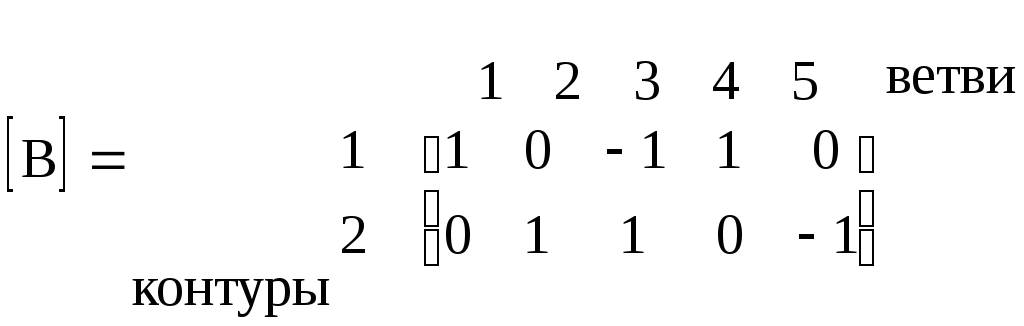(3.16)
С помощью матрицы В запишем второй закон Кирхгофа с учетом (3.12)
(3.17)
или
(3.18)
3.5. Матричная форма записи метода контурных токов
Уравнения метода контурных токов выводятся из уравнений, составленных ,по второму закону Кирхгофа. Подставим в матричное уравнение (3.18) уравнение (3.14), соответствующее первому закону Кирхгофа, переписав его предварительно таким образом
(3.19)
(3.20)
или
(3.21)
Можно показать, что с помощью транспонированной контурной матрицы [В]Т токи ветвей схемы [/в] могут быть выражены через матрицу контурных токов [/к]
(3.22)
где [/к]–столбцовая матрица контурных токов. Тогда выражение (3.21) примет вид
(3.23)
или в более компактной форме
(3.24)
.где
–матрица
контурных сопротивлений;
– матрица контурных ЭДС.
Матрицы уравнения (3.23) более просты для составления, поэтому уравнением (3.23) пользуются при решении на ЭВМ.
После решения уравнения (3.23) относительно контурных токов схемы решают последовательно уравнение (3.22) относительно токов ветвей и (3.19) относительно токов в резисторах.
Пример 3.1. В схеме рис. 3.1 определить токи в резисторах методом контурных токов, если
E1 = 48 В; R1 = 4 Ом;
E2 = 10 В; R2 = R5 = 6 Ом;
E3 = 40 В; R3 = 1 Ом;
J = 2 А; R4 =2 Ом.
Р е ш е н и е
1. Запишем матрицы для решения уравнения (3.23), исходя из графа схемы (рис. 3.2). Римскими цифрами I и II обозначены контуры. Указаны направления обхода контуров.
Контурная
матрица
Диагональная
матрица сопротивлений ветвей
Транспонированная
контурная матрица
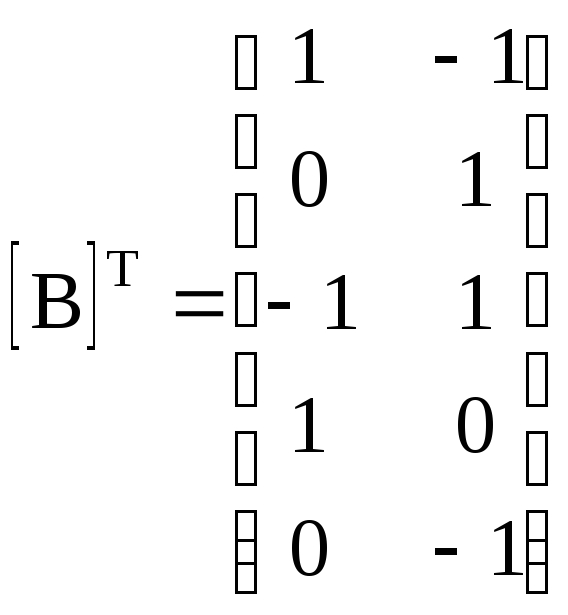
Столбцовые матрицы:
контурных
токов
ЭДС
ветвей
токов
источников токов
2.
Перемножаем матрицы [В]
и [Rв]
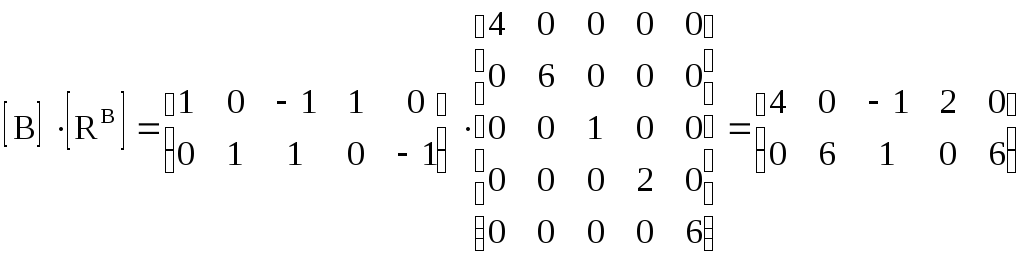
3. Получаем матрицу контурных сопротивлений
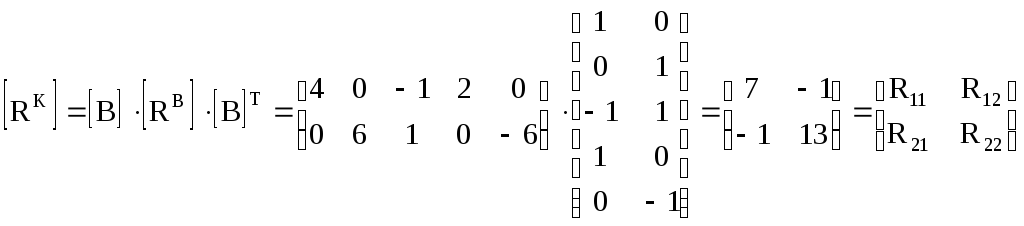
где
R ik – собственные и взаимные сопротивления контуров.
4. Запишем матрицу контурных ЭДС, воспользовавшись ранее найденным произведением матриц [В] на [RB]
5. Далее рассмотрим матричное решение уравнения (3.24) с помощью обратной матрицы [RK]-1.
Для этого умножим слева на матрицу [RK]-1 все слагаемые уравнения (3.24)
Обратная
матрица
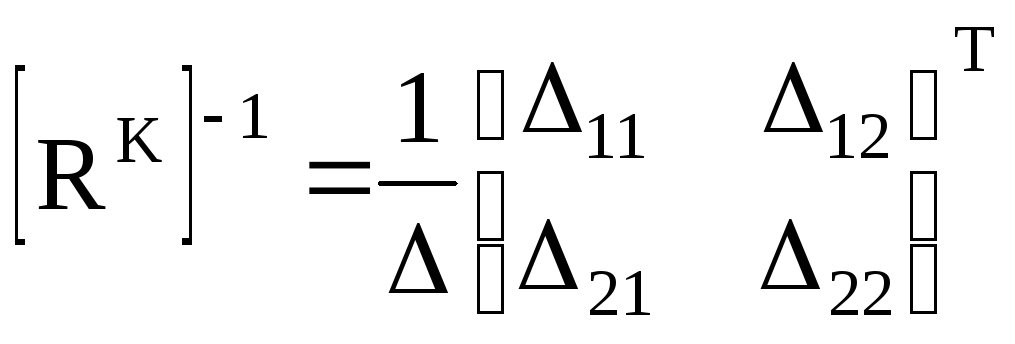
где
- определитель матрицы [RK];
mn
– алгебраические дополнения;
Отсюда
6.
Определим контурные токи
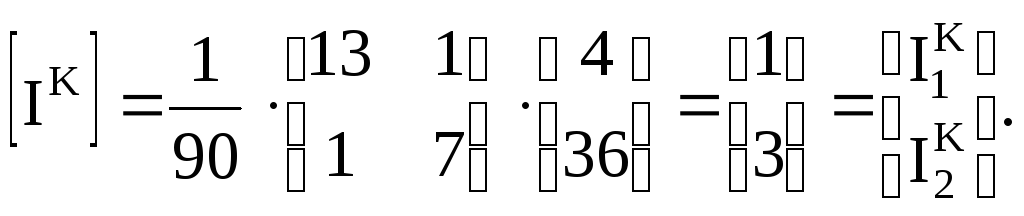Следовательно
I1K = 1 А; I2K = 3 А.
7. Определим токи в ветвях схемы. Решаем уравнение (3.22)
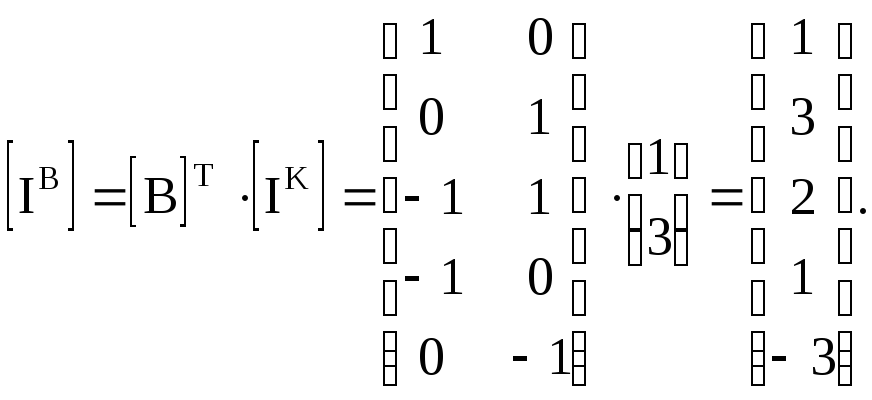
8.
Определим токи в резисторах (3.19)
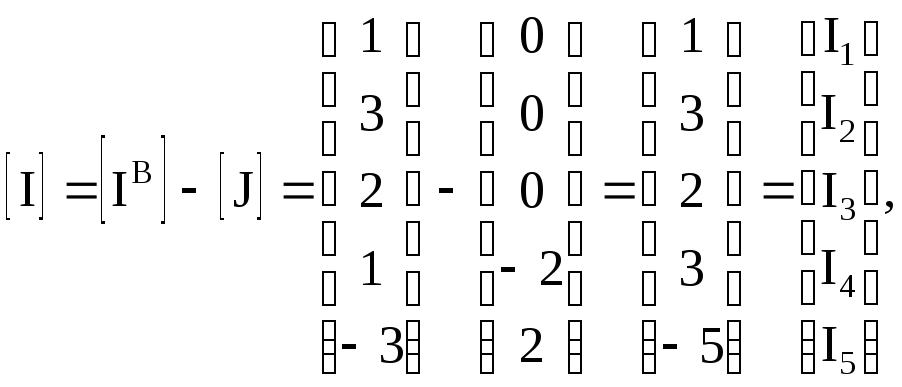
т. е. I1 = 1 A, I2 = 3 A, I3 = 2 A, I4 = 3 A, I5 = - 5 A,