Р а б о т а № 3 Определение коэффициента внутреннего трения воздуха и его зависимости от температуры

Цель работы: экспериментальное определение коэффициента внутреннего трения воздуха.

Принадлежности: манометр с капилляром, сосуд с краном, мерный стакан, секундомер.

Теория

Хаотичность теплового движения молекул газа и непрерывные соударения приводят к постоянному перемещению частиц, изменению их скорости и энергии.

Если в газе существует пространственная неоднородность плотности, температуры или скорости упорядоченного движения, то движение молекул выравнивает эти неоднородности. При этом в газе протекают явления переноса. К ним относятся диффузия (направленный перенос массы), теплопроводность (направленный перенос энергии), внутреннее трение или вязкость (направленный перенос количества движения).

Рассмотрим явление внутреннего трения в газах. Если скорость в потоке газа меняется от слоя к слою, то на границе смежных слоев действует сила внутреннего трения, величина которой определяется эмпирической формулой:

, (1)

где – коэффициент внутреннего трения (коэффициент вязкости);

–градиент скорости, характеризующий быстроту изменения скорости от слоя к слою;

S – величина поверхности, на которую действует сила.

Рассмотрим это явление с позиции молекулярно–кинетической теории газов. Выделим два соприкасающихся слоя газа (рис.1).

П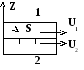усть слои движутся со скоростямиU ₁ и U₂ , U₁ >U₂. Каждая молекула газа участвует в двух движениях: упорядоченном со скоростью U и хаотическом тепловом, средняя скорость которого <v> >> U.

В

Рис.1. Соприкасаю-щиеся слои газа.

следствие хаотического движения происходит непрерывный переход молекул из одного слоя в другой. За времячерез поверхностьS переходит из слоя в слой : из первого во второй и из второго в первый одинаковое число молекул.

, (2)

где n₀ – число молекул в единице объема.

Вследствие неодинаковости скоростей упорядоченного движения U₁ >U₂ молекулы в различных слоях обладают в среднем различным количеством движения. Попав в другой слой, молекула сталкивается с его молекулами. В результате чего она либо отдает избыток своего количества движения (при переходе из слоя 1 в слой 2), либо увеличивает свое количество движения ( при переходе из слоя 2 в слой 1). Из первого слоя за время молекулы унесут во второй слой количество движения:

,

где m – масса молекулы.

За это время из слоя 2 в слой 1 молекулы перенесут количество движения:

.

Изменение количества движения второго слоя будет равно:

. (3)

Согласно основному закону динамики, изменение количества движения равно импульсу действующей силы:

.

Сила F – есть сила внутреннего трения, равная:

. (4)

С учетом выражения (2) выражение (4) приобретает вид:

. (5)

Разность скоростей (U₁ –U₂ ) можно выразить через градиент скорости . Обозначим скорость в месте раздела слоев черезU. Далее учтем, что перенос количества движения осуществляется только теми молекулами, которые находятся от границы раздела слоев на величину средней длины свободного пробега.

Тогда можно записать:

;

.

Откуда разность скоростей равна:

.

С учетом последнего соотношения выражение (5) приобретает вид:

.

Произведение концентрации молекул на массу молекул есть плотность газа:

.

Окончательно получаем:

(6)

Сравнивая полученное выражение с эмпирической зависимостью (1) видим, что молекулярно–кинетическая теория газов позволяет связать величину коэффициента вязкости с параметрами, характеризующими движение молекул:

. (7)

Соотношение (7) позволяет получить по экспериментально определенной величине важную характеристику движения молекул – среднюю длину свободного пробега :

. (8)

Средняя скорость движения молекул зависит от температуры Т и определяется выражением:

, (9)

где R – газовая постоянная,

 – молярный вес.

Плотность газа является функцией давления Р и температуры Т:

. (10)

С учетом соотношений (9) и (10) формула для нахождения средней длины свободного пробега принимает вид:

. (11)

Из формулы (11) видно, что для нахождения средней длины свободного пробега молекул газа необходимо знать величину давления Р и температуры Т. Если известна средняя длина свободного пробега молекул, то можно оценить значение эффективного диаметра молекул .

Как следует из молекулярно–кинетической теории газов, величина  связана с эффективным диаметром следующим соотношением:

, (12)

где k– постоянная Больцмана; откуда:

. (13)

Значение эффективного диаметра молекул имеет большое значение при анализе различных физических явлений, таких как упругое и неупругое рассеяние частиц (фотонов, нейтронов и др.)

Существуют различные способы определения коэффициента вязкости газов. В настоящей работе применяется метод капилляра.

Рассмотрим движение воздуха в трубке круглого сечения. При малых скоростях потока движение оказывается ламинарным (слоистым). При увеличении скорости потока движение становится турбулентным и слои перемешиваются. При турбулентном движении скорость в каждой точке быстро меняет величину и направление, сохраняется только средняя величина скорости.

Характер движения газа в трубке определяется безразмерным числом Рейнольдса:

, (14)

где v – скорость потока,

r– радиус трубки,

- плотность движущейся среды,

 – ее коэффициент вязкости.

В гладких трубках круглого сечения переход от ламинарного движения к турбулентному происходит при R =1000.

При ламинарном течении объем V газа, протекающий за время t по трубе длины l, определяется формулой Пуазейля:

. (15)

В этой формуле( Р₁ – P₂) - разность давлений в двух выбранных сечениях 1 и 2, расстояние между которыми равно. ВеличинуQ обычно называют расходом. Формула (15) позволяет определить вязкость газа по его расходу, т.е. :

. (16)

Выясним условия, при которых справедлива формула (15). Как уже было сказано выше, для этого прежде всего необходимо, чтобы с достаточным запасом выполнялось неравенство R<1000. Необходимо также, чтобы при течении сквозь трубку не происходило существенного изменения удельного объема воздуха (при выводе формулы удельный объем жидкости считается постоянным). Для газа это предположение не выполняется лишь в тех случаях, когда перепад давления вдоль трубки мал по сравнению с самим давлением.

В нашем случае давление газа равно атмосферному (10 см водяного столба), а перепад давлений составляет не более 5 см водяного столба, т. е. 0,5 от атмосферного.