252067, Киев, бульвар и.Лепсе, 4.

Арендное предприятие « РОСТОК »

Главному конструктору

Лабораторная работа № 8,9

Теоретические основы электротехники

Лабораторная работа № 8. Несимметричный пассивный четырехполюсник.

Лабораторная работа № 9. Симметричный пассивный четырехполюсник.

Теоретическая часть.

Несимметричный пассивный четырехполюсник.

Симметричный пассивный четырехполюсник.

Четырехполюсником называется часть электрической цепи, имеющая две пары зажимов, причем к одной паре зажимов (входной) присоединяется источник энергии, а к другой паре (выходной)- приемник энергии. Основной смысл теории четырехполюсников заключается в том, что, пользуясь некоторыми обобщенными параметрами электрической цепи, можно аналитически связать и исследовать напряжения и токи на входе и выходе схемы, не производя расчетов токов и напряжений внутри самой схемы.Так, в качестве четырехполюсника может быть представлена линия электропередачи, электрические фильтры, трансформатор, усилитель, линия связи и любое другое устройство, включенное между источником и приемником электрической энергии.

Четырехполюсники могут быть классифицированы следующим образом:

1.Линейные - все элементы четырехполюсника линейные.

2.Нелинейные - хотя бы один элемент нелинейный.

3.Активные - внутри четырехполюсника содержатся нескомпенсированные источники энергии.

4.Пассивные - внутри четырехполюсника не содержатся источники энергии, либо источники взаимокомпенсированы, т.е. при отключении четырехполюсника напряжения на входных и выходных зажимах отсутствуют.

5.Симметричные - токи и напряжения в цепи не изменяются при перемене местами входных и выходных зажимов четырехполюсника.В противном случае четырехполюсник не симметричный.

При рассмотрении четырехполюсников необходимо обратить внимание на опре – деление четырех обобщенных (первичных) параметров, три из которых незави – симы. Определение параметров проводится расчетным путем, если известна схе – ма четырехполюсника, либо экспериментальным способом по двум режимам, например, режимам короткого замыкания (КЗ) и холостого хода (ХХ). Характеристическое сопротивление и постоянная передачи являются вторичнымипараметрами четырехполюсника, значения которых позволяет судить о прохож– дении сигнала от источника к нагрузке.

Основные уравнения четырехполюсника.

Четырехполюсник принято изображать как показано на рис.1, где входные,

а – выходные зажимы. Положительные направления токов,и

напряжений ,показаны на рис.1, при этом положительное направление

потока энергии на зажимак четырехполюснику, на зажимах– от него

к нагрузке .Источник энергии подключен к входным зажимам.

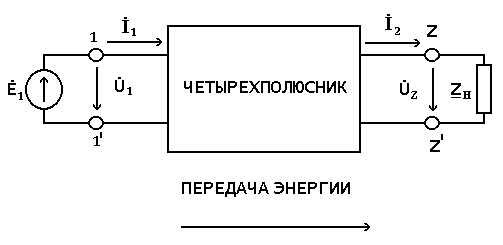Рис.1.

Уравнения связи ,,,в четырехполюснике.

Для понимания математического отображения процессов происходящих в

четырехполюснике найдем уравнения, связывающие между собой токи и

напряжения,,,.

Заменим нагрузкуисточником ЭДС=, направленным встречно току

/по теореме компенсации /.

Используем метод контурных токов, при этом выбираем входной и выходной

контуры с контурными токами,и контурными ЭДС,.

В результате имеем следующие уравнения:

+++ ........+=

+++........+= –

+++........+= 0

............................................................................

где – собственные ( приi = j ) и общие ( при ij ) сопротивления внутри

четырехполюсника.

Решая полученную систему уравнений ( относительно ,) получим

=–

=– ,

где =,=

–определитель системы, порядок определителя равен числу независимых контуров «n»,

–алгебраические дополнения, получающиеся из определителя , путем вычеркивания в немi–строки и j–го столбца и умножения вновь полученного определителя на (-1).

Отношениеназывается проводимостью и обозначается отсюда

=; –=;

=; –=;

где – собственные ( приi = j ) и взаимные ( при ij ) проводимости четырехполюсника.

Отсюда уравнения принимают вид

= +

= +(1)

Для линейного пассивного четырехполюсника выполняется условие

=, поэтому = –.

Решим систему уравнений (1) относительнои

Получим

= +

= +(2)

где =;=;=;=;

= = –

при этом = –

Решим систему уравнений (1) или (2) относительноиполучим систему уравнений типа «А »

= А+ В

= С+D(3)

где

А = =,

В = = –

С = – =

D = = –

Коэффициент В – имеет размерность сопротивления

С – проводимость

А и В – безразмерные

Учитывая взаимные свойства четырехполюсника, т.е.

= – или= –получаем

AD – BC = – + =1 (4)

Отсюда, в каждой системе уравнений (1), (2), (3), три коэффициента являются независимыми, четвертый определяется согласно (4), следовательно четырехполюсник можно характеризовать тремя независимыми параметрами.

Уравнение четырехполюсника при питании со стороны выходных зажимов.

Вслучае перемены передачи электрической энергии, а именно при передаче энергии справа налево, положительные направления токов и напряжений принимаются согласно рис.2.

Рис.2.

Уравнения четырехполюсника по рис.2 имеют вид :

= А– В

–= С–D

Решая систему уравнений относительно,, получим

= D+ В

= С+A(5)

Сопоставим (5) и (3) заключаем , что А и D меняются местами.

Симметричный четырехполюсник.

Для симметричного четырехполюсника

= ,=,

а следовательно

А=D и А² – ВС =1

Следовательно, симметричный четырехполюсник характеризуется двумя независимыми параметрами.

Экспериментальное определение коэффициентов четырехполюсника А,В,С,D.

Определение происходит путем режимов ХХ и КЗ при наличии питании со стороны первичных и вторичных зажимов.

1.Питание со стороны входных зажимов в режиме ХХ при этом

= ∞, = 0, = , = ,

Из уравнений (3) имеем

А = , С =

Входное сопротивление относительно зажимов 1- 1^/ ( рис.1).

= =

2.Питание со стороны входных режимов в режиме КЗ вторичных зажимов, при этом

= 0, = , =0, = ,

^{В = ,D =}

^{Входное сопротивление}

⁼⁼

3.Питание со стороны выходных зажимов в режиме КЗ входных зажимов

( рис.2),при этом

= 0, =, =0, = ,

Входное сопротивление относительно зажимов 2-2^/

==

^{4.Питание со стороны выходных зажимов в режиме ХХ входных зажимов}

^{при этом}

= ∞, =,=0,=

= =

Таким образом ,

==АD – BC =1

⁼⁼