
Сопромат 23614
.pdf
Задача № 1.
Для заданной схемы поперечного сечения стержня (балки), состоящей из стандартных прокатных профилей требуется:
1.Определить положение центра тяжести;
2.Найти величины осевых и центробежного моментов инерции относительно случайных осей, проходящих через центр тяжести (Xc;Yc);
3.Определить направление главных центральных осей;
4.Найти величины моментов инерции относительно главных центральных осей;
5.Определить моменты сопротивления и радиусы инерции;
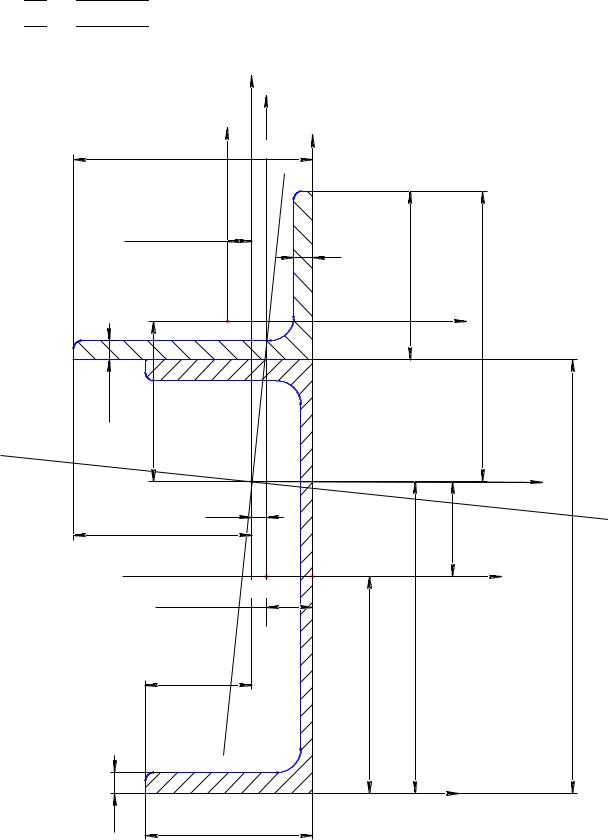
6.Вычертить сечение в масштабе 1:2 и указать на нем все размеры в числах и все оси.
Исходные данные. Швеллер № 18, уголок неравнополочный 110×70×8.
Решение.
Выписка из таблиц сортамента:
1)Швеллер № 18: А=20,7 см2; Ix=1090 см4; Iy=86 см4; z0=1.94 см.
2)Уголок 110×70×8: А=12,3 см2; Iy=152 см4; Ix=48.7 см4; Iu min=28.8 см4; y0=1.6 см; x0=3,57 см (выбраны с учетом расположения уголка).
Вкачестве вспомогательных примем оси, проходящие по внешним
сторонам швеллера (оси xB, yB).Координаты центра тяжести сечения:
∑ |
( |
) |
( |
) |
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
∑
∑
Осевые моменты инерции:
Центробежные моменты инерции:
– для швеллера Ix1y1=0 (есть оси симметрии);
|
|
|
|
|
|
– для уголка |
√( |
) ( |
) |
, |
|
знак минус – в связи с положением уголка в сечении; |
|
|
|||

– для всего сечения:
( |
) |
( |
) |
Главные моменты инерции сечения:
|
|
|
|
) √( |
|
|
|
|
|
|
|
|
|
|
|
|
[( |
|
) |
] |
|
[( |
) √( |
) |
( |
) ] |
|||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Положение главных центральных осей сечения:
( )
( )
Угол α отсчитывается от оси x, так как Ix > Iy.
Т. к сечение не симметричное, то моменты сопротивления будут:
Радиус инерции сечения относительно осей:
√∑ √
√∑ |
√ |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
y1 |
|
|
|
|
y2 |
|
|
|
|
|
100 |
YB |
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
n2 =10,3 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
70 |
120,5 |
|
|
|
C2 |
|
|
|
|
|
|
|
x2 |
|
8 |
|
|
|
|
|
=66,5 |
|
|
|
|
|
2 |
|
C |
|
x |
|
m |
|
|
||
|
|
|
n1 =6 |
=39,5 |
180 |
|
|
|
|
|
|
|
74,6 |
|
|
|
u |
|
|
|
|
1 |
|
|
|
|
|
m |
|
|
|
19,4 |
C1 |
|
x1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
90 |
|
|
|
44,6 |
|
|
|
|
|
|
|
129,5 |
|
|
8,7 |
|
70 |
|
XB |
|
|
|
|
||
|
|
|
|
|
|
|
|
Размеры указаны в милиметрах. |
|
||
Задача № 2.
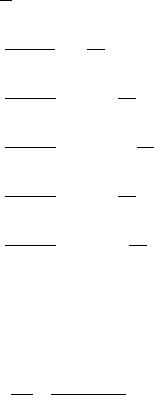
Стальной стержень находится под действием силы F и собственного веса. Необходимо построить эпюры нормальных сил, нормальных напряжений и перемещений поперечных сечений стержня относительно закрепления. Показать в задании определение нормальных сил, напряжений и перемещений в характерных сечениях.
Модуль продольной упругости для стали принять равным Е=2×1011 Па, удельный вес γ=78 кН/м3.
Исходные данные. F=1.1 кН; A=2 см2; a=18 м; b=10 м; c=13м.
Решение.
Разбиваем стержень на участки.
Нормальные силы на границах участков:
По полученным значениям строим эпюру.
Нормальные напряжения на границах участков:
По полученным значениям строим эпюру.
Изменение длины участков стержня:
Абсолютное изменение длины стержня:
Перемещения в сечениях:
|
|
. |
|
|
|
N, кН |
, МПа |
|
, мм |
|
|
|
0 |
|
|
|
|
|
|
|
1,9 |
9,5 |
|
|
a |
|
|
|
|
|
+ |
|
+ |
|
|
|
|
|
|
|
1,6 |
|
|
0,066 |
|
4 |
|
|
|
|
|
|
|
|
b |
|
|
|
+ |
|
1,3 |
3,25 |
|
0,361 |
|
|
|
|
|
F |
0,2 |
|
1 |
|
c |
|
|
|
|
|
|
0 |
0 |
0,394 |
|
|
|
||
|
|
|
|
|
G |
|
|
|
|
|
Задача № 5. |
|
|
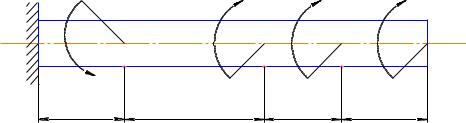
Стальной вал круглого поперечного сечения нагружен внешними моментами в соответствии с |
|||
заданной схемой. Требуется построить эпюру крутящих моментов и из условия прочности |
|||
определить диаметр вала, округлив расчетное значение до ближайшего целого нормированного |
|||
числа. Допускаемое напряжение принять [ ]=80 МПа. |
|
|
|
Для принятого диаметра вала построить эпюру углов закручивания поперечных сечений |
|||
относительно крайнего левого сечения. Определить также наибольший относительный угол |
|||
закручивания (на 1 пог. м). |
|
|
|
Исходные данные. a=1.1 м; b=1.8 м; c=1 м; T1=1.6 кНм; T2=1.5 кНм; T3=2.3 кНм; T4=1.3 кНм. |
|||
Т1 |
Т2 |
Т3 |
Т4 |
1,1 |
1,8 |
1 |
1,1 |
|
Решение. |
|
|
В заделке возникает момент Т0 . |
|
|
|
∑
Для определения крутящих моментов Мк на участках стержня будем рассматривать его левую часть.
По вычисленным значениям Мк строится эпюра.
Преобразуем условия прочности и жесткости к виду, удобному для определения диаметра стержня.
Условие прочности:
|
|
|
|
[ ] |
|
|

√ |
|
√ |
[ ] |
||
Принимаем d=70 мм=0,07 м.
Полярный момент инерции сечения вала.
Определим деформации участков стержня:
Углы поворота характерных сечений (границ участков) равны:
Строим эпюру углов поворота сечений.
Наибольший относительный угол закручивания:
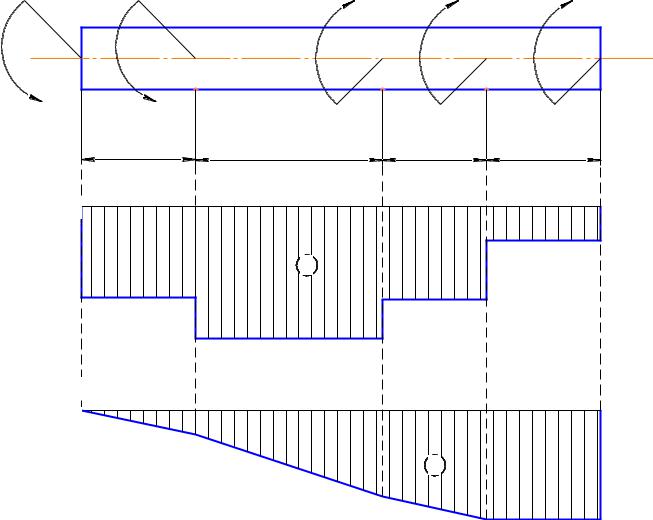
Т0 |
Т1 |
Т2 |
Т3 |
Т4 |
1,1 |
1,8 |
1 |
1,1 |
Мк , кНм |
|
|
|
0 |
|
|
|
|
|
- |
-1,3 |
|
|
|
|
-3,5 |
|
|
-3,6 |
|
|
|
|
|
|
-5,1 |
|
|
|
|
|
0 |
|
|
|
|
-0,9867 |
|
- |
|
|
|
|
|
|
|
-3,339 |
|
|
|
-4,2615 |
Задача № 6.
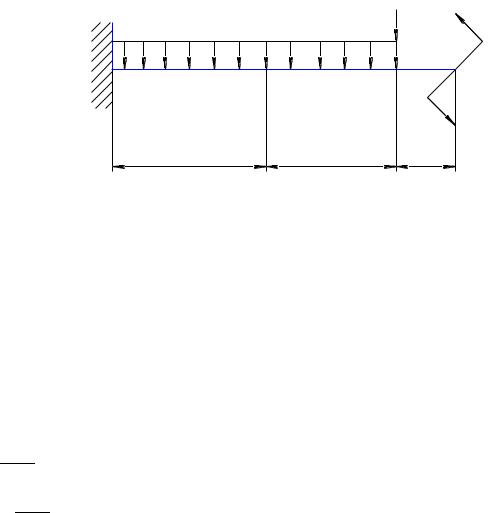
Приведены схемы нагрузки статически определимых балок. Требуется:
1.Определить опорные реакции и построить эпюры поперечных сил и изгибающих моментов. Для каждого участка балки необходимо записать предварительно уравнения определяемых величин для произвольных сечений.
2.В задаче № 6А из условия прочности подобрать номер профиля стальной балки двутаврового сечения. Вычислить для нее максимальные значения нормального и касательного напряжений. Определить прогибы в характерных точках балки (2-3 точки). По найденным значениям построить изогнутую ось балки.
3.В задаче № 6Б из условия прочности подобрать деревянную балку прямоугольного сечения при отношении высоты сечения к ширине 4:1.
Задача № 6А.
Исходные данные. F=12 кН; q=14 кН/м; M=18 кНм; a=2.6 м; b=2.2 м; c=1 м.
q |
|
F |
M |
|
|
||
a |
b |
c |
|
Решение.
Силу, равномерно распределенную вдоль отрезка прямой, заменяем равнодействующей.
( |
) |
( |
) |
Записываем уравнения статики и определяем опорные реакции.
∑
∑
( )
( |
) |
|
( |
) |
|
∑

Проверка.
∑
( |
) |
( |
|
) |
|
|
|
|
|
||||
|
( |
|
) |
( |
|
) |
|
|
|
Эпюра поперечных сил.
Эпюра изгибающих моментов.
|
( |
|
) |
|
|
|
|
|
( |
) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
|
( |
|
) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
( |
) |
|
( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( |
) |
( |
|
|
) |
|
( |
|
|
|
|
|
|
) |
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||
( |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
( |
) |
( |
|
|
|
|
) |
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
Подбор номера двутавра.
| |
[ ]
Выбираем двутавр № 45. Для данного двутавра:
- момент сопротивления сечения Wz=1220 см3; -момент инерции Jz=27450 см4;
-статический момент половины сечения Sz=699 см3; -толщина стенки d=8,6 мм.
Максимальное нормальное напряжение:
