3.2. Интеграл дюамеля [1, 11].

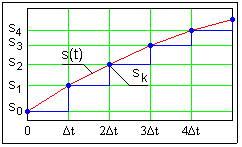
Произвольный аналоговый сигнал s(t) можно представить в дискретной форме с шагом t в виде ступенчатой функций с высотой каждой ступеньки, равной приращению функции s(t) между соседними точками (рис. 3.2.1):

s(t) ≈ s(0)t)+(s₁-s₀)(t-t)+(s₂-s₁)(t-2t)+…= s(0)(t) +(s_k-s_k-1)(t-kt).

Рис. 3.2.1.

где (t) – функция включения. В пределе, для бесконечно малого значения шага дискретизации:

t → , (s_k-s_k-1) → ds = (ds/d)d, kt → ,

получаем формулу динамического представления сигнала посредством функций включения:

s(t)= s(0)(t) +(t-) d

Реакция системы на функцию включения (t) называется её переходной характеристикой и обозначается через g(t). Для линейной системы с переходной характеристикой g(t) входное воздействие (t-) вызывает отклик g(t-), поэтому

s(t)  s(0)(t) + (s_k-s_k-1)g(t-kt).

Переходя к переделу при t → 0, получим выражение, которое называют интегралом Дюамеля:

y(t)= s(0)(t) + s’()g(t-) d (3.2.1)

Тождественная форма:

y(t)= s(0)(t) + s’(t-)g() d (3.2.1’)

Интеграл Дюамеля целесообразно применять, когда известна или легко находится переходная характеристика системы.

Рис. 3.2.1.

Пример расчета выходного сигнала системы на ступенчатый входной сигнал приведен на рис. 3.2.1. Ступенчатая форма сигнала принята для более наглядного представления процесса формирования выходного сигнала. В общем случае, форма входного воздействия может быть произвольной.

3.3. Свертка (конволюция) сигналов [1, 11].

Интеграл свертки. Произвольный сигнал на входе системы с использованием выражений разложения сигнала по единичным импульсам Дирака может быть представлен в виде последовательной линейной комбинации взвешенных единичных импульсов:

y(t) = T[s(t)] = T[s()(t-) d

На основании принципа суперпозиции линейный оператор Т может быть внесен под знак интеграла, т.к. последний представляет собой предельное значение суммы. При этом операция преобразования действует только по переменной t. Отсюда следует:

y(t) = s() Т[(t-)] ds() h(t-) d. (3.3.2)

Этот вариант динамического представления сигнала и является интегралом свертки (конволюции) входного сигнала с импульсной характеристикой системы. Заменой переменных t-= можно убедиться в том, что свертка коммутативна:

s() h(t-) d h() s(t-) d. (3.3.2')

Функция h() называется ядром свертки (kernel) или импульсной характеристикой линейной системы.

Смысл интеграла свертки состоит в том, что входной сигнал представляется сомкнутой последовательностью следующих друг за другом коротких импульсов, площади которых равны значению сигнала в моменты их следования при длительности импульсов, стремящейся к нулевой. Такая последовательность импульсов условно может рассматриваться в виде последовательности дельта-функций с площадями, равными площадям соответствующих импульсов. Реакция системы (3.3.2) находится как сумма реакций на каждый импульс, составляющий входное воздействие.

Аналогично, для дискретных сигналов, где значение t, как правило, принимается равным 1, а индексы k и n выполняют роль номеров отсчетов числовых рядов:

y(k) =h(n) s(k-n). (3.3.2'')

В цифровых методах обработки сигналов функцию h(n) обычно называют оператором свертки, а его размер по числу отсчетов – окном оператора свертки.

Выражения (3.3.2) имеют специальную форму упрощенной математической записи в символическом виде:

y(t) = s(t-) _* h()  s(t) _* h(t).

Сравнением выражений (3.3.2' и 3.3.2'') с выражениями (3.1.3) нетрудно убедиться в их полной идентичности, за исключением нижнего предела интегрирования (суммирования). Это и понятно, так как выражения (3.1.3) были получены при рассмотрении реальной физической системы, работающей в реальном масштабе времени, импульсный отклик которых является односторонним (равен нулю при <0). Для таких систем интегрирование (и суммирование) от - до 0 не имеет смысла. Кроме того, в реальных физических системах импульсный отклик, как правило, отличен от нуля только на определенном интервале, и, соответственно, пределы интегрирования (суммирования) в выражениях (3.3.2' и 3.3.3'') ограничиваются значениями, на которых функции h() и h(n) существует или имеет значимые значения.

Сигналы, обрабатываемые на компьютере, имеют конечную продолжительность. Допустим, сигнал s(k) отличен от нуля только на отрезке от 0 до K включительно ("имеет длину K+1"). Пусть окно оператора свертки h(n) отлично от нуля на отрезке от – N до N (2N+1 отсчет). При подстановке этих сигналов в уравнение свертки, мы получим сигнал y(k), который отличен от нуля на отрезке от − N до K+N включительно. Таким образом, длина выходного сигнала равна 2N+K-1, т.е. сумме длин исходного сигнала и ядра свертки минус один.

Рис. 3.3.1.

Техника выполнения свертки для цифровой системы приведена на рис. 3.3.1. Для вычисления свертки массив одной из функций (s_k - входного или свертываемого сигнала) располагается по ходу возрастания номеров. Массив второй функции (более короткого оператора h_n), строится параллельно первому массиву в обратном порядке (в режиме обратного времени, по ходу уменьшения номеров первого массива). Для вычисления y_k значение h₀ располагается против s_k, все значения s_k-n перемножаются с расположенными против них значениями h_n и суммируются. Результаты суммирования являются выходным значением функции y_k, после чего оператор h_n сдвигается на один номер k вперед (или функция s_k сдвигается ему навстречу) и вычисление повторяется для номера k+1 и т.д.

Рис. 3.3.2.

Для вычисления аналоговой свертки по выражению (3.3.2') функция импульсного отклика реверсируется по своей координате, т.е. строится в режиме обратного времени, и движется относительно функции входного сигнала в сторону возрастания значений t. В каждый текущий момент времени значения обеих функций перемножаются, а произведение интегрируется в пределах окна импульсного отклика. Полученный результат относится к той координатной точке, против которой находится значение импульсного отклика h(0).

На рис. 3.3.2. приведен пример выполнения свертки прямоугольного импульса с импульсным откликом RC-цепи, площадь которого нормирована к 1. Если площадь импульсного отклика h(t) равна 1, то площадь выходного сигнала свертки всегда должна быть равна площади входного сигнала, что можно видеть на верхнем графике рисунка, при этом одномасштабное сравнение входного и выходного сигналов наглядно демонстрирует характер преобразования сигнала в данной системе. На последующих графиках рисунка демонстрируется вычисление результатов свертки в ряде последовательных точек t_i = {3.5, 4, 5, 6, 7} временной оси. В силу отрицательного знака  в аргументах функции s(t-) интегрирование произведения h()s(t-) выполняется назад по времени и может ограничиваться только определенной длиной значимых значений импульсного отклика (которая в данном случае установлена равной r = 4), а результат относится к начальной точке h(0) импульсного отклика. Так как входной сигнал, рассмотренный на рисунке, представляет собой прямоугольный импульс с амплитудой 1, то интеграл свертки в каждой текущей точке расчета равен площади импульсного отклика в пределах границ входного прямоугольного импульса (заполнено точками).

Свойства свертки. Для свертки характерны следующие свойства:

• 1. Дистрибутивность: h(t) _* [a(t)+b(t)] = h(t) _* a(t)+h(t) _* b(t).

• 2. Коммутативность: h(t) _* a(t) _* b(t) = a(t) _* b(t) _* h(t).

• 3. Ассоциативность: [a(t) _* b(t)] _* h(t) = h(t) _* a(t) _* b(t).

Преобразование свертки однозначно определяет выходной сигнал y(t) для установленного значения входного сигнала s(t) при известном значении функции импульсного отклика системы h(t). Обратная задача деконволюции - определение функции s(t) по функциям y(t) и h(t), относится к разряду некорректных, и имеет решение только при вполне определенных условиях. Это объясняется тем, что свертка может существенно изменить частотный спектр сигнала y(t) относительно s(t) и восстановление функции s(t) становится невозможным, если определенные частоты ее спектра в сигнале y(t) полностью утрачены.

Любая практическая система должна быть устойчивой, т.е. для сигналов, конечных по энергии или средней мощности, выходные сигналы также должны быть конечными по этим параметрам. Устойчивость обеспечивается при выполнении условия абсолютной интегрируемости импульсного отклика системы:

|h(t)| dt < .

Для систем с m входами и n выходами аналогично определяются парциальные импульсные отклики h_ij(t), i = {1,2, ... ,n}, j = {1,2, ... ,m}, каждым из которых отображается сигнал на i-м выходе при поступлении сигнала t) на j-й вход. Полная совокупность импульсных откликов образует матрицу:

,

а выражение свертки приобретает вид:

(t) = ()(t-) d

Здесь (и в дальнейшем тексте) жирным шрифтом с "крышкой" выделяются векторные величины.

Системы свертки. Свертка выполняется системой (физическим или программным устройством). Физические системы, работающие в реальном времени, вычисляют текущее значение выходного сигнала по всем прошлым значениям входного сигнала, и не могут иметь в своем распоряжении будущих значений входного сигнала. Операторы таких систем являются односторонними (каузальными). Вышеприведенная, нормированная к 1 по площади, функция RC-цепи h(t) = (1/RC)exp(-t/RC), принятая в качестве системного оператора на рис. 3.3.2, является именно таким односторонним каузальным оператором. При сравнении выходного сигнала такой системы с входным нетрудно заметить, что выходной сигнал сдвигается относительно входного сигнала. Для каузальных систем такой "сдвиг по фазе" существует всегда и не может быть исключен (сигнал на выходе системы не может быть раньше сигнала на ее входе).

Входным сигналом программных систем является сигнал в целом, записанный в память вычислительного устройства. При обработке таких данных в распоряжении системы при вычислении любой текущей точки выходного сигнала имеются как "прошлые" для данной точки, так и "будущие" значения входного сигнала. Это позволяет создавать системы без сдвига фазы выходного сигнала относительно входного. Для создания таких систем без сдвига фазы может использоваться два способа:

Рис. 3.3.3.

1. Первый способ иллюстрирует рис. 3.3.3. Задается система с односторонним каузальным оператором h(). Входной сигнал s(t) пропускается через систему в обычном порядке, и выполняется свертка g(t) = h()_*s(t). Затем выходной сигнал g(t) реверсируется (g(t)=>g(-t), конец сигнала становится его началом в порядке возрастания t) и повторно пропускается через систему, т.е. выполняется свертка y(-t) = h()_*g(-t) . Полученный сигнал снова реверсируется y(-t) => y(t), и результат является окончательным выходным сигналом y(t) системы.

Три последние операции (реверс g(t)  свертка c h()  реверс выходного сигнала) эквивалентны свертке сигнала g(t) с реверсированным откликом системы h(-), и сдвиг по фазе при свертке реверсированного сигнала компенсирует сдвиг по фазе сигнала, полученный при первой свертке. Общий результат операции y(t) = h()_*h(-)_*s(t) не имеет сдвига по фазе выходного сигнала относительно входного. Такую операцию приходится выполнять для исключения сдвига фазы при применении рекурсивных систем, которые всегда являются односторонними.

Рис. 3.3.4.

2. Второй способ. Выходной результат y(t) = h()_*h(-)_*s(t) предыдущей операции позволяет, используя свойство коммутативности свертки, сначала выполнить свертку h()_*h(-) = h() и получить один системный оператор h() (см. рис. 3.3.4), обеспечивающий свертку без сдвига фазы. Этот системный оператор является двусторонним и симметричным относительно  = 0. Но использование его возможно только для предварительно записанных сигналов, т.к. при выполнении свертки y(t)= h()_*s(t-) для отрицательных значений  требуются "будущие" значения входного сигнала s(t+). Результат свертки с симметричным оператором полностью аналогичен первой операции (сигнал y(t) на рис. 3.3.3).

На практике вполне естественным является расчет непосредственно симметричных двусторонних операторов под требуемые задачи обработки числовых данных (сигналов, зарегистрированных в дискретной числовой форме).

Начальные условия свертки. В начальный момент свертки, при вычислении значений y(t_i) для значений t_i < _max оператора h(), функция оператора, построенная в режиме обратного времени, при >t_i "зависает" для значений t_i- против отсутствующих значений входной функции.

Рис. 3.3.5.

Пример такого зависания оператора дискретной свертки против несуществующих отсчетов s_-1 и s_-2 входного массива данных при вычислении отсчета у₀ приведен на рис. 3.3.5. Зависание исключают либо заданием начальных условий - дополнительных отсчетов, чаще всего нулевых или равных первому отсчету входной функции, либо началом свертки с отсчета входной функции k_i = n_max с соответствующим сокращением интервала выходной функции на интервал задания системного оператора. Для симметричных операторов со значениями -n (вперед по времени) такой же момент наступает и в конце входного массива, и требует задания конечных условий или сокращения размера выходного сигнала.