2. Лекция 1.2. Пространство R3 (1 с.) +

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский государственный горный университет

Предмет:

Линейная алгебра

Файл:

x1 y1 x2 y2

.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

430.98 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ЛЕКЦИЯ 1.2

Трёхмерное евклидово пространство

Скалярное произведение векторов и его свойства, ортогональность.

Пусть в трёхмерном пространстве задана упорядоченная пара x, y векторов

e 1

e 2

x3 e 3 , y

e 1

e 2

e 3 .

Отображение x, y

: R3 R3 R , ставящее в соответствие каж-

дой упорядоченной паре трёхмерных (двумерных) векторов однозначно определённое действительное число, называется действительной функцией двух век-

торных переменных x и y .

Действительная функция двух векторных переменных, действие которой определяется правилом


называется скалярным произведением векторов x и				y .

Если x		y , то величина
		3	2
			2	(1.15')
x,	x	x1x1 x2 x2 x3 x3 xk		(1.15')
		r 1

Называется скалярным квадратом радиус-вектора x . Очевидно, что теперь мож-

но записать норму (длину) (1.1) радиус-вектора x в виде:

		def

				2		2	x3	2
	x			2		2		2			(1.16)
	x		x1		x2				x,	x .	(1.16)

Из определения (1.15) нетрудно получить следующие свойства скалярного
произведения:

1) x, y					y, x ;

				(1.17)
2) x, y	x, y	; x, y	x, y ;	(1.17)


3) x	y, z	x, z	y, z ;

			0 ,
4)	x	0 x, x	0 ,


x, y	z	x, y	x, z ;

где R . Рекомендуется провести вывод этих свойств скалярного произведения самостоятельно. Первое свойство выражает тот факт, что скалярное произведение симметрично относительно перестановки аргументов. Второе свойство означает, что скалярное произведение является однородным относительно каждого из своих аргументов. Третье свойство выражает факт того, что скалярное произведение аддитивно относительно каждого из своих аргументов. И, наконец, четвёртое свойство означает, что скалярное произведение невырождено.

Вектор, длина которого равна единице, называется нормированным. Каждый вектор можно нормировать, умножив его на нормирующий множитель

	1
	1

x		. Действительно, пусть x , R – вектор с длиной, равной 1 (его

скалярный квадрат, следовательно, также равен единице). Запишем скалярный


квадрат вектора x :

	x, x	2		1.
	x, x	2	x, x	1.

Откуда имеем:

2 1x, x

Здесь мы использовали определение (1.16) и свойства (1.17). Вектор

def

(1.18)

называется ортом вектора x .

Два вектора

x x1

e 1

e 2

e 3 , y

e 1

e 2

e 3 ,

называются ортогональными, если их скалярное произведение равно нулю:

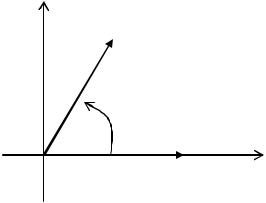
Теорема 1.1. Скалярное произведение векторов в трёхмерном (двумерном) пространстве равно произведению их норм (длин) на косинус угла между векторами

cos .

(1.20)

x, y

До к а з а т е л ь с т в о. Пусть x, y – данные ненулевые векторы, а –

угол между ними. Тогда по свойствам (1.17) имеем:


x y, x y					x, x	2 x, y			y, y .

C учётом (1.16) получаем:
		2		2				2
		2		2				2
	x y		x		2 x, y		y	.


Видим, что скалярное произведение векторов x, y выражается через их нор-

мы (длины) и, следовательно, не зависит от выбора системы координат.

Выберем декартову ортогональную систему координат, как показано на ри-

сунке 1.7 (ось OX 3 направлена перпендикулярно плоскости страницы). Тогда для координат векторов имеем:

; x2

0 ; x3 0; y1

cos ; y 2

sin ; y3

0 .

X 2

O		X 1
O	x

Рис. 1.7.

Подставляя выражения координат в (1.15), приходим к формуле (1.20):

cos .

x, y

cos 0

sin 0 0

Из теоремы виден смысл термина “ортогональность”: если векторы пер-

пендикулярны, то их скалярное произведение равно нулю так как cos

0 , то

есть векторы ортогональны.

Верно и обратное:

если скалярное произведение

векторов равно нулю (векторы ортогональны), то они перпендикулярны. Таким образом, ортогональность и перпендикулярность являются синонимами одного и того же свойства векторов.

Нетрудно видеть, что векторы канонического базиса (1.5) попарно орто-

гональны, что проверяется непосредственным вычислением. Кроме этого, векто-


		, e		, e				, x		, x
ры e	1	, e	2	, e	3	нормированы. Если векторы системы x	1	, x	2	, x	3 попарно

ортогональны (ортонормированны), то эта система называется ортогональной

(ортонормированной).

Любая ортогональная (ортонормированная) система векторов линейно


					,	x 2 ,	x
независима. Действительно, если система x				1	,	x 2 ,	x	3 ортогональна, то, на-

ходя скалярное произведение обеих частей векторного равенства

1 x1	2 x 2	3 x 3	0

последовательно на x1 , x 2 , x 3 , получаем

			0	,			0	,			0 .
	x1	, x1	0	,	x 2 , x	2	0	,	x 3 , x	3	0 .
1				2				3

Откуда имеем 1 2 3 0, что и доказывает линейную независимость

системы векторов.

Обычное трёхмерное пространство с введённой ортогональной декартовой системой координат является третьей степенью множества действительных

чисел R R R R3 , поэтому его обозначают R3 .

Определение 1.1. Множество трёхмерных векторов с определёнными выше внутренней бинарной (алгебраической) операцией – сложением векторов, внешней бинарной операцией – умножением вектора на число и заданной на нём функцией – скалярным произведением векторов, называется трёхмерным

евклидовым пространством R3 .

Измерения в пространстве R3 . По теореме 1.1 (формула (1.20))

cos		1
				x, y ,
				x, y ,

	x		y

Откуда с учётом формулы (1.7') получаем формулу для вычисления косинуса угла

между векторами в пространстве R3 :
cos	x1 y1 x2 y2 x3 y3
	x1 2 x2 2 x3 2	y1 2 y2 2 y3 2 .	(1.21)

Величина, определённая формулой

			x,		y	x y		1	x	2	y		2	x		3	y	3
			x,		y

						1
		cos
Pr x	x																		.	(1.22)

				y			y	y							y
y						1 2						2		2			3 2

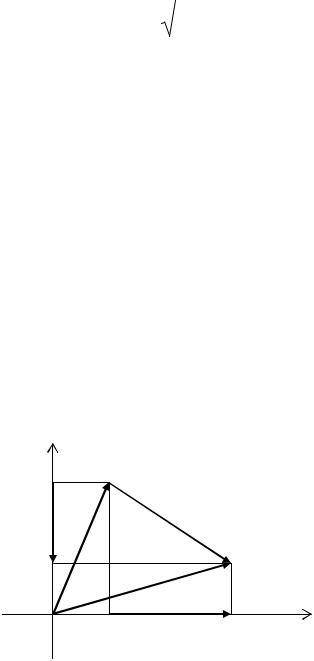
называется проекцией вектора x на направление вектора y .

До сих пор проводили все рассмотрения для радиус-векторов. Для опреде-

ления расстояния между точками пространства R3 нам потребуется понятие длины (нормы) произвольного вектора.

Рассмотрим, для простоты, двумерный случай (рисунок 1.6). По опреде-


лению, координатами	вектора	x	y , начальной		точкой которого				является

конечная точка вектора	y , а конечной точкой			– конец вектора x , называются
величины

z1 M ' N ' , z	2 M '' N ''



координатных проекций M ' N '		и M '' N '' вектора x				y .
	X 2	M
		M
	M ''

			x y
	y		x y
	y
	N ''			N
	N ''

			x
	O	M '		N '		X	1
							1

			Рис. 1.8.

Из рисунка 1.8 легко видеть, что координаты z1					и z 2		вектора x	y равны

z1 x1 y1 , z 2 x2 y2 .

Поэтому расстояние M , N между начальной точкой M вектора x

y и его

конечной точкой N равно длине вектора MN

x y и вычисляется по форму-

ле

M , N

x1 y1

2 x2 y 2 2 .

Очевидно, что в трёхмерном случае расстояние между двумя точками M и N

пространства R3 вычисляется по формуле

M , N

y2 2

x3 y3 2

(1.23)

где

x1 e1 x2 e 2

e 3 , y

y1 e1

y2 e 2

y3 e 3

– радиус-векторы точек N и M соответственно.

Векторное и смешанное произведения векторов. В трёхмерном евклидо-

вом пространстве кроме операции сложения векторов существует ещё одна алгебраическая операция – векторное умножение векторов, наличие которой превращает трёхмерное пространство в алгебру.

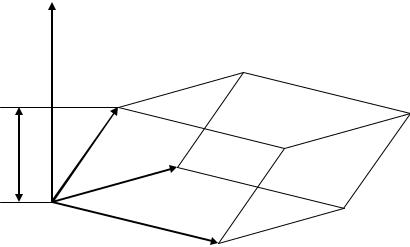
Определение 1.3. Тройка некомпланарных векторов x, y, z называет-

ся правой (левой), если эти векторы располагаются так, как могут быть расположены, соответственно, большой, не согнутые указательный и средний пальцы правой (левой) руки.


	y
O

	x
Рис. 1.9.

Например, тройка векторов x,	y, z на рис. 1.9 – правая. Из любых


трёх некомпланарных векторов x, y, z	можно составить шесть троек:


x, y, z , y, z , x , z, x, y ,



y, x, z , x, z, y , z, y, x .

Первые три тройки векторов того же наименования, что и тройка

x, y, z , то

есть правые, следующие три тройки – левые.

Определение 1.4. Декартова система координат называется правой (левой) системой координат, если тройка базисных векторов правая (левая).

Дальше рассматриваем исключительно правые системы координат.

Определение 1.5. Пусть дана упорядоченная пара векторов x, y . По-

ставим этим векторам в соответствие третий вектор z , потребовав выполнения условий:

вектор z ортогонален векторам x,

y ;

тройка векторов x,

y, z правая;

длина (норма)

вектора z численно равна площади

параллело-

грамма, построенного на приведённых к общему началу векторах

y (рисунок

1.10);

0 .

Если векторы x,

y коллинеарны, то полагаем

Построенное соответствие является алгебраической операцией над век-

торами в пространстве R3

и называется операцией

векторного умножения

вектора x на вектор y .

Вектор

z из определения 1.5 называется векторным произведением век-

тора x на вектор y . Для операции векторного умножения используется одно из следующих обозначений:

				8

z	x, y	x y	x y	x y .


		, e		, e
Пусть e	1	, e	2	, e	3 – базис декартовой системы координат, тогда по оп-

ределению 1.5 имеем:

1 , e

e 3

e 2 ;

1 , e 1

, e 1 , e

, e

e 3 ,

e 2

, e

e 2 ,

e 2

3 e 1;

(1.24)

, e

e 2

3 , e

e 1

3 , e

0 .

, e

Из (1.24) следует, что операция векторного умножения, являясь алгебраической, не является коммутативной. Иногда говорят, что операция вектор-

ного умножения векторов антикоммутативна.



x, y

		V
	z
h
h		y
		y
		S
	O

Рис. 1.10.

Как будет видно из дальнейшего изложения, операция векторного умножения векторов имеет большие приложения в геометрии. Однако приложениями в геометрии роль операции векторного умножения не исчерпывается – весьма широко данная операция применяется в теории поля.

Рассмотрим теперь функцию трёх векторных аргументов, определённую на


каждой тройке векторов трёхмерного пространства x,	y,	z , приложенных к

общей точке O . Такая тройка векторов определяет некоторый параллелепипед,

		9

объём которого обозначим V x, y,		z . Значение этой функции вычисляется в

соответствии со следующим определением.

Определение 1.6. Ориентированным объёмом V
Определение 1.6. Ориентированным объёмом V				x, y,	z параллеле-


пипеда, построенного на приведённых к общему началу векторах					x, y, z , назы-

вается его объём, взятый со знаком плюс, если тройка x, y, z					правая, и взя-


тый со знаком минус, если тройка векторов x, y,			z левая.

Определение 1.7. Если сначала производится векторное умножение век-

тора x на вектор	y , а затем вычисляется скалярное произведение вектора

x, y

шанным

	то полученное
на вектор z ,	то полученное	число x,	y ,	z называется сме-


произведением	векторов x,	y, z .

Теорема 1.2. Смешанное		произведение
Теорема 1.2. Смешанное		произведение	x,	y ,	z равно ориентиро-



ванному объёму V x,	y, z параллелепипеда, построенного на приведённых к


общему началу векторах x, y,		z .

Д о к а з а т е л ь с т в о. Пусть векторы x и y неколлинеарны. Обозначим

через S площадь параллелограмма, построенного на этих векторах. Тогда по определению скалярного произведения имеем:



x, y , z	x, y	z	cos x,

	S Pr
y , z	S Pr	z .
	x , y

		(1.25)

Если векторы x, y, z некомпланарны, проекция Pr
Если векторы x, y, z некомпланарны, проекция Pr	z	с точностью до
x , y

знака равна высоте h параллелепипеда, построенного на приведённых к общему

	10

началу	векторах x, y, z , причём основанием последнего служит параллело-

грамм,	построенный на векторах x, y (рисунок 1.10). Таким образом, правая

часть (1.25) есть с точностью до знака объём параллелепипеда, построенного на


векторах x, y, z . Когда Pr		h , векторы
векторах x, y, z . Когда Pr	z	h , векторы
x , y


x, y		и z лежат по од-

ну сторону от плоскости, образованной векторами x и y , и тройка векторов

торы x, y, z компланарны, то

лепипеда равен нулю.

Следствие из теоремы 1.2.

отношение:


Pr		0	и искомый объём паралле-
Pr	z	0	и искомый объём паралле-
x , y

Для любых векторов x, y, z справедливо со-

								(1.26)
	x, y ,		z x,		y,	z .

Д о к а з а т е л ь с т в о.						Из симметрии скалярного произведения имеем

x,		y, z		y, z		, x	.

Чтобы доказать справедливость равенства (1.26), достаточно показать, что

	x, y , z			y, z		, x	.


Но это очевидно, так как тройкам одного наименования x,	y,	z	и y,	z,	x

соответствует один параллелепипед.

Справедливо следующее, легко проверяемое утверждение.

Утверждение 1.1. Пусть a R3 – произвольный фиксированный вектор,

тогда если для двух векторов x и y выполнено условие

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Линейная алгебра

#
03.06.2015182.41 Кб161. Векторная алгебра.pdf
#
03.06.2015407.86 Кб141. Лекция 1.1. Пространство R3 (1 с.) +.pdf
#
03.06.2015324.25 Кб221. Множества, операции, отношения.pdf
#
03.06.2015437.4 Кб51. Понятие предела (1 с.) +.pdf
#
03.06.2015430.98 Кб132. Лекция 1.2. Пространство R3 (1 с.) +.pdf
#
03.06.2015373.84 Кб53. Лекция 2. Прямая и плоскость (1 с.) +.pdf
#
03.06.2015238.61 Кб193. Операторы и матрицы.pdf