3. Лекция 2. Прямая и плоскость (1 с.) +

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский государственный горный университет

Предмет:

Линейная алгебра

Файл:

В отношении нормального вектора плоскости

справедливо

В отношении нормального вектора плоскости

справедливо

.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

373.84 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ЛЕКЦИЯ 2

Прямая линия и плоскость в евклидовых пространствах R2 и R3

До сих пор понятия прямой линии и плоскости не были определены строго и рассматривались на интуитивном уровне. В этом параграфе понятия прямой линии и плоскости вводятся строго, но в простейшем случае евклидовых про-

странств R2 и R3 . Дальнейшее обобщение теории плоскостей на случай векторных пространств произвольной размерности (аффинных и евклидовых) будет подробно изложено ниже.

Уравнения прямой линии на плоскости R2 . В пространстве R2

зафик-

сируем некоторый канонический базис

O, e 1 , e

2 , то есть введём декартову

; x1 с известными

систему координат.

Каждые две точки

; x2

(фиксированными)

координатами

определяют

фиксированный

вектор

M 0 M1 . Если мы умножим данный вектор на некоторый параметр t , кото-

рый может принимать произвольные значения из множества действительных чисел, то есть t , , то получим ведущий вектор


M 0 M	t a ,
начальная точка которого фиксирована, а конечная точка M x1; x2		является

текущей, то есть имеет меняющиеся в зависимости от значения параметра t ко-

ординаты. Бесконечное множество текущих точек M x1; x2 назовём пря-

мой линией L , проходящей через точку M 0 x10 ; x02 и имеющей направляю-


щий вектор a	M 0 M1 .

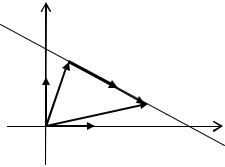
Получим уравнения для координат текущей точки M x1; x2 . Для этого

обратимся к рисунку 2.1. Из рисунка видно, что выполняются следующие соотношения:

OM 0

M 0 M

OM , M 0 M

t a ,

x1 e 1

2 , OM x1 e 1

e 2 , a

a1 e 1

e 2 .

Подставляя в первое соотношение все остальные, получаем следующее равенство


x1 e 1	x2 e 2	x1	e 1	x2	e		e 1 a2
x1 e 1	x2 e 2	x1	e 1	x2	e	2 t a1	e 1 a2
		0		0

e2 .

X 2

L		M 0
		M 0

e	2		M
e	2	a	M
		a
			X 1

O e1

Рис. 2.1.

Приравнивая координаты векторов в правой и в левой частях этого равенства, по-

лучаем параметрические уравнения прямой линии на плоскости R2 :

x1	x10	a1 t,
		(2.1)
x2	x02 a2 t.

Из параметрических уравнений (2.1) легко получить так называемые канонические уравнения прямой линии, для этого прибавляя к обеим частям первого

и второго уравнений соответственно x10 и x02 и деля обе части получившихся равенств на a1 и a2 соответственно, получаем следующие равенства:


		1		1
	x		x0		t,

			a	1

		2	x02
x					t.
			a	2

Приравнивая левые части, получаем следующие уравнения:

x1 x1	x2 x2
0	0	,	(2.2)
a1	a2	,	(2.2)
a1	a2

которые называются каноническими уравнениями прямой линии на плоскости

R2 .

Исключим из (2.1) параметр t , для чего умножим первое уравнение на a2 , а второе на a1 и, вычтем получившиеся равенства, получим

a2 x1 a1 x2 a2 x1				a1 x2		,
			0		0
или	a1	x2			0.
a2 x1 x1	a1	x2	x2		0.	(2.3)
0				0

Из этого равенства видно, что вектор

				a1
N		a2	e1	a1	e 2

							3

ортогонален направляющему вектору прямой линии a								M 0 M1 и текущему
вектору
			x1 x1		x2
M	0	M	x1 x1	e1	x2	x2	e 2 .
	0		0			0

Вектор N называется нормальным вектором прямой линии L . Теперь очевид-

но, что уравнения прямой линии (2.1) эквивалентны условию ортогональности


нормального вектора прямой линии N и текущего вектора M 0 M , то есть

N, M 0 M 0 .

Обозначая a2 A, a1 B и		a2 x1	a1 x2	C , получаем неявное
		0	0
уравнение прямой линии, записанное в стандартной форме
A x1	B x2 C 0,			(2.4)

которое иногда называют общим уравнением прямой линии. Из уравнения (2.4) при условии C 0 получаем уравнение прямой линии в отрезках


	x1		x2			1,		(2.5)
	a		b

где a		C		,	b		C	. Условие C 0 , очевидно, означает, что прямая линия не
							B
		A

проходит через начало координат. Геометрический смысл коэффициентов a и b легко выясняется из рисунка 2.1 – эти коэффициенты равны, соответственно, ве-

личинам отрезков, отсекаемых прямой линией L на осях координат.

Заметим, что, так как мы рассматриваем свободные векторы, для подсчёта координат которых положение начала системы координат не имеет значения, в качестве направляющего вектора мы можем при выводе параметрических уравне-

ний прямой линии выбрать любой вектор a , коллинеарный любому вектору, лежащему на прямой L . Аналогично, в качестве нормального вектора мы можем выбрать любой вектор, ортогональный любому вектору, лежащему на прямой L .

Пример 2.1. Получить уравнение прямой линии L , проходящей через точ-


ку M0 3; 2 и имеющий нормальный вектор N		e1	4 e 2 .

Р е ш е н и е. Уравнение прямой линии получается из условия ортогональ-

ности вектора N и ведущего вектора прямой линии

		x2
M0M	x1 3 e1	x2	2 e 2 ,

то есть

N, M 0 M 0.

Используя выражение для скалярного произведения

4 x2 5,

N, M

M x1

получаем неявное уравнение прямой линии x1 4 x2

5 0 .

Уравнение прямой линии в трёхмерном пространстве R3 . Рассмотрим

теперь

случай

пространства R3 (рисунок 2.2). Очевидно, что справедливы

следующие соотношения:

OM ,

M t a ,

e 1 x2

e 2 x3 e 3 ,

e 1

2 e 2

x3 e 3 ,

a a1 e1 a2 e 2 a

3 e 3 ,

которые отличаются от соответствующих соотношений для плоскости R2

только

наличием третьей координаты.

X 3

M 0

X 1

Рис. 2.2.

Поэтому, простые преобразования дают

x1 e1 x2 e 2 x3 e 3

e1 x2 e 2

a2 e 2

a3 e

x3 e 3 t a1

3 ,

откуда следуют параметрические уравнения прямой линии в пространстве

R3 :

x1		x10
		x02
x2		x02
	3	3
x		x0

a1 t,

a2	t,	(2.6)
a3	t.

Из уравнений (2.6) нетрудно получить канонические уравнения прямой линии в пространстве R3 , которые имеют вид:

x1 x10	x2 x02	x3 x03	.	(2.7)
a1	a2
		a3

В параграфе 2.10 (задача 2.10.3) показано, что канонические уравнения прямой линии (2.7) выражают тот факт, что прямая линия является множеством точек пе-

ресечения двух плоскостей в пространстве R3 .

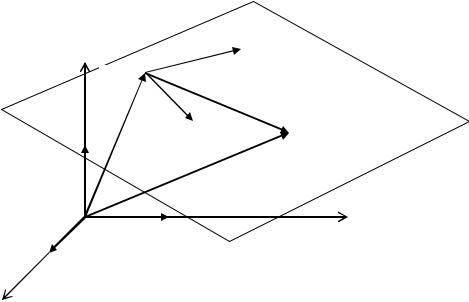
Уравнения плоскости в пространстве R3 . На рисунке 2.3 изображена

фиксированная точка M 0 , от которой откладывается вектор M 0 M , который яв-

ляется вектором из линейной оболочки неколлинеарных векторов a 1 и a 2 , закреплённых в точке M 0 .

X 3
		a 2
M 0

x 0		M
	a	M
	a	1

e 3
e 3		x
		x
O
		X	2
e	2	X
e	2

e1
		Рис. 2.3.

X 1

Непосредственно из рисунка видно, что выполняются следующие соотношения:

OM 0

M 0 M

OM ;

M0M t1 a1 t2 a 2 ;

x 0

e 1

2 x3

3 ;

x OM x1

e 1 x2

e 2 x3

e 3 ;

e 1 a2

e 2 a3

e 3 ;

a 2

e 1

e 2

3 .

Истолковывая первое из приведённых соотношений аналогично тому, как это было сделано при выводе уравнения прямой линии, и записывая его с учётом второго соотношения в виде


x	x 0 t1 a1 t2 a 2 ,					(2.8)
приходим к понятию плоскости.
Назовём		плоскостью H 2			в пространстве R3 множество текущих
точек M x1;		x2 ; x3	, являющихся конечными точками вектора

M0M t1 a1			t2	a 2 ,

							, a
представленного разложением по паре неколлинеарных векторов a1							, a	2 ,

приложенных к точке				M 0 x10 ; x02 ; x03 , при всевозможных значениях пара-

метров t1 и					a
метров t1 и		t2 . Векторы a1 ,			a	2 называются направляющими векторами

плоскости H 2 .

Само уравнение (2.8) называется векторным параметрическим уравнением плоскости.

Подстановка всех соотношений

в векторное уравнение плоскости даёт:

x1 e1

x2 e 2

x3 e 3

2 x3

e1 a2

e 2 a3

e1 a2

e 2

t a1

3 .

Из последнего равенства получаем параметрические уравнения плоскости H 2 в евклидовом пространстве R3 :

x1x2

x10

x02

x03

a11 t1 a12

a12 t1 a22

a13 t1 a23

t2 ,

t2 , (2.9)

t2 .

Рассмотрим следующее преобразование уравнений (2.9). Исключим пара-

метры t1	и t2 из системы уравнений (2.9), для чего рассмотрим первые два
уравнения как систему относительно параметров
1	1	1	1
a1	t1 a2 t2 x		x0 ,

a12 t1 a22 t2 x2 x02 .

Предполагая, что a11 a22 a12 a12 0 (условие, следующее из того, что направ-

ляющие векторы линейно независимы), решим систему, умножая обе части каждого из уравнений на соответствующие величины и складывая уравнения почленно:

x2 x2

2 a1

x1 x1

0 2

0 2 , t

0 1

1 .

Подстановка в третье уравнение системы (2.9) после простых преобразований приводит нас к следующему равенству

a3	a2	a3	a2 x1		a3 a1 a3					a1 x2				a1	a2		a2	a1 x3
2	1	1		2			1	2	2		1			1		2	1		2	x3
a3 a2 a3				a2 x1			a3	a1	a3		a1 x2			a1		a2 a2			a1	x3		,
	2	1	1	2	0		1	2		2		1	0		1		2	1	2		0
																		(2.10)
которое может быть переписано в виде													x2 x2
a3	a2	a3 a2 x1			x1		a3 a1			a3		a1	x2 x2
2	1	1		2		0		1	2		2	1				0
a1 a2 a2 a1 x3						x3		0 .
	1	2	1	2			0

Из этого равенства видно, что скалярное произведение векторного произведения


		,	a 2
a1		,	a 2

a3															a1
a3			a2			a3 a2			e1 a3 a1		a3 a1		e	2	a1	a2	a2	a1	e 3
		2		1			1	2	1	2	2	1			1	2	1	2

на текущий вектор M 0 M равно нулю. Поэтому вектор


N a				1 , a			2

естественно назвать нормальным вектором плоскости																H 2	в пространстве
R3 . Соотношение (2.10) можно переписать в виде

	a1 , a				2 ,		OM		a1 , a	2 , OM 0		,							(2.11)

из которого видно, что из параметрических уравнений плоскости (2.9) следует по-

стоянство ориентированного объёма параллелепипеда, построенного на приведённых к общему началу направляющих векторах и радиус-вектора теку-


щей точки плоскости. Обозначая в (2.10) координаты вектора		1 , a		соот-
	a		2

ветственно	A , B и C , а правую часть D , получаем неявное уравнение плос-
кости
A x1	B x2 C x3 D 0.	(2.12)

Из уравнения (2.12) при условии D 0 получаем уравнение плоскости в

отрезках

x1	x2	x3	1,	(2.13)
a	b	c

где a DA , b DB , c CD . Нетрудно видеть, что эти коэффициенты равны

величинам отрезков, отсекаемых плоскостью на осях координат. Очевидно, что уравнение плоскости в отрезках может быть получено только в том случае, если плоскость не проходит через начало координат.

то же замечание, что и в отношении нормального вектора прямой линии на плос-

кости R2 : в качестве нормального вектора можно выбрать любой вектор, ортогональный произвольному вектору, лежащему в плоскости.

Взаимное расположение прямой линии и плоскости в пространстве R3 .

Среди различных задач, решаемых средствами аналитической геометрии в про-

странстве R3 , есть несколько типичных, а именно: задача определения двугранного угла между плоскостями; задача получения уравнения прямой линии, заданной как пересечение двух плоскостей; задача определения координат точки пере-

сечения прямой линии L и плоскости H 2 ; задача определения координат проекции точки M 0 x10 ; x02 ; x03 на плоскость H 2 и расстояния от данной точки до плоскости. Рассмотрим решение этих задач последовательно.

Угол между плоскостями H 2 и H 2 . Пусть требуется найти угол между

1 2

плоскостями, проходящими через три, не лежащие на одной прямой точки

A1 x11; x12 , x13 , A2 x12 ; x22 , x23 , A3 x31 ; x32 , x33 ,

B1 y11; y12 , y13 , B2 y12 ; y22 , y23 , B1 y31 ; y32 , y33 ,

соответственно. Для решения этой задачи поступаем следующим образом: 1) за направляющие векторы плоскостей принимаем векторы


a1	A A		a1		e 1	a2		e	2	a3		e	3 ,
	1	2	1			1					1

a 2	A A		a1		e 1 a2			e		2 a3 e 3 ;
	1	3	2			2					2

b1	B B		b1		e 1	b2	e		2	b3		e	3 ,
	1	2	1			1					1

b 2	B B		b1	e1 b2 e 2					b3		e 3
	1	3	2			2				2

соответственно.

2) находим нормальные векторы плоскостей как векторные произведения направляющих векторов:

N 1 A1 A2 , A1 A3 ,

N 2

B1B2 , B1B3

;

3) находим косинус угла между плоскостями, как косинус угла между

нормальными векторами плоскостей:

N 1 , N 2

cos

N 1

N 2

Если плоскости заданы своими параметрическими уравнениями

x10 a11 t1

a12 t2

x10 b11 s1 b21 s2 ,

x02

a12 t1

a22 t2 ,

x02 b12 s1 b22 s2 ,

a3 t a3 t

s b3 s

где M

x1 , x2

, x3 и

, y2 , y

–

точки,

через

которые проходят

плоскости, а

i 1, 2, 3;

j 1, 2 и

i 1, 2, 3; j 1, 2 – координаты

направляющих векторов плоскостей, то находим направляющие векторы из параметрических уравнений. Далее, находим угол через его косинус.

Если плоскости заданы неявными уравнениями

x2 C

x3 D

0 ;

x2 C

x3 D

0 ,

то, учитывая,

что

координаты

нормальных

векторов

равны

соответственно

A 1 , B 1 , C 1 и A 2 , B 2 , C 2 , угол между плоскостями находим из соотно-

шения

A 1 A 2

B 1 B 2 C 1 C 2

cos

A 2

B 2

C 2

2 B 2

Уравнение прямой линии, заданной пересечением двух плоскостей.

Пусть требуется найти параметрические или канонические уравнения прямой линии, заданной как множество точек пересечения двух плоскостей с неявными уравнениями:

A 1 x1 B 1 x2 C 1 x3 D 1 0 , A 2 x1 B 2 x2 C 2 x3 D 2 0 .

1. Проверяем, что плоскости пересекаются, то есть, что нормальные векторы неколлинеарны. Ищем направляющий вектор прямой линии и какуюлибо её точку.

2. Так как плоскости пересекаются по прямой, то её направляющий вектор ортогонален нормальным векторам обеих плоскостей. Поэтому



			e 1	e 2	e 3

a	N	1 , N 2	A	B	C	1	.
			1	1		1
			A 2	B 2	C 2
			A 2	B 2	C 2

3. Так как направляющий вектор прямой линии непарралелен хотя бы одной из координатных плоскостей, то в качестве точки на прямой линии выбираем точку пересечения этой прямой и координатной плоскости.

4. Подставляя координаты точки прямой и направляющего вектора в параметрические или канонические уравнения прямой, получаем ответ.

Координаты точки пересечения прямой линии

L и плоскости

H 2 .

Пусть требуется

найти координаты точки пересечения прямой

линии

L и

плоскости H 2 , заданных соответственно уравнениями

x1 x10

x2 x02

x3 x03

, A x1 B x2 C x3

D 0 .

Для решения этой задачи поступаем так.

1. Проверяем, что прямая линия не параллельна плоскости, то есть, что

направляющий вектор прямой

a a1 e 1

a2 e 2

a3 e 3

не ортогонален нормальному вектору плоскости N A e 1 B e 2

C e 3 :

a, N A a1 B a2 C a3 0 .

2. Параметрические уравнения прямой линии имеют вид

x10 a1 t,

x02 a 2 t,

x0 a

Подставляя эти выражения для координат точек прямой x1 , x2 , x3 в неявное уравнение плоскости, получаем уравнение относительно параметра t , решая которое, находим значение парамтра t t0 , при котором происходит пересечение прямой линии и плоскости.

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Линейная алгебра

#
03.06.2015182.41 Кб161. Векторная алгебра.pdf
#
03.06.2015407.86 Кб141. Лекция 1.1. Пространство R3 (1 с.) +.pdf
#
03.06.2015324.25 Кб221. Множества, операции, отношения.pdf
#
03.06.2015437.4 Кб51. Понятие предела (1 с.) +.pdf
#
03.06.2015430.98 Кб132. Лекция 1.2. Пространство R3 (1 с.) +.pdf
#
03.06.2015373.84 Кб53. Лекция 2. Прямая и плоскость (1 с.) +.pdf
#
03.06.2015238.61 Кб193. Операторы и матрицы.pdf