
Лекция 3 +
.doc
Элементарная теория вероятностей
ЛЕКЦИЯ 3
Понятие случайной величины. Современная теория вероятностей оперирует случайными величинами, а не событиями. Так намного удобнее. Дадим определение случайной величины.
Определение
3.1. Случайной
величиной
называется переменная величина, которая
в результате опыта может принять одно
из возможных значений, причём заранее
не известно какое именно.![]()
Пример 3.1. 1) Число очков, выпавших при однократном бросании игральной кости есть случайная величина, которая может принять одно из возможных значений: 1, 2, 3, 4, 5, 6.
2) Число мальчиков среди пяти новорожденных есть случайная величина, которая может принять одно из возможных значений: 0, 1, 2, 3, 4, 5.
3) Число попаданий в мишень при трёх выстрелах есть случайная величина, которая может принять одно из возможных значений: 0, 1, 2, 3.
4)
Количество осадков, выпавших в данной
местности, в данном месяце есть случайная
величина, которая может принять одно
из возможных значений из некоторого
промежутка
![]() ,
где
,
где
![]() – величина уровня осадков, например, в
миллиметрах.
– величина уровня осадков, например, в
миллиметрах.
5)
Расстояние между эпицентром взрыва
бомбы и целью, на которую она сброшена,
есть случайная величина, которая может
принять любое неотрицательное значение.
![]()
В примерах 1 – 3 множество значений случайной величины состоит из изолированных элементов, которые можно перечислить.
Определение
3.2. Случайная
величина, множество значений которой
либо конечно, либо счётно, называется
дискретной
случайной величиной.![]()
В примерах 4 и 5 допустимые значения случайной величины непрерывно заполняют некоторый промежуток числовой оси, который иногда замкнут, а иногда нет.
Определение
3.3. Случайная
величина, множество значений которой
является промежутком действительной
числовой оси, называется непрерывной
случайной величиной.
![]()
Определение
3.4. Пусть
производится эксперимент, в результате
которого может появиться или не появиться
некоторое событие
![]() .
Случайная величина
.
Случайная величина
![]()
называется
характеристической
случайной величиной события
![]() .
.
![]()
Если проводится
серия испытаний, в каждом из которых
может произойти событие
![]() ,
то общее число появлений этого
события равно сумме характеристических
функций случайных величин события
,
то общее число появлений этого
события равно сумме характеристических
функций случайных величин события
![]() во всех испытаниях.
во всех испытаниях.
Пример
3.2. Пусть
производится бомбометание, цель которого
– поражение некоторого объекта
![]() .
При бомбометании бомбы падают, рассеиваясь
случайным образом, по некоторой площади
в окрестности объекта. Рассмотрим
событие
.
При бомбометании бомбы падают, рассеиваясь
случайным образом, по некоторой площади
в окрестности объекта. Рассмотрим
событие
![]() ,
,
где
![]() – радиус рассеяния, при котором объект
поражается (рисунок 3.1). Если
– радиус рассеяния, при котором объект
поражается (рисунок 3.1). Если
![]() и
и
![]() – случайные координаты падения бомбы,
то появление события
– случайные координаты падения бомбы,
то появление события
![]() равносильно попаданию точки
равносильно попаданию точки
![]() в круг с радиусом
в круг с радиусом
![]() и с центром в точке
и с центром в точке
![]() (объект считается точечным). То есть,
для появления события
(объект считается точечным). То есть,
для появления события
![]() должно выполняться условие
должно выполняться условие
![]() .
.
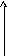
![]()

![]()

![]()
![]()
![]()
Рис. 3.1.
Вероятность
события
![]() есть вероятность выполнения неравенства
есть вероятность выполнения неравенства
![]() ,
,
которую
можно подсчитать, если известны свойства
случайных величин
![]() и
и
![]() .
.![]()
Дискретные
и непрерывные случайные величины будут
дальше обозначаться, соответственно,
большими буквами греческого и латинского
алфавита, а их значения – соответствующими
малыми буквами. Например, если
![]() – число попаданий по мишени в серии из
трёх выстрелов, то возможные значения
– число попаданий по мишени в серии из
трёх выстрелов, то возможные значения
![]() есть
есть
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Функция
распределения случайной величины.
Рассмотрим, сначала, дискретную случайную
величину
![]() ,
множество значений которой конечно.
Пусть эта случайная величина имеет
возможные значения
,
множество значений которой конечно.
Пусть эта случайная величина имеет
возможные значения
![]()
![]() ,
которые принимаются ею с некоторыми
вероятностями. Следовательно, в результате
опыта обязательно произойдёт одно из
элементарных событий
,
которые принимаются ею с некоторыми
вероятностями. Следовательно, в результате
опыта обязательно произойдёт одно из
элементарных событий
![]() .
Соответствующие этим событиям вероятности
обозначим
.
Соответствующие этим событиям вероятности
обозначим
![]() .
.
Так
как события образуют полную группу, то
сумма их вероятностей
![]() .
Эта суммарная вероятность как-то
распределена между событиями
.
Эта суммарная вероятность как-то
распределена между событиями
![]()
![]() .
Дискретная случайная величина
.
Дискретная случайная величина
![]() считается полностью описанной со
статистической точки зрения, если
указано, какой вероятностью обладает
каждое из этих событий.
считается полностью описанной со
статистической точки зрения, если
указано, какой вероятностью обладает
каждое из этих событий.
Определение
3.5. Соотношение,
устанавливающее связь между возможными
значениями
![]()
![]() дискретной случайной величины
дискретной случайной величины
![]() и соответствующими им вероятностями
и соответствующими им вероятностями
![]() ,
называется законом
распределения
дискретной случайной величины
,
называется законом
распределения
дискретной случайной величины
![]() .
.![]()
Простейшей
формой задания закона распределения
дискретной случайной величины является
ряд
распределения
дискретной случайной величины
![]() – таблица
следующего вида:
– таблица
следующего вида:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р яд
распределения иногда удобно изобразить
графически в виде так называемого
многоугольника
распределения
(рисунок 3.2).
яд
распределения иногда удобно изобразить
графически в виде так называемого
многоугольника
распределения
(рисунок 3.2).

![]()
![]()


![]()














![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 3.2.
Пример
3.3. В денежной
лотерее разыгрывается 1 выигрыш в 1000
руб., 10 выигрышей по 100 руб. и 100 выигрышей
по 1 руб. Общее число билетов 10000. Найти
закон распределения случайного выигрыша
![]() для владельца одного билета.
для владельца одного билета.
Р
е ш е н и е. Возможные значения дискретной
случайной величины
![]() есть
есть
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Соответствующие вероятности
.
Соответствующие вероятности
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Теперь закон распределения выигрыша может быть представлен в виде следующей таблицы
|
|
0 |
1 |
100 |
1000 |
|
|
0,9889 |
0,01 |
0,001 |
0,0001 |
Можно построить
многоугольник распределения этой
случайной величины.
![]()
Ряд распределения, однако, можно построить не всегда. Например, для непрерывной случайной величины, принимающей значения, заполняющие континуальное множество – некоторый открытый промежуток числовой оси, указать все её значения, очевидно, невозможно. Кроме того, ниже будет показано, что отдельное значение непрерывной случайной величины не обладает отличной от нуля вероятностью.
Рассмотрим общий способ описания распределения вероятности, справедливый как для дискретных, так и для непрерывных случайных величин.
Пусть
![]() – некоторая случайная величина.
Рассмотрим событие
– некоторая случайная величина.
Рассмотрим событие
![]() ,
где
,
где
![]() – некоторый порог
на действительной оси, причём
– некоторый порог
на действительной оси, причём
![]() может изменяться непрерывно. Множество
значений случайной величины
может изменяться непрерывно. Множество
значений случайной величины
![]() делится на два промежутка:
делится на два промежутка:
![]() и
и
![]() .
Вероятность
события
.
Вероятность
события
![]() является функцией от порога
является функцией от порога
![]() :
:
![]() .
.
Пусть
![]() – возможное значение случайной величины
– возможное значение случайной величины
![]() ,
принимаемое ею в эксперименте.
,
принимаемое ею в эксперименте.
Определение 3.6. Функция
![]() ,
(3.1)
,
(3.1)
показывающая,
как зависит от выбранного порога
![]() вероятность того, что значения случайной
величины
вероятность того, что значения случайной
величины
![]() не превосходят его, называется функцией
распределения (ФР)
вероятностей случайной
величины
не превосходят его, называется функцией
распределения (ФР)
вероятностей случайной
величины
![]() .
.![]()
Функция
![]() называется, также, интегральной
функцией распределения
или интегральным
законом распределения
случайной величины.
называется, также, интегральной
функцией распределения
или интегральным
законом распределения
случайной величины.
Функция распределения является универсальной характеристикой случайной величины. Она существует как для дискретных, так и для непрерывных случайных величин. Перечислим почти очевидные свойства функции распределения случайной величины.
Свойство 1.
Множеством
значений функции распределения
![]() случайной величины
случайной величины
![]() является замкнутый промежуток
является замкнутый промежуток
![]() .
.
Д о к а з а т е л ь
с т в о. Очевидно, в силу свойств
вероятности.![]()
Свойство 2. Предельное значение на «минус бесконечности» функции распределения равно нулю:
![]() .
(3.2)
.
(3.2)
Д
о к а з а т е л ь с т в о. Событие
![]() является невозможным событием.
является невозможным событием.
![]()
Свойство 3. Предельное значение на «плюс бесконечности» функции распределения равно 1:
![]() .
(3.3)
.
(3.3)
Д
о к а з а т е л ь с т в о. Событие
![]() является достоверным событием.
является достоверным событием.
![]()
Свойство
4. При
![]() вероятность того, что случайная величина
вероятность того, что случайная величина
![]() примет значение, заключённое в промежутке
примет значение, заключённое в промежутке
![]() ,
равна разности значений функции
распределения на верхнем и нижнем
порогах:
,
равна разности значений функции
распределения на верхнем и нижнем
порогах:
![]() .
(3.4)
.
(3.4)
Д о к а з а т е л ь с т в о. Рассмотрим три события:
![]() ,
,
![]() ,
,
![]() .
.
Очевидно, что
![]() ,
,
![]() .
.
Следовательно
![]() .
.
Используя определение (3.1), получаем
![]() ,
,
что
и требовалось доказать.
![]()
Свойство 5. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю:
![]() .
(3.5)
.
(3.5)
Д
о к а з а т е л ь с т в о. Воспользуемся
формулой (3.4). Будем неограниченно
уменьшать промежуток
![]() ,
полагая, что
,
полагая, что
![]() .
В пределе вместо вероятности попадания
случайной величины
.
В пределе вместо вероятности попадания
случайной величины
![]() в промежуток
в промежуток
![]() получим вероятность того, что случайная
величина
получим вероятность того, что случайная
величина
![]() примет одно (отдельное) значение:
примет одно (отдельное) значение:
![]() .
.
Если
функция
![]() непрерывна на промежутке
непрерывна на промежутке
![]() ,
то этот предел равен
,
то этот предел равен
![]() ,
,
что
и требовалось доказать.![]()
Свойство 5 кажется
парадоксальным. Однако парадокс
разрешается просто, если учесть, что
равенство (3.5) имеет предельный характер.
Действительно, предельный характер
равенства (3.5) означает только то, что
вероятность события
![]() исчезающе
мала.
Аналогию можно найти в следующем примере:
некоторое тело конечных размеров имеет
конечную массу, а масса любой его
бесконечно малой частицы стремится к
нулю.
исчезающе
мала.
Аналогию можно найти в следующем примере:
некоторое тело конечных размеров имеет
конечную массу, а масса любой его
бесконечно малой частицы стремится к
нулю.
С л е д с т в и е и з с в о й с т в а 5. Вероятность попадания непрерывной случайной величины в открытый промежуток, в замкнутый промежуток и полузамкнутые промежутки с одними и теми же граничными точками одинаковы:
![]()
(3.6)
Свойство
6. Функция
распределения
![]() есть неубывающая функция своего аргумента
есть неубывающая функция своего аргумента
![]() ,
то есть при любых
,
то есть при любых
![]()
![]() .
(3.7)
.
(3.7)
Д
о к а з а т е л ь с т в о. Так как в (3.4) левая
часть (как вероятность) неотрицательна
![]() ,
то правая часть также неотрицательна:
,
то правая часть также неотрицательна:
![]() .
Последнее и означает, что при
.
Последнее и означает, что при
![]() функция распределения
функция распределения
![]() неубывающая.
неубывающая.
![]()
Функция
распределения дискретной случайной
величины.
Для дискретной случайной величины
![]() функция распределения (ФР) имеет вид
функция распределения (ФР) имеет вид
![]() ,
(3.8)
,
(3.8)
где
учтено, что события
![]() несовместимы. Неравенство
несовместимы. Неравенство
![]() под знаком суммы означает, что суммирование
распространяется на все значения
под знаком суммы означает, что суммирование
распространяется на все значения
![]() ,
меньшие или равные
,
меньшие или равные
![]() .
Введём функцию единичного
скачка
.
Введём функцию единичного
скачка
![]() (3.9)
(3.9)
С помощью (3.9) можем записать (3.8) в виде
![]() .
(3.10)
.
(3.10)
Зная
функцию распределения дискретной
случайной величины
![]() ,
можно найти вероятности её отдельных
значений. Действительно, при
,
можно найти вероятности её отдельных
значений. Действительно, при
![]()
![]() .
(3.11)
.
(3.11)
Из
(3.7) или (3.8) легко видеть, что ФР дискретной
случайной величины
![]() является ступенчатой
функцией,
значения которой, вообще говоря,
начинаются от 0 и доходят до 1.
является ступенчатой
функцией,
значения которой, вообще говоря,
начинаются от 0 и доходят до 1.
Из
рисунка 3.3 видно, что величины пороговых
скачков функции распределения в точках
![]() равны соответствующим вероятностям
равны соответствующим вероятностям
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]()


![]()
![]()


![]()


![]()



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
