10. Неэмпирическая квантовая химия. Базисные функции для неэмпирических расчетов Вид аналитических базисных функций

Приближение MO ЛКАО - аппроксимация МО суммой AO, центрированных на всех ядрах (12). AO - решения уравнений ХФ для атома, т. е. одноэлектронные атомные волновые функции. Использование аналитических АО значительно упрощает вычисления.

Угловые части АО - сферические гармоники . Рассмотрим аналитические приближения к радиальным частям AO: именно они обычно определяют тип базиса.

Орбитали слейтеровского типа (STO или ОСТ) отвечают потенциалу центрального поля

V( r ) = - n/r + [n(n-1) –l(l+1)]/2r² (43)

(n и l - главное и орбитальное квантовые числа, l=0, 1, 2,… n-1) и удовлетворяют асимптотическому поведению точной волновой функции как вблизи ядра, так и на больших расстояниях от него. В сферических координатах ОСТ имеют вид:

_, (44)

N

Рис. 9. Радиальные части волновых функций 3d АО железа:

ХФ – хартри-фоковская АО;

DZ – двухэкспоненциальная ОСТ;

S- одноэкспоненциальная ОСТ.

– нормировочный множитель,- орбитальная экспонента.ОСТ сl > 1 безузловые; ОСТ с одинаковыми l, но разными n, неортогональны.

Орбитали гауссового типа (GTO или ОГТ) отвечают потенциалу центрального поля

V( r ) = 2a²/r²+ [n(n-1) – l(l+1)]/2r². (45)

О

G3

ГТ на данном центре с одинаковымиl, но разными n, как и ОСТ, не ортогональны. ОГТ обладают следующим важным свойством: произведение двух гауссиан, центрированных в точках А(А_x, А_y, А_z) и В ( В_x, В_y, В_z ), есть гауссиан, центрированный в точке P =(a₁A + a₂B) / (a₁+a₂), лежащей на линии АВ:

exp(-a₁r_A²) exp(-a₂r_B²)= exp[-(a₁a₂r_AB²)/( a₁+a₂)] exp[(-a₁+a₂)r_p²)]. (46)

нальны.

Р

G1

G2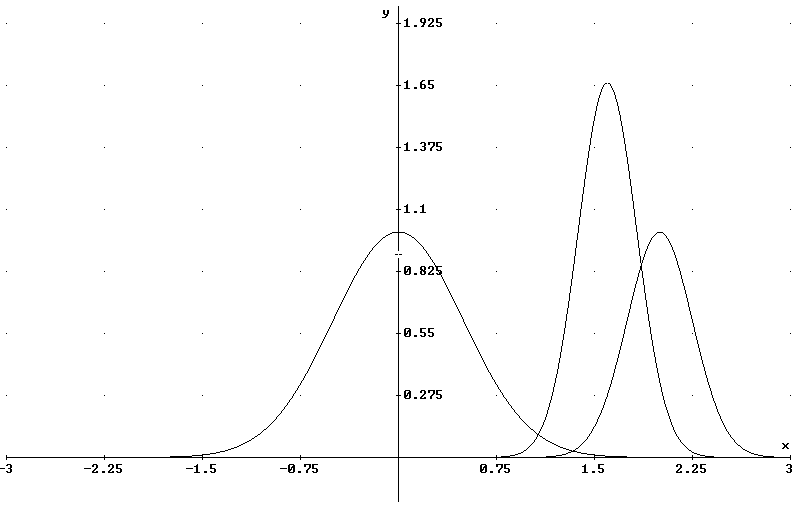

ис. 10. Произведение двух гауссианG1 = exp(-2x²) (с центром в точке А) и G2 = exp(-8(x-2)²) (с центром в точке В) есть третий гауссиан G3 = exp(-10x² +32x-32), центрированный в точке Р. Значение G3 умножено на 1000 для приведения в соответствие амплитуд гауссиан при их изображении.

Комбинации гауссиан = с_iG_i хорошо аппроксимируют основные свойства ХФ АО, если коэффициенты с_i имеют разные знаки. В квантово-химических расчетах используются, как правило, базисные наборы из декартовых ОГT (гауссовых примитивов), которые имеют вид

, (47)

N - нормировочный множитель, r²= x²+ y²+ z², сумма n+l+m, аналогично орбитальному квантовому числу для атомов, определяет вид угловой части ОГТ в декартовых координатах:

n+l+m =0 - s-тип, n+l+m =1 - p-тип , n+l+m =2 - d-тип , n+l+m =3 - f-типа и т.д.

Основные декартовы ОГТ:

1s = 3d_xx = x² 4f_xxx = x³

2p_x = x 3d_xy = x y 4f_xxy = x² y

2p_y = y 3d_xz = x z 4f_xyz = x y z

2p_z = z 3d_yy = y² и т.д. (48)

3d_yz = y z

3d_zz = z²

Сейчас базисные наборы строят из линейных комбинаций ОГT или из сгруппированных (или контрактированных) ОГT (CGTO или СОГТ): g_i=а_ijG_j. Термин «группировка» (контрактация, сжатие) означает, что линейные комбинации ОГТ G_j, с фиксированными коэффициентами а_ij и экспоненциальными множителями_ijиспользуются как базисные функция, т.е.=с_ig_i. Контрактация уменьшает время вычисления интегралов.

Номенклатура базисных наборов

На первых порах СОГТ получали методом наименьших квадратов подгонкой под единственную ОСТ с =1.0. Затем экспоненты в ОГТ умножали на² из радиальной части ОСТ (39), причем величина выбиралась так, чтобы наиболее подходить для данной молекулы. Соответствующие базисы обозначают STO-nG, где n - число примитивов в СОГТ.