Энергии реакций изомеризации (ккал/моль)

соединение	реакция	расчетн. энергия HF/6-31G* // 3-21G	эксперимент. значение энергии
HCN	цианид водорода  изоцианид водорода	12.4	14.5
CH2O	формальдегид  гидроксиметилен	52.6	54.9
CH3NO	формамид  нитрозометан	65.3	62.4
C2H3N	ацетонитрил  метил изоцианид	20.8	20.9
C2H4O	ацетальдегид  оксицианопропан	33.4	26.2
C3H6	пропен  циклопропен	8.2	6.9

Молекулярная структура есть совокупность конформаций молекулы в определенной структурной области, каждая из которых обладает определенной электронной конфигурацией и распределением электронной плотности.

2. Метод Хартри-Фока для молекул

Чтобы получить решение электронного уравнения Шредингера (4) для многоэлектронной молекулы при фиксированной ядерной конфигурации используют одноэлектронное приближение, приближение самосогласованного поля (ССП) и однодетерминантное приближение. Они приводят к методу Хартри-Фока (ХФ), уравнения которого имеют вид

(10)

В методе ХФ применительно к молекулам детерминант Слейтера-приближение к N-электронной волновой функции - составляется из занятых электронами молекулярных орбиталей (МО) _i(x):

. (11)

Молекулярная спин-орбиталь зависит от координат лишь одного электрона (является одноэлектронной) и записывается в виде произведения пространственной _i(x) и спиновой (s) компонент: _i(x)= _i(x)(s). Каждая МО характеризуется своим значением энергии _i, которая является собственным значением оператора Фока молекулы: электроны заполняют МО в порядке повышения энергии молекулы. Полная ХФ энергия молекулы с замкнутыми оболочками

_. (12)

Последний член описывает электростатическую энергию отталкивания ядер.

, (13)

, (14)

, (15)

. (16)

- кинетическая энергия электрона на орбитали _i(x) плюс его притяжение к ядрам, _i - полная энергия этого электрона в поле ядер и остальных электронов. Двухэлектронный кулоновский интеграл описывает энергию межэлектронного отталкивания электронов, а двухэлектронный обменный интеграл-понижение энергии взаимодействия электронов с параллельными спинами на орбиталях_i(x) и _j(x).

3. Приближение мо лкао. Уравнения Рутана

Двигаясь по молекуле, каждый электрон попадает под преимущественное влияние поля ядра, вблизи которого он находится в данный момент. Поэтому каждую МО можно представить как линейную комбинацию всех АО:

. (17)

(приближение МО ЛКАО). С учетом ортонормировки МО _(r)_(r)dV=_, из условия минимума энергии получают уравнения ХФ в виде

(18)

Это уравнения Рутана.

Элементы матрицы Фока F_ в приближении МО ЛКАО:

, (19)

_{, (20)}

_{, (21) , (22)}

S_ij = _ (r)_(r)dV –матрица интегралов перекрывания между АО _ и _. Е_ - _{энергия состояния .} – есть одно из решений секулярного уравнения

(23)

Уравнения Рутана в матричном виде:

F C = S C E. (24)

Путем унитарных преобразований F⁺=S^-1/2FS^-1/2 и C⁺=S^-1/2C решение уравнения (23) сводится к стандартной задаче на собственные значения

F⁺C⁺= EC⁺. (25)

Матрица P c элементами

(26)

(суммирование по занятым МО) называется матрицей зарядов- порядков связей или матрицей плотности. Она играет важную роль в теории химической связи, описывая распределение электронной плотности по молекуле.

Электронная энергия молекулы с закрытыми оболочками в терминах введенных обозначений записывается в методе Рутана следующим образом:

. (27)

Решение уравнений Рутана осуществляется итерационным методом ССП. Блок-схема вычислительного процесса представлена на рис. 6.

Число двухэлектронных кулоновских и обменных интегралов по АО равно _{ N4}/8, где N - число АО, т.е. очень велико, особенно, если все четыре орбитали _, _, _ и _{ центрированы на разных ядрах} (число одно электронных интегралов h_{ равно  N2/2 – см. табл. 4).}

Таблица 4. Число одноэлектронных и двухэлектронных интегралов

в минимальном базисе атомных орбиталей [2]

молекула	Атомные орбитали		Одноэлектронные интегралы	двухэлектронные интегралы	общее число
	N	тип АО
Н2 CH4 бензол C6H6	2 9 36	1s 1s-, 2s-, 2p- АО углерода, 1s-AO водорода 1s-, 2s-, 2p-AO углерода, 1s-AO водорода	3 45 666	6 1035 222111	9 1080 222777

Рис. 6. Блок-схема вычислительного процесса решения уравнений Рутана

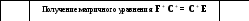
нет

да

Многоэлектронная волновая функция и энергии состояний, получаемые с помощью метода Хартри-Фока, инвариантны относительно ортогонального преобразования занятых электронами спин-орбиталей. Следствие: если вместо АО для построения МО (17) использовать их линейные комбинации, полученные с помощью ортогональных преобразований, то одновременно и согласовано изменятся все одно- и двухэлектронные интегралы и матрица P. Волновая функция (10) и энергия системы (27) при этом не изменятся.

Это очень важное свойство метода: используя его, всегда можно обеспечить концептуальную химическую трактовку результатов, например, перейти к локализованным МО, описывающим электроны связи и неподеленные электронные пары, гибридизованным АО и т.д.

Ортогональным преобразованием называется преобразование, которое не меняет длин векторов и углов между ними и переводит один ортонормированный базис в другой ортонормированный. Матрица ортогонального преобразования Т обладает свойствами: ТТ' = 1, det T =1.

Реально в расчеты включается конечное число АО. Чтобы воспроизвести точное ХФ решение, потребовалось бы использовать в разложении (16) бесконечное число функций - хартри-фоковский предел.