
Menshikov_RinochnRiskiModeliMetodi
.pdf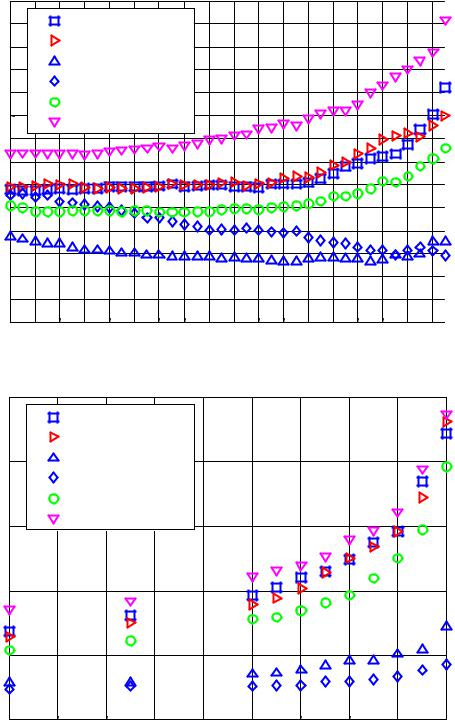
K 1.6 |
CW |
|
1.5 |
||
1.4 |
EW(λ =0.90) |
|
EW(λ =0.97) |
||
1.3 |
||
EVT |
||
1.2 |
||
GARCH(1,1) |
||
1.1 |
||
Wavelet |
||
1 |
|
|
0.9 |
|
|
0.8 |
|
|
0.7 |
|
|
0.6 |
|
|
0.5 |
|
|
0.4 |
|
|
0.3 |
|
|
0.2 |
|
|
80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 |
||
|
Уровень достоверности, % |
|
K |
5 |
|
CW |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EW(λ |
=0.90) |
|
|
|
|
|
|
|
4 |
|
EW(λ |
=0.97) |
|
|
|
|
|
|
|
|
|
EVT |
|
|
|
|
|
|
|
|
|
|
GARCH(1,1) |
|
|
|
|
|
|
|
|
3 |
|
Wavelet |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
98.2 |
98.4 |
98.6 |
98.8 |
99 |
99.2 |
99.4 |
99.6 |
99.8 |
|
98 |
|||||||||
|
|
|
Уровень достоверности, % |
|
|
|
||||
Рис. 12. Сравнение точности моделей VaR на рынке EQRU
41
K |
1.6 |
|
|
|
|
|
Wavelet |
||
|
|
|
|
|
|
1.4 |
|
|
GARCH(1,1) |
|
|
|
EVT |
|
|
|
|
|
|
|
1.2 |
|
|
EW(λ =0.97) |
|
|
|
EW(λ =0.90) |
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
CW |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.8
0.6 0.4
0.4
0.280 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97
Уровень достоверности, %
K 9 |
|
Wavelet |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
||
|
GARCH(1,1) |
|
|
|
|
|
|
||
7 |
|
EVT |
|
|
|
|
|
|
|
|
EW(λ =0.97) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
6 |
|
EW(λ =0.90) |
|
|
|
|
|
|
|
|
CW |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
98.2 |
98.4 |
98.6 |
98.8 |
99 |
99.2 |
99.4 |
99.6 |
99.8 |
98 |
|||||||||
Уровень достоверности, %
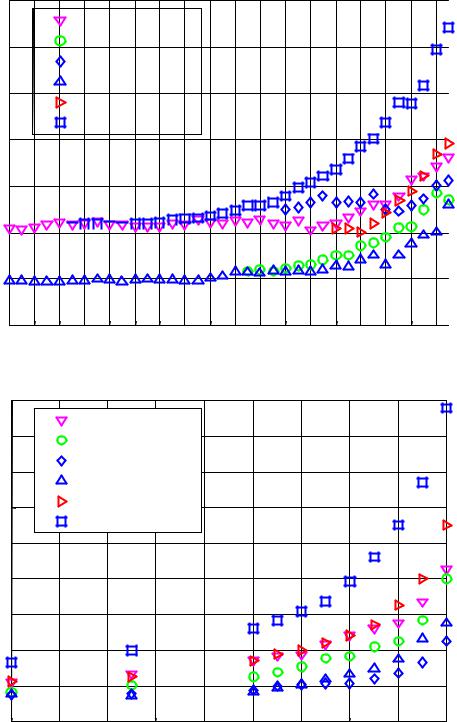
Рис. 13. Сравнение точности моделей VaR на рынке FS
42
3.3.1. Относительная функция потерь
Относительная функция, или средний непокрытый риск, учитывает величины превышений оценки риска:
|
|
|
∆ P |
+ 1 |
|
− |
VaR |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
t |
|
|
|
t |
, если |
|
∆ P |
+ 1 |
> |
VaR |
|
|||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Lt + 1 = |
|
|
|
VaR |
|
|
|
|
|
|
|
t |
|
t |
(49) |
|||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
0, |
t |
если |
|
∆ Pt + 1 |
|
≤ VaRt . |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
В отличие от бинарной функции потерь данная статистика анализирует только относительные величины превышений, не учитывая их частоту. Таким образом, среднее значение функции показывает, насколько в среднем в случае превышения уровня VaR мы ошибаемся. Чем меньше значение статистики у модели, тем она эффективнее в данном аспекте. Из результатов можно сделать следующие выводы.
1) На относительно «спокойном» рынке FX у всех моделей среднее значение приблизительно одинаково, что обусловлено хорошим согласием реальных данных и предположений модели. На рынке FS, как и должно было быть, наилучшие результаты у модели экстремальных значений. В целом по всем рынкам можно особо выделить модель Wavelet как наиболее стабильную.
2)При анализе результатов необходимо учитывать, что на среднее значение влияет и количество превышений. Так, для модели, имеющей большое количество малых превышений, значение этого теста может быть очень неплохим, в то время, как у другой модели, ее доминирующей, с меньшим числом превышений значение теста может быть больше. Этот недостаток можно частично устранить, умножив значение VaR на значение множителя, обеспечивающего покрытие для рассматриваемой модели, тем самым приведя все модели к «общему знаменателю».
3.3.2.Средний неиспользованный риск
Данный тест фактически является дополнительным к предыдущему тесту на средний непокрытый риск и показывает, насколько в среднем оценка VaR превышает реализовавшиеся прибыли/убытки, т.е. характеризует неиспользованный рисковый капитал. Функция потерь при этом имеет вид
|
VaR − |
|
∆ |
P |
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ft + 1 = |
|
t |
|
|
t |
|
|
, |
если |
|
∆ P |
+ 1 |
|
> VaR |
, |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
VaR |
|
|
|
|
|
|
|
t |
|
t |
|
(50) |
||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
t |
|
0 |
иначе. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Зарезервированный рисковый капитал не приносит дохода, поэтому желательно, чтобы значение неиспользованного рискового капитала было как
43
можно меньше. Этот критерий становится еще более важным для банков, так как они согласно BIS должны резервировать капитал, равный 3*VaR. Поэтому даже небольшое улучшение эффективности по данному критерию может принести значительную выгоду. Согласно результатам теста, приведенным в табл. 6-7, по этому критерию модель Wavelet доминирует над остальными на всех рынках.
3.3.3. Многокритериальный анализ моделей
Предыдущие два теста можно проанализировать вместе, разместив на двумерной плоскости соответствующие точки (рис. 14-16). По этим графикам можно определить парето-оптимальные модели, когда считается, что модель доминирует другую, если имеет меньший непокрытый и неиспользованный риск.
В целом по всем рынкам парето-оптимальными или близкими к таковым являются модели GARCH(1,1), EVT и Wavelet, причем характеристики модели Wavelet являются наиболее стабильными по всем рынкам. Таким образом, при выборе для практического использования модели из группы оптимальных по Парето для любых внешних рыночных условиях их использование будет экономически более эффективным, чем использование остальных доминируемых моделей.
|
0,39 |
|
|
|
|
|
риск |
0,38 |
|
|
|
|
|
|
|
|
|
|
|
|
непокрытый |
0,37 |
|
|
|
|
|
0,36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Средний |
0,35 |
|
|
|
|
|
0,34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,33 |
|
|
|
|
|
|
0,972 |
0,974 |
0,976 |
0,978 |
0,980 |
0,982 |
|
|
Средний неиспользованный риск |
|
|||
 CW
CW

 EW(0.90)
EW(0.90)
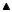 EW(0.97)
EW(0.97)
 EVT
EVT
 GARCH(1,1)
GARCH(1,1)
 Wavelet
Wavelet
Рис. 14. График среднее превышение/средний неиспользованный риск для рынка FX и уровня достоверности 95%
3.3.4. Корреляция VaR и реальных убытков
Этот простой тест, состоящий в измерении корреляции между значением VaR и абсолютным значением изменения стоимости портфеля, показывает степень зависимости между прогнозами VaR, осуществляемыми моделью, и
44
|
1,6 |
|
|
|
|
|
риск |
1,4 |
|
|
|
|
CW |
1,2 |
|
|
|
|
||
непокрытый |
|
|
|
|
||
|
|
|
|
EW(0.90) |
||
1,0 |
|
|
|
|
||
|
|
|
|
EW(0.97) |
||
|
|
|
|
|
||
0,8 |
|
|
|
|
EVT |
|
0,6 |
|
|
|
|
GARCH(1,1) |
|
Средний |
0,4 |
|
|
|
|
Wavelet |
|
|
|
|
|
||
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0 |
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
|
|
Средний неиспользованный риск |
|
|||
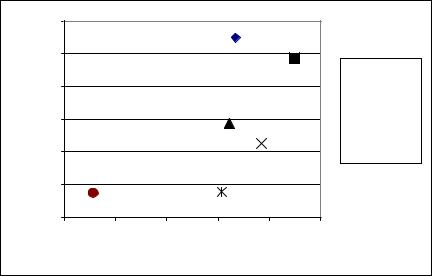
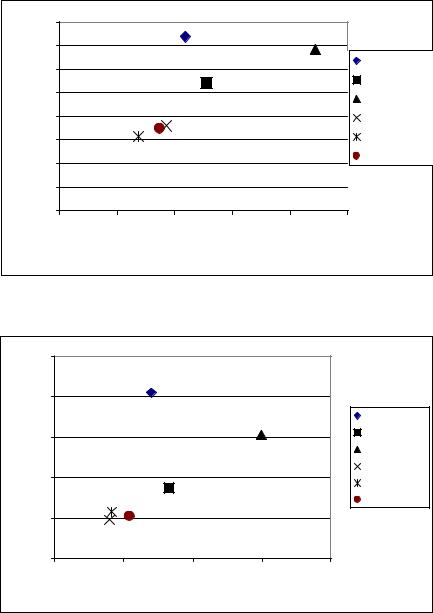
Рис. 15. График среднее превышение/средний неиспользованный риск для |
||||||
|
рынка EQRU и уровня достоверности 95% |
|||||
|
2,5 |
|
|
|
|
риск |
2,0 |
|
|
|
|
|
|
|
|
CW |
|
непокрытый |
|
|
|
|
|
1,5 |
|
|
|
EW(0.90) |
|
|
|
|
EW(0.97) |
||
|
|
|
|
||
1,0 |
|
|
|
EVT |
|
|
|
|
GARCH(1,1) |
||
Средний |
|
|
|
||
|
|
|
|
||
|
|
|
|
Wavelet |
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
0,0 |
|
|
|
|
|
0,0 |
2,0 |
4,0 |
6,0 |
8,0 |
|
|
Средний неиспользованный риск |
|
||
Рис. 16. График среднее превышение/средний неиспользованный риск для |
|||||
|
|
рынка FS и уровня достоверности 99% |
|||
реализовавшимися прибылью/убытками. Более эффективным моделям, как осуществляющим более точный прогноз, должны соответствовать большие коэффициенты корреляции.
Результаты теста приведены в табл. 10. Наибольший коэффициент корреляции имеет модели Wavelet и GARCH, из чего можно сделать вывод об их большей эффективности для прогноза изменений (уменьшения или увеличения) волатильности.
45
Заключение
Результаты данной работы свидетельствуют о том, что традиционные параметрические модели, используемые для вычисления меры риска VaR и широко применяемые на развитых рынках, могут оказаться непригодны для использования на развивающихся и нестабильных рынках без тонкой настройки и постоянной корректировки параметров модели. Такие выводы сделаны на основе исследования статистических свойств исторических временных рядов, а также прогонки моделей на тестовых выборках. Показано, что применение традиционных параметрических моделей не дает надежных оценок риска.
В то же время показано, что применение полупараметрических моделей: модели, использующей теорию экстремальных значений, а также предложенной в работе модели, использующей вейвлет-анализ для непараметрической оценки волатильности, - дает хорошие результаты даже на таких рынках. Более того, при многокритериальном анализе эффективности данные модели VaR также доминируют традиционные модели, в том числе и на стабильных рынках. Полученные результаты позволяют сделать вывод о применимости предложенной модели расчета VaR для портфелей, состоящих из инструментов, относящихся к разнородным рынкам: как к стабильным, так и к развивающимся.
46
Приложения
Приложение 1. Введение в вейвлет-анализ
Вейвлет-анализ аналогично Фурье-анализу заключается в декомпозиции исходного сигнала на элементарные составляющие, представляющие собой растяжения и сдвиги одной (или нескольких) базисной функции ψ (t),
называемой “материнской” (mother wavelet): |
|
||||||
|
1 |
|
t − |
a |
|
|
|
ψ a,b (t) = |
ψ |
|
|
, t |
R, a,b |
R, a > 0. |
|
a |
|
||||||
|
|
b |
|
|
|
|
|
Определение. Одномерным вейвлетом порядка m с компактным носителем называется функция ψ (t), такая что
1.ψ имеет ограниченные производные до m включительно, определенные почти всюду на интервале (a,b).
2.ψ равна нулю вне интервала (a,b).
3.ψ имеет нулевые моменты до m-го включительно:
|
b |
|
|
|
|
|
∫ |
|
|||
|
tα |
ψ (t)dt = 0,α = |
o,m |
. |
|
|
a |
|
|
|
|
4. Семейство |
{ψ jk (t) = |
2 j / 2ψ (2 j t − k)} , j, k Z |
является |
||
ортонормированным базисом в L2( R ).
Можно рассматривать вейвлеты, определенные на всей числовой оси, при этом
в определении a = |
−∞ |
и b = +∞ и дополнительно требуется ограниченность |
||||
|
∞ |
(t) |
|
2 dt < |
∞ . |
|
L2-нормы: |
|
ψ |
|
|||
|
||||||
|
∫ |
|
|
|
|
|
− ∞
Характерный вид одного из семейств вейвлет показан на рис. 17.
Теперь определим интегральное (непрерывное) вейвлет - преобразование сигнала f(t):
[Wψ f ](a,b) = ∫f (t)ψ a,b (t)dt ,
Свойства вейвлет-преобразования:
1.Линейность: W[α f1(t)+β f2(t)]=α W[f1]+β W[f2].
2.Инвариантность относительно сдвига: W[f(t-b0)]=W(a,b-b0).
3.Инвариантность относительно изменения масштаба:
|
t |
|
|
W |
|
|
= |
f |
|
||
|
a0 |
|
|
1 |
|
|
b |
|
|
a |
, |
|
|||
|
|
||||
a0 |
W |
a0 |
. |
||
a0 |
|
|
47

Рис. 17. Примеры вейвлет
Дискретное вейвлет-преобразование. Пусть дана последовательность (временной ряд) {xi}iN= 1 , N = 2J . Дискретное вейвлет-
преобразование определяется в терминах фильтров Н и G, а также «прореживающего» оператора D0, определяемых ниже.
Фильтр H задается последовательностью {hk}, а его действие на ряд {xn} |
|||||
|
(Hx)k = ∑ hn− k xn , |
|
|
|
|
|
|
n |
|
|
|
причем фильтр должен удовлетворять условию ортогональности |
|||||
∑ |
h h |
= 0, j ≠ 0 и h2 |
= |
1. |
|
n n+ 2 j |
∑ |
n |
|
|
|
n |
|
n |
|
|
|
Фильтр G – «зеркальный» фильтр (mirror filter) определяется
последовательностью g |
n |
= (− |
1)n h |
. |
||||
|
|
|
|
|
|
1− n |
|
|
|
|
Действие оператора D0 |
определяется как (D0 x) j = x2 j , т.е. выбирает |
|||||
только четные члены последовательности. |
||||||||
Определим cJ |
≡ x ,n = |
0,1,...,2J − 1. Для J=J-1,…,0 рекурсивно определим |
||||||
|
|
n |
|
n |
|
|
|
|
c j |
= |
D Hc j+ |
1 |
- сглаженные коэффициенты на j-м уровне, а |
||||
|
|
0 |
|
|
|
|
|
|
d j |
= |
D Gc j + |
1 |
- детализированные коэффициенты на j-м уровне. |
||||
|
|
0 |
|
|
|
|
|
|
Заметим, что c j и d j – последовательности длины 2j.
48
Так как и D0H, и D0G являются ортогональными преобразованиями, то обратное преобразование найти просто, если записать преобразование в матричной форме и в качестве обратного преобразования взять обратную матрицу.
позволяет более полно исследовать статистические свойства исходных данных, не уменьшая числа коэффициентов разложения на каждом последующем уровне, но в то же время является переопределенным, что влечет некоторые трудности.
Определим |
оператор Z, вставляющий в последовательность нули: |
|||
Z : (Zx)2 j = xj , (Zx)2 j + 1 = 0. |
|
|
||
Определим |
стационарное |
вейвлет-преобразование |
аналогично |
|
дискретному, только осуществляемое посредством операторов H[r ] и G[r] : |
||||
H[r ] = Z r h, |
G[r ] = Z r g , |
|
|
|
aJ=cJ, |
|
|
|
|
a j− 1 = H[ J − j]a j , b j − 1 = G[ J − j]a j .
Если вектор aJ имеет длину 2J, то преобразование требует O(J2J) операций в отличие от O(2J) операций в случае дискретного вейвлетпреобразования. Стационарное преобразование связано с непрерывным, так как его коэффициенты можно находить как
dkj = ∫ψ j (t − 2− J k) f (t)dt .
С помощью стационарного вейвлет-преобразования выражаются функции локальной автоковарации, и, следовательно, эволюционный вейвлет-спектр имеет вид
S(t) = ∑− 1 (dkj )2 .
j = −∞
Приложение 2. Алгоритм дискретного стационарного вейвлет-преобразования
Пусть X = (x1,..., xn ) |
- исходный сигнал, G = (g1,..., gm )- фильтр. Как |
||||
описано в приложении 1, |
для стационарного преобразования используется |
||||
фильтр G[r ] = |
|
|
|
|
|
g |
,0,...,0, g |
2 |
,...,0,...,0, g |
. |
|
|
1 |
$#" |
$#" |
m |
|
|
|
2r − 1 |
|
2r − 1 |
|
49

Вектор Y, полученный в результате свертки X и G[r] имеет компоненты
mr |
xi gk + i− 1 и длину n-mr+1, |
|
|
|
|
|||
yk = ∑ |
|
|
|
|
||||
i= 1 |
|
|
|
|
|
|
n − 1 |
|
где m = |
(m − 1)(2 |
r |
− 1) + m и r |
≤ |
J = log |
|
|
|
|
|
|
. |
|||||
r |
|
|
|
|
|
2 |
m − 1 |
|
Таким образом, для того чтобы получить необходимое число коэффициентов (k=1,…,n), необходимо добавить к X еще mr-1 значений. Причем добавить надо таким образом, чтобы сохранить l2 – норму. Для этого выберем
следующее граничное расширение:
~ =
X (xn− mr + 1,..., xn , x1,..., xn ).
В результате получаем следующий алгоритм.
0. |
Устанавливаем уровень j=0. |
|
~ |
, G |
[ j] |
, H |
[ j] |
|
|||||
1. |
На уровне j получаем векторы |
по приведенным выше |
|||||||||||
X |
|
|
|||||||||||
|
формулам. |
~ |
|
G |
[ |
j] |
и H |
[ j] |
|
|
|||
2. |
|
с |
- получаем значения |
||||||||||
Производим свертку X |
|
|
|
||||||||||
коэффициентов на уровне j.
3.Увеличиваем значения уровня j=j+1, и если j<J, то переходим к шагу 1.
Приложение 3. Результаты тестов
Модель |
FX |
EQRU |
|
FS |
|||
|
L |
σ |
L |
σ |
L |
|
σ |
CW |
0,0555 |
0,0035 |
0,0463 |
0,0057 |
0,0533 |
|
0,0076 |
EW90 |
0,0622 |
0,0037 |
0,0499 |
0,0067 |
0,0399 |
|
0,0129 |
EW97 |
0,0546 |
0,0077 |
0,0253 |
0,0134 |
0,0331 |
|
0,0137 |
EVT |
0,0531 |
0,0075 |
0,0492 |
0,0068 |
0,0466 |
|
0,0088 |
GARCH |
0,0508 |
0,0029 |
0,0439 |
0,0105 |
0,0283 |
|
0,0161 |
Wavelet |
0,0647 |
0,0059 |
0,0628 |
0,0048 |
0,0403 |
|
0,0075 |
Таблица 2. Среднее значение бинарной функции потерь при уровне достоверности 95%
50
