e-maxx_algo

клетка) изначально находится робот. Робот может двигаться только вправо или вверх, и в итоге он должен попасть

в клетку , избежав все препятствия. Требуется посчитать число путей, которыми он может это сделать. Предполагаем, что размеры и очень большие (скажем, до ), а количество — небольшое (порядка ).

Для решения сразу в целях удобства отсортируем препятствия в том порядке, в каком мы можем их обойти: т. е., например, по координате , а при равенстве — по координате .

Также сразу научимся решать задачу без препятствий: т.е. научимся считать число способов дойти от одной клетки до другой. Если по одной координате нам надо пройти клеток, а по другой — клеток, то из несложной комбинаторики мы получаем такую формулу через биномиальные коэффициенты:

Теперь чтобы посчитать число способов дойти от одной клетки до другой, избежав всех препятствий, можно воспользоваться формулой включений-исключений: посчитаем число способов дойти, наступив хотя бы на одно препятствие.

Для этого можно, например, перебрать подмножество тех препятствий, на которые мы точно наступим, посчитать число способов сделать это (просто перемножив число способов дойти от стартовой клетки до первого из выбранных препятствий, от первого препятствия до второго, и так далее), и затем прибавить или отнять это число от ответа, в соответствии со стандартной формулой включений-исключений.

естественно). Всего у нас будет точки, поскольку к препятствиям добавляются стартовая и конечная клетки.

Если мы на секунду забудем про все препятствия и просто посчитаем число путей из клетки в клетку , то тем самым мы учтём некоторые "плохие" пути, проходящие через препятствия. Научимся считать количество этих "плохих"

Число взаимно простых четвёрок

Дано чисел: . Требуется посчитать количество способов выбрать из них четыре числа так, что их совокупный наибольший общий делитель равен единице.

Будем решать обратную задачу — посчитаем число "плохих" четвёрок, т.е. таких четвёрок, в которых все числа делятся на число .

Воспользуемся формулой включений-исключений, суммируя количество четвёрок, делящихся на делитель (но, возможно, делящихся и на больший делитель):

где — это количество простых в факторизации числа , — количество четвёрок, делящихся на .

Чтобы посчитать функцию , надо просто посчитать количество чисел, кратных , и биномиальным коэффициентом посчитать число способов выбрать из них четвёрку.

Таким образом, с помощью формулы включений-исключений мы суммируем количество четвёрок, делящихся на простые числа, затем отнимаем число четвёрок, делящихся на произведение двух простых, прибавляем четвёрки, делящиеся на три простых, и т.д.

Число гармонических троек

Во-первых, сразу перейдём к обратной задаче — т.е. посчитаем число негармонических троек.

Во-вторых, заметим, что в любой негармонической тройке ровно два её числа находятся в такой ситуации, что это число взаимно просто с одним числом тройки и не взаимно просто с другим числом тройки.

и приблизительно равно числу:

(более того, если округлить это выражение к ближайшему целому — то получится в точности число перестановок без неподвижных точек)

Обозначим через множество перестановок длины с неподвижной точкой в позиции (). Воспользуемся теперь формулой включений-исключений, чтобы посчитать число перестановок хотя бы с

поскольку если мы знаем, что число неподвижных точек равно , то тем самым мы знаем позицию элементов перестановки, а все остальные элементов могут стоять где угодно.

Подставляя это в формулу включений-исключений и учитывая, что число способов выбрать подмножество размера из -элементного множества равно , получаем формулу для числа перестановок хотя бы с одной неподвижной точкой:

Тогда число перестановок без неподвижных точек равно:

Упрощая это выражение, получаем точное и приблизительное выражения для количества перестановок без неподвижных точек:

(поскольку сумма в скобках — это первые членов разложения в ряд Тейлора )

В заключение стоит отметить, что аналогичным образом решается задача, когда требуется, чтобы неподвижных точек не было среди первых элементов перестановок (а не среди всех, как мы только что решали). Формула получится такая, как приведённая выше точная формула, только в ней сумма будет идти до , а не до .

Задачи в online judges

Список задач, которые можно решить, используя принцип включений-исключений:

Литература

● Debra K. Borkovitz. "Derangements and the Inclusion-Exclusion Principle"

Игры на произвольных графах

Пусть игра ведётся двумя игроками на некотором графе G. Т.е. текущее состояние игры - это некоторая вершина графа, и из каждой вершины рёбра идут в те вершины, в которые можно пойти следующим ходом.

Мы рассматриваем самый общий случай - случай произвольного ориентированного графа с циклами. Требуется для заданной начальной позиции определить, кто выиграет при оптимальной игре обоих игроков (или определить, что результатом будет ничья).

Мы решим эту задачу очень эффективно - найдём ответы для всех вершин графа за линейное относительно количества рёбер время - O (M).

Описание алгоритма

Про некоторые вершины графа заранее известно, что они являются выигрышными или проигрышными; очевидно, такие вершины не имеют исходящих рёбер.

Имеем следующие факты:

●если из некоторой вершины есть ребро в проигрышную вершину, то эта вершина выигрышная;

●если из некоторой вершины все рёбра исходят в выигрышные вершины, то эта вершина проигрышная;

●если в какой-то момент ещё остались неопределённые вершины, но ни одна из них не подходят ни под первое, ни под второе правило, то все эти вершины - ничейные.

Таким образом, уже ясен алгоритм, работающий за асимптотику O (N M) - мы перебираем все вершины, пытаемся

к каждой применить первое либо второе правило, и если мы произвели какие-то изменения, то повторяем всё заново. Однако этот процесс поиска и обновления можно значительно ускорить, доведя асимптотику до линейной.

Переберём все вершины, про которые изначально известно, что они выигрышные или проигрышные. Из каждой из них пустим следующий поиск в глубину. Этот поиск в глубину будет двигаться по обратным рёбрам. Прежде всего, он не будет заходить в вершины, которые уже определены как выигрышные или проигрышные. Далее, если поиск в глубину пытается пойти из проигрышной вершины в некоторую вершину, то её он помечает как выигрышную, и идёт в неё. Если же поиск в глубину пытается пойти из выигрышной вершины в некоторую вершину, то он должен проверить, все ли рёбра ведут из этой вершины в выигрышные. Эту проверку легко осуществить за O (1), если в каждой вершине будем хранить счётчик рёбер, которые ведут в выигрышные вершины. Итак, если поиск в глубину пытается пойти из выигрышной вершины в некоторую вершину, то он увеличивает в ней счётчик, и если счётчик сравнялся

с количеством рёбер, исходящих из этой вершины, то эта вершина помечается как проигрышная, и поиск в глубину идёт

вэту вершину. Иначе же, если целевая вершина так и не определена как выигрышная или проигрышная, то поиск

вглубину в неё не заходит.

Итого, мы получаем, что каждая выигрышная и каждая проигрышная вершина посещается нашим алгоритмом ровно один раз, а ничейные вершины и вовсе не посещаются. Следовательно, асимптотика действительно O (M).

Реализация

Рассмотрим реализацию поиска в глубину, в предположении, что граф игры построен в памяти, степени исхода посчитаны и записаны в degree (это будет как раз счётчиком, он будет уменьшаться, если есть ребро в выигрышную вершину), а также изначально выигрышные или проигрышные вершины уже помечены.

vector<int> g [100]; bool win [100];

bool loose [100]; bool used[100]; int degree[100];

void dfs (int v) { used[v] = true;

for (vector<int>::iterator i = g[v].begin(); i != g[v].end(); ++i) if (!used[*i]) {

if (loose[v])

win[*i] = true; else if (--degree[*i] == 0)

loose[*i] = true;

else

continue; dfs (*i);

}

}

Пример задачи. "Полицейский и вор"

Чтобы алгоритм стал более ясным, рассмотрим его на конкретном примере.

Условие задачи. Имеется поле размером MxN клеток, в некоторые клетки заходить нельзя. Известны начальные координаты полицейского и вора. Также на карте может присутствовать выход. Если полицейский окажется в одной клетке с вором, то выиграл полицейский. Если же вор окажется в клетке с выходом (и в этой клетке не стоит полицейский), то выиграет вор. Полицейский может ходить в 8 направлениях, вор - только в 4 (вдоль осей координат). И полицейский, и вор могут пропустить свой ход. Первым ход делает полицейский.

Построение графа. Построим граф игры. Мы должны формализовать правила игры. Текущее состояние игры определяется координатами полицейского P, вора T, а также булева переменная Pstep, которая определяет, кто будет делать следующий ход. Следовательно, вершина графа определена тройкой (P,T,Pstep). Граф построить легко, просто соответствуя условию.

Далее нужно определить, какие вершины являются выигрышными или проигрышными изначально. Здесь есть тонкий момент. Выигрышность/проигрышность вершины помимо координат зависит и от Pstep - чей сейчас ход. Если сейчас ход полицейского, то вершина выигрышная, если координаты полицейского и вора совпадают; вершина проигрышная, если она не выигрышная и вор находится на выходе. Если же сейчас ход вора, то вершина выигрышная, если вор находится на выходе, и проигрышная, если она не выигрышная и координаты полицейского и вора совпадают.

Единственный момент, которой нужно решить - строить граф явно или делать это "на ходу", прямо в поиске в глубину. С одной стороны, если строить граф предварительно, то будет меньше вероятность ошибиться. С другой стороны, это увеличит объём кода, да и время работы будет в несколько раз медленнее, чем если строить граф "на ходу".

Реализация всей программы:

struct state { char p, t; bool pstep;

};

vector<state> g [100][100][2];

// 1 = policeman coords; 2 = thief coords; 3 = 1 if policeman's step or 0 if thief's.

bool win [100][100][2]; bool loose [100][100][2]; bool used[100][100][2]; int degree[100][100][2];

void dfs (char p, char t, bool pstep) { used[p][t][pstep] = true;

for (vector<state>::iterator i = g[p][t][pstep].begin(); i != g[p] [t][pstep].end(); ++i)

if (!used[i->p][i->t][i->pstep]) { if (loose[p][t][pstep])

win[i->p][i->t][i->pstep] = true; else if (--degree[i->p][i->t][i->pstep] == 0)

loose[i->p][i->t][i->pstep] = true;

else

continue;

dfs (i->p, i->t, i->pstep);

}

}

int main() {

int n, m;

cin >> n >> m; vector<string> a (n); for (int i=0; i<n; ++i)

cin >> a[i];

for (int p=0; p<n*m; ++p)

for (int t=0; t<n*m; ++t)

for (char pstep=0; pstep<=1; ++pstep) {

int px = p/m, py = p%m, tx=t/m, ty=t%m;

if (a[px][py]=='*' || a[tx][ty]=='*') continue;

cout << (win[p_st][t_st][true] ? "WIN" : loose[p_st][t_st] [true] ? "LOSS" : "DRAW");

}

Теория Шпрага-Гранди. Ним

Введение

Теория Шпрага-Гранди — это теория, описывающая так называемые равноправные (англ. "impartial") игры двух игроков, т.е. игры, в которых разрешённые ходы и выигрышность/проигрышность зависят только от состояния игры. От того, какой именно из двух игроков ходит, не зависит ничего: т.е. игроки полностью равноправны.

Кроме того, предполагается, что игроки располагают всей информацией (о правилах игры, возможных ходах, положении соперника).

Предполагается, что игра конечна, т.е. при любой стратегии игроки рано или поздно придут в проигрышную позицию, из которой нет переходов в другие позиции. Эта позиция является проигрышной для

игрока, который должен делать ход из этой позиции. Соответственно, она является выигрышной для игрока, пришедшего в эту позицию. Понятно, ничейных исходов в такой игре не бывает.

Иными словами, такую игру можно полностью описать ориентированным ациклическим графом: вершинами в нём являются состояния игры, а рёбрами — переходы из одного состояния игры в другое в результате хода текущего игрока (повторимся, в этом первой и второй игрок равноправны). Одна или несколько

вершин не имеют исходящих рёбер, они является проигрышными вершинами (для игрока, который должен совершать ход из такой вершины).

Поскольку ничейных исходов не бывает, то все состояния игры распадаются на два класса: выигрышные и проигрышные. Выигрышные — это такие состояния, что найдётся ход текущего игрока, который приведёт

к неминуемому поражению другого игрока даже при его оптимальной игре. Соответственно, проигрышные состояния — это состояния, из которых все переходы ведут в состояния, приводящие к победе второго игрока, несмотря на "сопротивление" первого игрока. Иными словами, выигрышным будет состояние, из которого есть хотя бы один переход в проигрышное состояние, а проигрышным является состояние, из которого все переходы ведут в выигрышные состояния (или из которого вообще нет переходов).

Наша задача — для любой заданной игры провести классификацию состояний этой игры, т.е. для каждого состояния определить, выигрышное оно или проигрышное.

Теорию таких игр независимо разработали Роланд Шпраг (Roland Sprague) в 1935 г. и Патрик Майкл Гранди (Patrick Michael Grundy) в 1939 г.

Игра "Ним"

Эта игра является одним из примеров описываемых выше игр. Более того, как мы увидим чуть позже, любая из равноправных игр двух игроков на самом деле эквивалентна игре "ним" (англ. "nim"), поэтому изучение этой игры автоматически позволит нам решать все остальные игры (впрочем, об этом позже).

Исторически, эта игра была популярна ещё в древние времена. Вероятно, игра берёт своё происхождение в Китае — по крайней мере, китайская игра "Jianshizi" очень похожа на ним. В Европе первые упоминания о ниме относятся к XVI в. Само название "ним" придумал математик Чарлз Бутон (Charles Bouton), который в 1901 г. опубликовал полный анализ этой игры. Происхождение названия "ним" доподлинно неизвестно.

Описание игры

Игра "ним" представляет из себя следующую игру.

Есть несколько кучек, в каждой из которых по нескольку камней. За один ход игрок может взять из какой-нибудь одной кучки любое ненулевое число камней и выбросить их. Соответственно, проигрыш наступает, когда ходов больше не осталось, т.е. все кучки пусты.

Итак, состояние игры "ним" однозначно описывается неупорядоченным набором натуральных чисел. За один ход разрешается строго уменьшить любое из чисел (если в результате число станет нулём, то оно удаляется из набора).

Решение нима

Решение этой игры опубликовал в 1901 г. Чарлз Бутон (Charles L. Bouton), и выглядит оно следующим образом.

Теорема. Текущий игрок имеет выигрышную стратегию тогда и только тогда, когда XOR-сумма размеров кучек отлична от нуля. В противном случае текущий игрок находится в проигрышном состоянии. (XOR-суммой чисел

называется выражение , где — операция побитового исключающего или)

Доказательство.

Основная суть приведённого ниже доказательства — в наличии симметричной стратегии

для противника. Мы покажем, что, оказавшись в состоянии с нулевой XOR-суммой, игрок не сможет выйти из этого состояния — при любом его переходе в состояние с ненулевой XOR-суммой у противника найдётся ответный ход, возвращающий XOR-сумму обратно в ноль.

Приступим теперь к формальному доказательству (оно будет конструктивным, т.е. мы покажем, как именно выглядит симметричная стратегия противника — какой именно ход нужно будет ему совершать).

Доказывать теорему будем по индукции.

Для пустого нима (когда размеры всех кучек равны нулю) XOR-сумма равна нулю, и теорема верна.

Пусть теперь мы хотим доказать теорему для некоторого состояния игры, из которого есть хотя бы один переход. Пользуясь предположением индукции (и ацикличностью игры) мы считаем, что теорема доказана для всех состояний, в которые мы можем попасть из текущего.

Тогда доказательство распадается на две части: если XOR-сумма в текущем состоянии , то надо доказать, что текущее состояние проигрышно, т.е. все переходы из него ведут в состояния с XOR-суммой . Если же

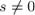, то надо доказать, что найдётся переход, приводящий нас в состояние с .

●Пусть , тогда мы хотим доказать, что текущее состояние — проигрышно. Рассмотрим любой переход из текущего состояния нима: обозначим через номер изменяемой кучки, через () — размеры кучек до хода, через () — после хода. Тогда, пользуясь элементарными свойствами функции , мы имеем:

е., согласно базе индукции, будет выигрышным, что и требовалось доказать.

● Пусть . Тогда наша задача — доказать, что текущее состояние — выигрышно, т.е. из него существует ход в проигрышное состояние (с нулевой XOR-суммой).

Рассмотрим битовую запись числа . Возьмём старший ненулевой бит, пусть его номер равен . Пусть — номер той кучки, у размер которой -ый бит отличен от нуля (такое найдётся, иначе бы в XOR-сумме этот бит

не получился бы отличным от нуля).

Тогда, утверждается, искомый ход — это изменить -ую кучку, сделав её размера . Убедимся в этом.

Теперь посчитаем, какая XOR-сумма получится при этом ходе:

Таким образом, указанный нами ход — действительно ход в проигрышное состояние, а это и доказывает, что текущее состояние выигрышно.

Теорема доказана.

Следствие. Любое состояние ним-игры можно заменить эквивалентным состоянием, состоящим из единственной кучки размера, равного XOR-сумме размеров кучек в старом состоянии.

Иными словами, при анализе нима с несколькими кучками можно посчитать XOR-сумму их размеров, и перейти к анализу нима из единственной кучки размера — как показывает только что доказанная теорема, выигрышность/проигрышность от этого не изменится.

Эквивалентность любой игры ниму. Теорема Шпрага-Гранди

Здесь мы покажем, как любой игре (равноправной игре двух игроков) поставить в соответствие ним. Иными словами, любому состоянию любой игры мы научимся ставить в соответствие ним-кучку, полностью описывающее состояние исходной игры.

Лемма о ниме с увеличениями

Докажем сначала очень важную лемму — лемму о ниме с увеличениями.

А именно, рассмотрим следующий модифицированный ним: всё так же, как и в обычном ниме, однако теперь разрешается дополнительный вид хода: вместо уменьшения, наоборот, увеличить размер некоторой кучки. Если быть более точным, то ход игрока теперь заключается в том, что он либо забирает ненулевое количество камней из какой-нибудь кучки, либо увеличивает размер какой-либо кучки (в