e-maxx_algo

Приведём здесь реализацию алгоритма Гаусса-Жордана с эвристикой partial pivoting (выбором опорного элемента как максимума по столбцу).

На вход функции передаётся сама матрица системы . Последний столбец матрицы — это в наших

старых обозначениях столбец свободных коэффициентов (так сделано для удобства программирования — т.к. в самом алгоритме все операции со свободными коэффициентами повторяют операции с матрицей ).

Функция возвращает число решений системы (, или ) (бесконечность обозначена в коде специальной константой , которой можно задать любое большое значение). Если хотя бы одно решение существует, то оно возвращается в векторе .

int gauss (vector < vector<double> > a, vector<double> & ans) { int n = (int) a.size();

int m = (int) a[0].size() - 1;

vector<int> where (m, -1);

for (int col=0, row=0; col<m && row<n; ++col) { int sel = row;

for (int i=row; i<n; ++i)

if (abs (a[i][col]) > abs (a[sel][col])) sel = i;

if (abs (a[sel][col]) < EPS) continue;

for (int i=col; i<=m; ++i)

swap (a[sel][i], a[row][i]); where[col] = row;

for (int i=0; i<n; ++i) if (i != row) {

double c = a[i][col] / a[row][col]; for (int j=col; j<=m; ++j)

a[i][j] -= a[row][j] * c;

}

++row;

}

ans.assign (m, 0);

for (int i=0; i<m; ++i)

if (where[i] != -1)

ans[i] = a[where[i]][m] / a[where[i]][i]; for (int i=0; i<n; ++i) {

double sum = 0;

for (int j=0; j<m; ++j)

sum += ans[j] * a[i][j]; if (abs (sum - a[i][m]) > EPS)

return 0;

}

for (int i=0; i<m; ++i)

if (where[i] == -1) return INF;

return 1;

}

В функции поддерживаются два указателя — на текущий столбец и текущую строку .

Также заводится вектор , в котором для каждой переменной записано, в какой строке должна она получиться (иными словами, для каждого столбца записан номер строки, в которой этот столбец отличен от нуля). Этот вектор нужен, поскольку некоторые переменные могли не "определиться" в ходе решения (т.е. это

независимые переменные, которым можно присвоить произвольное значение — например, в приведённой реализации это нули).

Реализация использует технику partial pivoting, производя поиск строки с максимальным по модулю элементом,

и переставляя затем эту строку в позицию (хотя явную перестановку строк можно заменить обменом двух индексов в некотором массиве, на практике это не даст реального выигрыша, т.к. на обмены тратится операций).

В реализации в целях простоты текущая строка не делится на опорный элемент — так что в итоге по окончании работы алгоритма матрица становится не единичной, а диагональной (впрочем, по-видимому, деление строки на ведущий элемент позволяет несколько уменьшить возникающие погрешности).

После нахождения решения оно подставляется обратно в матрицу — чтобы проверить, имеет ли система хотя бы одно решение или нет. Если проверка найденного решения прошла успешно, то функция возвращает или —

в зависимости от того, есть ли хотя бы одна независимая переменная или нет.

Асимптотика

Оценим асимптотику полученного алгоритма. Алгоритм состоит из фаз, на каждой из которых происходит:

●если опорный элемент в текущем столбце был найден — то прибавление текущего уравнения ко всем остальным уравнениям — за время

Очевидно, первый пункт имеет меньшую асимптотику, чем второй. Заметим также, что второй пункт выполняется не более раз — столько, сколько может быть зависимых переменных в СЛАУ.

Таким образом, итоговая асимптотика алгоритма принимает вид . При эта оценка превращается в .

Заметим, что когда СЛАУ рассматривается не в поле действительных чисел, а в поле по модулю два, то систему можно решать гораздо быстрее — об этом см. ниже в разделе "Решение СЛАУ по модулю".

Более точная оценка числа действий

Для простоты выкладок будем считать, что .

Как мы уже знаем, время работы всего алгоритма фактически определяется временем, затрачиваемым на исключение текущего уравнения из остальных.

Это может происходить на каждом из шагов, при этом текущее уравнение прибавляется ко всем остальным. При прибавлении работа идёт только со столбцами, начиная с текущего. Таким образом, в сумме получается

операций.

Дополнения

Ускорение алгоритма: разделение его на прямой и обратный ход

Добиться двукратного ускорения алгоритма можно, рассмотрев другую его версию, более классическую, когда алгоритм разбивается на фазы прямого и обратного хода.

В целом, в отличие от описанного выше алгоритма, можно приводить матрицу не к диагональному виду, а к треугольному виду — когда все элементы строго ниже главной диагонали равны нулю.

Система с треугольной матрицей решается тривиально — сначала из последнего уравнения сразу находится значение последней переменной, затем найденное значение подставляется в предпоследнее уравнение и находится значение предпоследней переменной, и так далее. Этот процесс и называется обратным ходом алгоритма Гаусса.

Прямой ход алгоритма Гаусса — это алгоритм, аналогичный описанному выше алгоритму Гаусса-Жордана, за одним исключением: текущая переменная исключается не из всех уравнений, а только из уравнений после текущего. В результате этого действительно получается не диагональная, а треугольная матрица.

Разница в том, что прямой ход работает быстрее алгоритма Гаусса-Жордана — поскольку в среднем он делает в

меньше алгоритма Гаусса-Жордана.

Решение СЛАУ по модулю

Для решения СЛАУ по модулю можно применять описанный выше алгоритм, он сохраняет свою корректность.

Разумеется, теперь становится ненужным использовать какие-то хитрые техники выбора опорного элемента — достаточно найти любой ненулевой элемент в текущем столбце.

Если модуль простой, то никаких сложностей вообще не возникает — происходящие по ходу работы алгоритма Гаусса деления не создают особых проблем.

Особенно замечателен модуль, равный двум: для него все операции с матрицей можно производить очень эффективно. Например, отнимание одной строки от другой по модулю два — это на самом деле их

симметрическая разность ("xor"). Таким образом, весь алгоритм можно значительно ускорить, сжав всю матрицу в

битовые маски и оперируя только ими. Приведём здесь новую реализацию основной части алгоритма ГауссаЖордана, используя стандартный контейнер C++ "bitset":

int gauss (vector < bitset<N> > a, int n, int m, bitset<N> & ans) { vector<int> where (m, -1);

for (int col=0, row=0; col<m && row<n; ++col) { for (int i=row; i<n; ++i)

if (a[i][col]) {

swap (a[i], a[row]); break;

}

if (! a[row][col]) continue; where[col] = row;

for (int i=0; i<n; ++i)

if (i != row && a[i][col]) a[i] ^= a[row];

++row;

}

Как можно заметить, реализация стала даже немного короче, при том, что она значительно быстрее старой реализации

— а именно, быстрее в 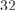раза за счёт битового сжатия. Также следует отметить, что решение систем по модулю два на практике работает очень быстро, поскольку случаи, когда от одной строки надо отнимать другую, происходят достаточно редко (на разреженных матрицах этот алгоритм может работать за время скорее порядка квадрата от размера, чем куба).

Если модуль произвольный (не обязательно простой), то всё становится несколько сложнее. Понятно, что пользуясь Китайской теоремой об остатках, мы сводим задачу с произвольным модулем только к модулям

вида "степень простого". [ дальнейший текст был скрыт, т.к. это непроверенная информация — возможно, неправильный способ решения ]

Наконец, рассмотрим вопрос числа решений СЛАУ по модулю. Ответ на него достаточно прост: число решений равно , где — модуль, — число независимых переменных.

Немного о различных способах выбора опорного элемента

Как уже говорилось выше, однозначного ответа на этот вопрос нет.

Эвристика "partial pivoting", которая заключалась в поиске максимального элемента в текущем столбце, работает на практике весьма неплохо. Также оказывается, что она даёт практически тот же результат, что и "full pivoting" —

когда опорный элемент ищется среди элементов целой подматрицы — начиная с текущей строки и с текущего столбца.

Но интересно отметить, что обе эти эвристики с поиском максимального элемента, фактически, очень зависят от того, насколько были промасштабированы исходные уравнения. Например, если одно из уравнений системы умножить на миллион, то это уравнение почти наверняка будет выбрано в качестве ведущего на первом же шаге. Это кажется достаточно странным, поэтому логичен переход к немного более сложной эвристике — так

называемому "implicit pivoting".

Эвристика implicit pivoting заключается в том, что элементы различных строк сравниваются так, как если бы обе строки были пронормированы таким образом, что максимальный по модулю элемент в них был бы равен единице. Для реализации этой техники надо просто поддерживать текущий максимум в каждой строке (либо поддерживать каждую строку так, чтобы максимум в ней был равен единице по модулю, но это может привести к увеличению накапливаемой погрешности).

Улучшение найденного ответа

Поскольку, несмотря на различные эвристики, алгоритм Гаусса-Жордана всё равно может приводить к большим погрешностям на специальных матрицах даже размеров порядка - .

В связи с этим, полученный алгоритмом Гаусса-Жордана ответ можно улучшить, применив к нему какой-либо простой численный метод — например, метод простой итерации.

Таким образом, решение превращается в двухшаговое: сначала выполняется алгоритм Гаусса-Жордана, затем — какой-либо численный метод, принимающий в качестве начальных данных решение, полученное на первом шаге.

Такой приём позволяет несколько расширить множество задач, решаемых алгоритмом Гаусса-Жордана с приемлемой погрешностью.

Литература

●William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes: The Art of Scientific Computing [2007]

●Anthony Ralston, Philip Rabinowitz. A first course in numerical analysis [2001]

Нахождение ранга матрицы

Ранг матрицы - это наибольшее число линейно независимых строк/столбцов матрицы. Ранг определён не только для квадратных матриц; пусть матрица прямоугольна и имеет размер NxM.

Также ранг матрицы можно определить как наибольший из порядков миноров матрицы, отличных от нуля.

Заметим, что если матрица квадратная и её определитель отличен от нуля, то ранг равен N(=M), иначе он будет меньше. В общем случае, ранг матрицы не превосходит min(N,M).

Алгоритм

Искать ранг можно с помощью модифицированного метода Гаусса. Будем выполнять абсолютно те же самые

операции, что и при решении системы или нахождении её определителя, но если на каком-либо шаге в i-ом столбце среди невыбранных до этого строк нет ненулевых, то мы этот шаг пропускаем, а ранг уменьшаем на единицу (изначально ранг полагаем равным max(N,M)). Иначе, если мы нашли на i-ом шаге строку с ненулевым элементом в i-

ом столбце, то помечаем эту строку как выбранную, и выполняем обычные операции отнимания этой строки от остальных.

Реализация

const double EPS = 1E-9;

int rank = max(n,m); vector<char> line_used (n); for (int i=0; i<m; ++i) {

int j;

for (j=0; j<n; ++j)

if (!line_used[j] && abs(a[j][i]) > EPS) break;

if (j == n) --rank;

else {

line_used[j] = true;

for (int p=i+1; p<m; ++p) a[j][p] /= a[j][i];

for (int k=0; k<n; ++k)

if (k != j && abs (a[k][i]) > EPS) for (int p=i+1; p<m; ++p)

a[k][p] -= a[j][p] * a[k][i];

}

}

Вычисление определителя матрицы методом Гаусса

Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.

Алгоритм

Воспользуемся идеями метода Гаусса решения систем линейных уравнений.

Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки,

что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).

Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный).

Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O (N3).

Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.

Реализация

const double EPS = 1E-9; int n;

vector < vector<double> > a (n, vector<double> (n));

... чтение n и a ...

double det = 1;

for (int i=0; i<n; ++i) { int k = i;

for (int j=i+1; j<n; ++j)

if (abs (a[j][i]) > abs (a[k][i])) k = j;

if (abs (a[k][i]) < EPS) { det = 0;

break;

}

swap (a[i], a[k]); if (i != k)

det = -det; det *= a[i][i];

for (int j=i+1; j<n; ++j) a[i][j] /= a[i][i];

for (int j=0; j<n; ++j)

if (j != i && abs (a[j][i]) > EPS) for (int k=i+1; k<n; ++k)

a[j][k] -= a[i][k] * a[j][i];

}

cout << det;

Вычисление определителя методом Краута за

O (N3)

Здесь будет рассмотрена модификация метода Краута (Crout), позволяющая вычислить определитель матрицы за O (N3).

Собственно алгоритм Краута находит разложение матрицы A в виде A = L U, где L - нижняя, а U - верхняя треугольная матрицы. Без ограничения общности можно считать, что в L все диагональные элементы равны 1. Но, зная эти матрицы, легко вычислить определитель A: он будет равен произведению всех элементов, стоящих на главной диагонали матрицы U.

Имеется теорема, согласно которой любая обратимая матрица обладает LU-разложением, и притом единственным, тогда и только тогда, когда все её главные миноры отличны от нуля. Следует напомнить, что мы рассматриваем только такие разложения, в которых диагональ L состоит только из единиц; иначе же, вообще говоря, разложение не единственно.

Пусть A - матрица, N - её размер. Мы найдём элементы матриц L и U. Сам алгоритм состоит из следующих шагов:

1.Положим Li i = 1 для i = 1, 2, ..., N

2.Для каждого j = 1, 2, ..., N выполним:

1.Для i = 1, 2, ..., j найдём значение Ui j: Ui j = Ai j - SUM Li k Uk j ,

где сумма по всем k = 1, 2, ..., i-1.

2.Далее, для i = j+1, j+2, ..., N имеем: Li j = (Ai j - SUM Li k Uk j) / Uj j ,

где сумма берётся по всем k = 1, 2, ..., j-1.

Реализация

Код на Java (с использованием дробной длинной арифметики):

static BigInteger det (BigDecimal a [][], int n)

{

try {

for (int i=0; i<n; i++)

{

boolean nonzero = false; for (int j=0; j<n; j++)

if (a[i][j].compareTo (new BigDecimal

(BigInteger.ZERO)) > 0)

nonzero = true;

if (!nonzero)

return BigInteger.ZERO;

}

BigDecimal scaling [] = new BigDecimal [n]; for (int i=0; i<n; i++)

{

BigDecimal big = new BigDecimal (BigInteger.ZERO); for (int j=0; j<n; j++)

if (a[i][j].abs().compareTo (big) > 0) big = a[i][j].abs();

scaling[i] = (new BigDecimal (BigInteger.ONE)) .divide (big, 100, BigDecimal.ROUND_HALF_EVEN);

}

int sign = 1;

for (int j=0; j<n; j++)

{

for (int i=0; i<j; i++)

{

BigDecimal sum = a[i][j]; for (int k=0; k<i; k++)

sum = sum.subtract (a[i][k].multiply (a[k][j])); a[i][j] = sum;

}

BigDecimal big = new BigDecimal (BigInteger.ZERO); int imax = -1;

for (int i=j; i<n; i++)

{

BigDecimal sum = a[i][j]; for (int k=0; k<j; k++)

sum = sum.subtract (a[i][k].multiply (a[k][j])); a[i][j] = sum;

BigDecimal cur = sum.abs();

cur = cur.multiply (scaling[i]); if (cur.compareTo (big) >= 0)

{

big = cur; imax = i;

}

}

if (j != imax)

{

for (int k=0; k<n; k++)

{

BigDecimal t = a[j][k]; a[j][k] = a[imax][k]; a[imax][k] = t;

}

BigDecimal t = scaling[imax]; scaling[imax] = scaling[j]; scaling[j] = t;

sign = -sign;

}

if (j != n-1)

for (int i=j+1; i<n; i++) a[i][j] = a[i][j].divide

(a[j][j], 100,

BigDecimal.ROUND_HALF_EVEN);

}

BigDecimal result = new BigDecimal (1); if (sign == -1)

result = result.negate(); for (int i=0; i<n; i++)

result = result.multiply (a[i][i]);

return result.divide

(BigDecimal.valueOf(1), 0, BigDecimal. ROUND_HALF_EVEN).toBigInteger();

}

catch (Exception e)

{

return BigInteger.ZERO;

}

}

Интегрирование по формуле Симпсона

Требуется посчитать значение определённого интеграла:

Решение, описываемое здесь, было опубликовано в одной из диссертаций Томаса Симпсона (Thomas Simpson)

в 1743 г.

Формула Симпсона

Пусть — некоторое натуральное число. Разобьём отрезок интегрирования на равных частей:

Её можно найти аналитически, затем останется только проинтегрировать выражение для неё, и окончательно получаем:

Складывая эти значения по всем отрезкам, получаем окончательную формулу Симпсона:

Погрешность

Погрешность, даваемая формулой Симпсона, не превосходит по модулю величины:

Таким образом, погрешность имеет порядок уменьшения как .

Реализация

Здесь — некоторая пользовательская функция.

double a, b; // входные данные

const int N = 1000*1000; // количество шагов (уже умноженное на 2) double s = 0;

double h = (b - a) / N; for (int i=0; i<=N; ++i) {

double x = a + h * i;

s += f(x) * ((i==0 || i==N) ? 1 : ((i&1)==0) ? 2 : 4);

}

s *= h / 3;

Метод Ньютона (касательных) для поиска корней

Это итерационный метод, изобретённый Исааком Ньютоном (Isaak Newton) около 1664 г. Впрочем, иногда этот метод называют методом Ньютона-Рафсона (Raphson), поскольку Рафсон изобрёл тот же самый алгоритм

на несколько лет позже Ньютона, однако его статья была опубликована намного раньше. Задача заключается в следующем. Дано уравнение:

Требуется решить это уравнение, точнее, найти один из его корней (предполагается, что корень существует). Предполагается, что непрерывна и дифференцируема на отрезке .

Алгоритм

Входным параметром алгоритма, кроме функции , является также начальное приближение — некоторое , от которого алгоритм начинает идти.

точке , и найдём точку пересечения этой касательной с осью абсцисс. положим равным найденной точке, и повторим весь процесс с начала.

Нетрудно получить следующую формулу:

то будет находиться ещё ближе к искомому корню.

Скорость сходимости является квадратичной, что, условно говоря, означает, что число точных разрядов в приближенном значении удваивается с каждой итерацией.

Применение для вычисления квадратного корня

Рассмотрим метод Ньютона на примере вычисления квадратного корня. Если подставить , то после упрощения выражения получаем:

Первый типичный вариант задачи — когда дано дробное число , и нужно подсчитать его корень с некоторой точностью :

double n; cin >> n;

const double EPS = 1E-15; double x = 1;

for (;;) {

double nx = (x + n / x) / 2; if (abs (x - nx) < EPS) break; x = nx;

}

printf ("%.15lf", x);

Другой распространённый вариант задачи — когда требуется посчитать целочисленный корень (для данного найти наибольшее такое, что ). Здесь приходится немного изменять условие останова алгоритма,

поскольку может случиться, что начнёт "скакать" возле ответа. Поэтому мы добавляем условие, что если значение на предыдущем шаге уменьшилось, а на текущем шаге пытается увеличиться, то алгоритм надо остановить.

int n; cin >> n;