e-maxx_algo

алгоритм построения Z-функции строки, который внутренне сильно напоминает данный алгоритм, и работает также

за линейное время.)

В самом деле, легко проследить по алгоритму, что каждая итерация, производимая тривиальным поиском, приводит к увеличению на один границы . При этом уменьшений по ходу алгоритма происходить не может. Следовательно, тривиальный алгоритм в сумме совершит лишь действий.

Учитывая, что, кроме тривиальных поисков, все остальные части алгоритма Манакера очевидно работают за линейное время, мы и получаем итоговую асимптотику: .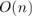

Реализация алгоритма Манакера

Для случая подпалиндромов нечётной длины, т.е. для вычисления массива , получаем такой код:

vector<int> d1 (n); int l=0, r=-1;

for (int i=0; i<n; ++i) {

vector<int> d2 (n); l=0, r=-1;

for (int i=0; i<n; ++i) {

int k = (i>r ? 0 : min (d2[l+r-i+1], r-i+1)) + 1;

while (i+k-1 < n && i-k >= 0 && s[i+k-1] == s[i-k]) ++k; d2[i] = --k;

if (i+k-1 > r)

l = i-k, r = i+k-1;

}

Задачи в online judges

Список задач, которые можно сдать с использованием этого алгоритма:

● UVA #11475 "Extend to Palindrome" [сложность: низкая]

Декомпозиция Линдона. Алгоритм Дюваля. Нахождение наименьшего циклического сдвига

Понятие декомпозиции Линдона

Определим понятие декомпозиции Линдона (Lyndon decomposition).

Строка называется простой, если она строго меньше любого своего собственного суффикса. Примеры простых строк: , , , , , , . Можно показать, что строка является простой тогда и только тогда, когда она строго меньше всех своих нетривиальных циклических сдвигов.

Можно показать, что для любой строки это разложение существует и единственно.

Алгоритм Дюваля

Алгоритм Дюваля (Duval's algorithm) находит для данной строки длины декомпозицию Линдона за время

с использованием дополнительной памяти. Работать со строками будем в 0-индексации.

Введём вспомогательное понятие предпростой строки. Строка называется предпростой, если она имеет вид , где — некоторая простая строка, а — некоторый префикс строки .

Алгоритм Дюваля является жадным. В любой момент его работы строка S фактически разделена на три строки , где в строке декомпозиция Линдона уже найдена и уже больше не используется

алгоритмом; строка — это предпростая строка (причём длину простых строк внутри неё мы также запоминаем); строка — это ещё не обработанная часть строки . Каждый раз алгоритм Дюваля берёт первый символ строки 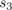и пытается дописать его к строке . При этом, возможно, для какого-то префикса строки декомпозиция Линдона становится известной, и эта часть переходит к строке .

на простые строки плюс "остаток" (префикс простой строки, возможно, пустой); простые строки добавляем в ответ (т. е. выводим их позиции, попутно передвигая указатель ), а "остаток" вместе с символом переводим обратно в

строку , и останавливаем выполнение внутреннего цикла. Тем самым мы на следующей итерации внешнего цикла заново обработаем остаток, зная, что он не мог образовать предпростую строку с предыдущими простыми строками. Осталось только заметить, что при выводе позиций простых строк нам нужно знать их длину; но она, очевидно, равна .

Реализация

Приведём реализацию алгоритма Дюваля, которая будет выводить искомую декомпозицию Линдона строки :

string s; // входная строка int n = (int) s.length(); int i=0;

while (i < n) {

int j=i+1, k=i;

while (j < n && s[k] <= s[j]) { if (s[k] < s[j])

k = i;

else

++k;

++j;

}

while (i <= k) {

cout << s.substr (i, j-k) << ' '; i += j - k;

}

}

Асимптотика

Сразу заметим, что для алгоритма Дюваля требуется памяти, а именно три указателя , , . Оценим теперь время работы алгоритма.

Внешний цикл while делает не более итераций, поскольку в конце каждой его итерации выводится как минимум один символ (а всего символов выводится, очевидно, ровно ).

Оценим теперь количество итераций первого вложенного цикла while. Для этого рассмотрим

символов, получаем, что для вывода символов требуется не более итераций первого вложенного while-а.

Следовательно, алгоритм Дюваля выполняется за .

Легко оценить и число сравнений символов, выполняемых алгоритмом Дюваля. Поскольку каждая итерация первого вложенного цикла while производит два сравнения символов, а также одно сравнение производится после последней итерации цикла (чтобы понять, что цикл должен остановиться), то общее число сравнений символов не превосходит .

Нахождение наименьшего циклического сдвига

и памяти (если не выполнять конкатенацию в явном виде)). Найдём предпростой блок, который начинается

в позиции, меньшей (т.е. в первом экземпляре строки ), и заканчивается в позиции, большей или равной n (т.е. во втором экземпляре). Утверждается, что позиция начала этого блока и будет началом искомого циклического сдвига (в этом легко убедиться, воспользовавшись определением декомпозиции Линдона).

Начало предпростого блока найти просто — достаточно заметить, что указатель в начале каждой итерации внешнего цикла while указывает на начало текущего предпростого блока.

else

++k;

++j;

}

while (i <= k) i += j - k;

}

return s.substr (ans, n/2);

}

Задачи в online judges

Список задач, которые можно решить, используя алгоритм Дюваля: ● UVA #719 "Glass Beads" [сложность: низкая]

Алгоритм Ахо-Корасик

Пусть дан набор строк в алфавите размера суммарной длины . Алгоритм Ахо-Корасик строит для этого набора строк структуру данных "бор", а затем по этому бору строит автомат, всё за времени и

памяти. Полученный автомат уже может использоваться в различных задачах, простейшая из которых — это нахождение всех вхождений каждой строки из данного набора в некоторый текст за линейное время.

Данный алгоритм был предложен канадским учёным Альфредом Ахо (Alfred Vaino Aho) и учёным Маргарет Корасик (Margaret John Corasick) в 1975 г.

Бор. Построение бора

Формально, бор — это дерево с корнем в некоторой вершине , причём каждое ребро дерево подписано некоторой буквой. Если мы рассмотрим список рёбер, выходящих из данной вершины (кроме ребра, ведущего в предка), то все рёбра должны иметь разные метки.

Рассмотрим в боре любой путь из корня; выпишем подряд метки рёбер этого пути. В результате мы получим некоторую строку, которая соответствует этому пути. Если же мы рассмотрим любую вершину бора, то ей поставим в соответствие строку, соответствующую пути из корня до этой вершины.

Каждая вершина бора также имеет флаг , который равен , если в этой вершине оканчивается какая-либо строка из данного набора.

Опишем теперь, как построить бор по заданному набору строк за линейное время относительно их суммарной длины.

Введём структуру, соответствующую вершинам бора:

struct vertex {

int next[K]; bool leaf;

};

vertex t[NMAX+1]; int sz;

в которую ведёт ребро по символу , или , если такого ребра нет.

Вначале бор состоит только из одной вершины — корня (договоримся, что корень всегда имеет в массиве индекс ). Поэтому инициализация бора такова:

memset (t[0].next, 255, sizeof t[0].next); sz = 1;

Теперь реализуем функцию, которая будет добавлять в бор заданную строку . Реализация крайне проста:

void add_string (const string & s) { int v = 0;

for (size_t i=0; i<s.length(); ++i) {

char c = s[i]-'a'; // в зависимости от алфавита if (t[v].next[c] == -1) {

memset (t[sz].next, 255, sizeof t[sz].next); t[v].next[c] = sz++;

}

v = t[v].next[c];

}

t[v].leaf = true;

}

Линейное время работы, а также линейное количество вершин в боре очевидны. Поскольку на каждую вершину приходится памяти, то использование памяти есть .

до . Для этого достаточно хранить переходы 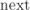не массивом, а отображением .

Построение автомата

Пусть мы построили бор для заданного набора строк. Посмотрим на него теперь немного с другой стороны. Если мы рассмотрим любую вершину, то строка, которая соответствует ей, является префиксом одной или нескольких строк из набора; т.е. каждую вершину бора можно понимать как позицию в одной или нескольких строках из набора.

Т.е. мы можем понимать рёбра бора как переходы в автомате по соответствующей букве. Однако одними только рёбрами бора нельзя ограничиваться. Если мы пытаемся выполнить переход по какой-либо букве, а соответствующего ребра в боре нет, то мы тем не менее должны перейти в какое-то состояние.

Более строго, пусть мы находимся в состоянии , которому соответствует некоторая строка , и хотим выполнить переход по символу . Если в боре из вершины есть переход по букве , то мы просто переходим по этому ребру и попадаем в вершину, которой соответствует строка . Если же такого ребра нет, то мы должны найти состояние, соответствующее наидлиннейшему собственному суффиксу строки (наидлиннейшему из имеющихся в боре), и попытаться выполнить переход по букве из него.

бора; для удобства суффиксную ссылку из него проведём в себя же. Теперь мы можем переформулировать утверждение по поводу переходов в автомате так: пока из текущей вершины бора нет перехода по соответствующей букве (или пока мы не придём в корень бора), мы должны переходить по суффиксной ссылке.

Таким образом, мы свели задачу построения автомата к задаче нахождения суффиксных ссылок для всех вершин бора. Однако строить эти суффиксные ссылки мы будем, как ни странно, наоборот, с помощью построенных в автомате переходов.

Заметим, что если мы хотим узнать суффиксную ссылку для некоторой вершины , то мы можем перейти в предка

текущей вершины (пусть — буква, по которой из есть переход в ), затем перейти по его суффиксной ссылке, а затем из неё выполнить переход в автомате по букве .

Таким образом, задача нахождения перехода свелась к задаче нахождения суффиксной ссылки, а задача нахождения суффиксной ссылки — к задаче нахождения суффиксной ссылки и перехода, но уже для более близких к корню вершин. Мы получили рекурсивную зависимость, но не бесконечную, и, более того, разрешить которую можно за линейное время.

Перейдём теперь к реализации. Заметим, что нам теперь понадобится для каждой вершины хранить её предка , а также символ , по которому из предка есть переход в нашу вершину. Также в каждой вершине будем

в автомате по каждому из символов (опять же, если элемент массива равен , то он ещё не вычислен). Приведём теперь полную реализацию всех необходимых функций:

struct vertex {

int next[K]; bool leaf; int p;

char pch; int link; int go[K];

};

vertex t[NMAX+1]; int sz;

void init() {

t[0].p = t[0].link = -1;

memset (t[0].next, 255, sizeof t[0].next); memset (t[0].go, 255, sizeof t[0].go);

sz = 1;

}

void add_string (const string & s) { int v = 0;

for (size_t i=0; i<s.length(); ++i) { char c = s[i]-'a';

if (t[v].next[c] == -1) {

memset (t[sz].next, 255, sizeof t[sz].next); memset (t[sz].go, 255, sizeof t[sz].go); t[sz].link = -1;

t[sz].p = v; t[sz].pch = c; t[v].next[c] = sz++;

}

v = t[v].next[c];

}

t[v].leaf = true;

}

int go (int v, char c);

int get_link (int v) {

if (t[v].link == -1)

if (v == 0 || t[v].p == 0) t[v].link = 0;

else

t[v].link = go (get_link (t[v].p), t[v].pch); return t[v].link;

}

int go (int v, char c) {

if (t[v].go[c] == -1)

if (t[v].next[c] != -1) t[v].go[c] = t[v].next[c];

else

t[v].go[c] = v==0 ? 0 : go (get_link (v), c); return t[v].go[c];

}

Нетрудно понять, что, за счёт запоминания найденных суффиксных ссылок и переходов, суммарное время нахождения всех суффиксных ссылок и переходов будет линейным.

Применения

Поиск всех строк из заданного набора в тексте

Дан набор строк, и дан текст. Требуется вывести все вхождения всех строк из набора в данный текст за время , где — длина текста, — размер ответа.

Построим по данному набору строк бор. Будем теперь обрабатывать текст по одной букве, перемещаясь соответствующим образом по дереву, фактически — по состояниям автомата. Изначально мы находимся в корне дерева. Пусть мы на очередном шаге мы находимся в состоянии , и очередная буква текста . Тогда следует переходить в состояние , тем самым либо увеличивая на длину текущей совпадающей подстроки,

либо уменьшая её, проходя по суффиксной ссылке.

Как теперь узнать по текущему состоянию , имеется ли совпадение с какими-то строками из набора? Во-первых, понятно, что если мы стоим в помеченной вершине ( ), то имеется совпадение с тем образцом, который в боре оканчивается в вершине . Однако это далеко не единственный возможный случай достижения совпадения: если мы, двигаясь по суффиксным ссылкам, мы можем достигнуть одной или нескольких помеченных вершин, то совпадение также будет, но уже для образцов, оканчивающихся в этих состояниях. Простой пример такой ситуации

— когда набор строк — это , а текст — это .

Таким образом, если в каждой помеченной вершине хранить номер образца, оканчивающегося в ней (или список

номеров, если допускаются повторяющиеся образцы), то мы можем для текущего состояния за найти номера

всех образцов, для которых достигнуто совпадение, просто пройдя по суффиксным ссылкам от текущей вершины до корня. Однако это недостаточно эффективное решение, поскольку в сумме асимптотика получится .

Однако можно заметить, что движение по суффиксным ссылкам можно соптимизировать, предварительно посчитав для каждой вершины ближайшую к ней помеченную вершину, достижимую по суффиксным ссылкам (это называется "функцией выхода"). Эту величину можно считать ленивой динамикой за линейное время. Тогда для

В более простом случае, когда надо найти не сами вхождения, а только их количество, можно вместо функции выхода посчитать ленивой динамикой количество помеченных вершин, достижимых из текущей вершины

самым, задача нахождения суммарного количества вхождений может быть решена нами за .

Нахождение лексикографически наименьшей строки данной длины, не содержащей ни один из данных образцов

Дан набор образцов, и дана длина . Требуется найти строку длины , не содержащую ни один из образцов, и из всех таких строк вывести лексикографически наименьшую.

Построим по данному набору строк бор. Вспомним теперь, что те вершины, из которых по суффиксным ссылкам можно достичь помеченных вершин (а такие вершины можно найти за , например, ленивой динамикой),

можно воспринимать как вхождение какой-либо строки из набора в заданный текст. Поскольку в данной задаче нам необходимо избегать вхождений, то это можно понимать как то, что в такие вершины нам заходить нельзя. С другой стороны, во все остальные вершины мы заходить можем. Таким образом, мы удаляем из автомата все

"плохие" вершины, а в оставшемся графе автомата требуется найти лексикографически наименьший путь длины . Эту задачу уже можно решить за , например, поиском в глубину.

Нахождение кратчайшей строки, содержащей вхождения одновременно всех образцов

Снова воспользуемся той же идеей. Для каждой вершины будем хранить маску, обозначающую образцы, для которых произошло вхождение в данной вершине. Тогда задачу можно переформулировать так: изначально находясь в состоянии , требуется дойти до состояния , где —

количество образцов. Переходы из состояния в состояние будут представлять собой добавление одной буквы к тексту, т. е. переход по ребру автомата в другую вершину с соответствующим изменением маски. Запустив обход в ширину на

таком графе, мы найдём путь до состояния наименьшей длины, что нам как раз и требовалось.

Нахождение лексикографически наименьшей строки длины

, содержащей данные образцы в сумме раз

Как и в предыдущих задачах, посчитаем для каждой вершины количество вхождений, которое соответствует ей (т. е. количество помеченных вершин, достижимых из неё по суффиксным ссылкам). Переформулируем задачу

— это просто переходы по рёбрам автомата из текущей вершины. Таким образом, достаточно просто найти обходом в глубину путь между этими двумя состояниями (если обход в глубину будет просматривать буквы в их естественном порядке, то найденный путь автоматически будет лексикографически наименьшим).

Задачи в online judges

Задачи, которые можно решить, используя бор или алгоритм Ахо-Корасик: ● UVA #11590 "Prefix Lookup" [сложность: низкая]

● UVA #11171 "SMS" [сложность: средняя]

● UVA #10679 "I Love Strings!!!" [сложность: средняя]

Суффиксное дерево. Алгоритм Укконена

Эта статья — временная заглушка, и не содержит никаких описаний.

Описание алгоритма Укконена можно найти, например, в книге Гасфилда "Строки, деревья и последовательности в алгоритмах".

Реализация алгоритма Укконена

Входными данными для алгоритма являются строка и её длина , которые передаются в виде глобальных переменных.

else {

if (s[ t[st.v].l + st.pos ] != s[l]) return state (-1, -1);

if (r-l < t[st.v].len() - st.pos)

return state (st.v, st.pos + r-l); l += t[st.v].len() - st.pos;

st.pos = t[st.v].len();

}

return st;

}

int split (state st) {

if (st.pos == t[st.v].len()) return st.v;

if (st.pos == 0)

return t[st.v].par; node v = t[st.v];

int id = sz++;

t[id] = node (v.l, v.l+st.pos, v.par); t[v.par].get( s[v.l] ) = id; t[id].get( s[v.l+st.pos] ) = st.v; t[st.v].par = id;

t[st.v].l += st.pos; return id;

}

int get_link (int v) {

if (t[v].link != -1) return t[v].link; if (t[v].par == -1) return 0;

int to = get_link (t[v].par);

return t[v].link = split (go (state(to,t[to].len()), t[v].l + (t [v].par==0), t[v].r));

}

void tree_extend (int pos) { for(;;) {

state nptr = go (ptr, pos, pos+1); if (nptr.v != -1) {

ptr = nptr; return;

}

int mid = split (ptr); int leaf = sz++;

t[leaf] = node (pos, n, mid); t[mid].get( s[pos] ) = leaf;

ptr.v = get_link (mid); ptr.pos = t[ptr.v].len(); if (!mid) break;

}

}

void build_tree() { sz = 1;

for (int i=0; i<n; ++i) tree_extend (i);

}

Сжатая реализация

Приведём также следующую компактную реализацию алгоритма Укконена, предложенную freopen:

const int N=1000000,INF=1000000000; string a;

int t[N][26],l[N],r[N],p[N],s[N],tv,tp,ts=2;

void ukkadd (int c) { suff:;

if (r[tv]<tp) {

if (t[tv][c]==-1) { t[tv][c]=ts; l[ts]=a.size()-1; r[ts]=INF; p[ts++]=tv; tv=s[tv]; tp=r[tv]+1; goto suff; }

tv=t[tv][c]; tp=l[tv];

}

if (tp==-1 || c==a[tp]) tp++; else { l[ts+1]=a.size()-1; r[ts+1]=INF; p[ts+1]=ts;

l[ts]=l[tv]; r[ts]=tp-1; p[ts]=p[tv]; t[ts][c]=ts+1; t[ts]

[a[tp]]=tv;

l[tv]=tp; p[tv]=ts; t[p[ts]][a[l[ts]]]=ts; ts+=2; tv=s[p[ts-2]]; tp=l[ts-2];

while (tp<=r[ts-2]) { tv=t[tv][a[tp]]; tp+=r[tv]-l[tv]+1;}