
Кожевников. Матрицы и СЛУ
.pdf
30
•ãáâì ¬ë 㦥 ¯®«ã稫¨ (á¬. ¯à¥¤ë¤ã騩 «£®à¨â¬) áâ㯥-ç - âãî ¬ âà¨æã A = (aij) 2 Mm£n, ¢ ª®в®а®© -¥-г«¥¢л¬¨ п¢«повбп
¯¥à¢ë¥ r áâப, a1j1 ; a2j2 ; : : : ; arjr | ¢¥¤ã騥 í«¥¬¥-âë íâ¨å áâப
(j1 < j2 < : : : < jr), ¯à¨ç¥¬ a1j1 = a2j2 = : : : = arjr = 1.
‚믮«-ïï |
¯®á«¥¤®¢ ⥫ì-® |
T1r(¡a1jr ), T2r(¡a2jr ), |
: : : ; |
||||||||
Tr¡1 r(¡ar¡1 jr ) |
(íâ® è £ |
®¡à â-®£® |
室 |
¬¥â®¤ |
ƒ ãáá ), |
¯à¥- |
|||||
¢à é ¥¬ ¢ 0 ¢á¥ í«¥¬¥-âë |
jr |
-£® á⮫¡æ , § |
¨áª«îç¥-¨¥¬ |
arjr |
= 1 |
. |
|||||
e |
|
|
e |
|
|
e |
|
|
|||
•à¨ í⮬ ¬ âà¨æ ®áâ ¥âáï áâ㯥-ç ⮩. |
|
|
|
|
|
|
|||||
„ «¥¥ ¯®á«¥¤®¢ ⥫ì-® ¯à®¨§¢®¤¨¬ |
|
- «®£¨ç-ë¥ ¤¥©áâ¢¨ï ¤«ï |
|||||||||
jr¡1-£®, . . . , j2-£® á⮫¡æ®¢. |
|
|
|
|
|
|
|
|
|
|
|
ˆв ª, ¬л ª®-бвагªв¨¢-® ¤®ª § «¨ б«¥¤гойго в¥®а¥¬г.
’¥®à¥¬ 4.1. Œ âà¨æ A 2 Mm£n ¬®¦¥â ¡ëâì ¯à¨¢¥¤¥- í«¥- ¬¥-â à-묨 ¯à¥®¡à §®¢ -¨ï¬¨ áâப 1) ª áâ㯥-ç ⮬㠢¨¤ã; 2) ª ã¯à®é¥--®¬ã ¢¨¤ã.
•«¥¬¥-â à-ë¥ ¯à¥®¡à §®¢ -¨ï ¨ à -£
•ãáâì ¬ âà¨æ A = (a²1 : : : a²n) ¯®á«¥ -¥ª®â®à®£® í«¥¬¥-â à-®£® ¯à¥®¡à §®¢ -¨ï áâப ¯¥à¥è« ¢ ¬ âà¨æã A0 = (a0²1 : : : a0²n). •ãáâì -¥ª®â®à ï «¨-¥©- ï ª®¬¡¨- æ¨ï á⮫¡æ®¢ a²j1 , : : : ; a²jl à ¢- O:
P |
l |
sP |
l |
|
l |
¸sa²js = O, â® ¥áâì |
¸saijs = 0 ¤«ï ¢á¥å i. ’®£¤ , ª ª -¥âàã¤-® |
||
s=1 |
|
|
=1 |
殢 a²0 j1 ,sP: : : ; a²0 jl |
á ⥬¨ ¦¥ ª®íää¨æ¨¥-â ¬¨ ¸1; : : : ; ¸l à ¢- O. ˆ§ |
||
¢¨¤¥âì, =1 |
ijs |
= 0 ¤«ï ¢á¥å i, â® ¥áâì «¨-¥©- ï ª®¬¡¨- æ¨ï á⮫¡- |
|
|
¸sa0 |
||
í⮣® á®®¡à ¦¥-¨ï ¢ë⥪ ¥â
•à¥¤«®¦¥-¨¥ 4.4. •ãáâì 1 6 j1 < j2 < : : : < jl 6 n. •à¨ í«¥¬¥--
â à-ëå ¯à¥®¡à §®¢ -¨ïå áâப ¬ âà¨æë A 2 Mm£n á®åà -ï¥âáï «¨-¥©- ï § ¢¨á¨¬®áâì ¨«¨ -¥§ ¢¨á¨¬®áâì á¨á⥬ë á⮫¡æ®¢ á -®-
¬¥à ¬¨ j1; j2; : : : ; jl.
B •ãáâì ¬ âà¨æ A = (a²1 : : : a²n) ¯®á«¥ -¥ª®â®à®£® í«¥¬¥-â à- -®£® ¯à¥®¡à §®¢ -¨ï áâப ¯¥à¥è« ¢ ¬ âà¨æã A0 = (a0²1 : : : a0²n).
…᫨ ¯®¤á¨á⥬ á⮫¡æ®¢ a²j1 , : : : ; a²jl ¬ âà¨æë A 2 Mm£n «¨- -¥©-® § ¢¨á¨¬ , â®, ª ª ¯®ª § -® ¢ëè¥, ¯®¤á¨á⥬ á⮫¡æ®¢ a0²j1 ,
: : : ; a0²jl â ª¦¥ «¨-¥©-® § ¢¨á¨¬ .

B ‘à §ã á«¥¤ã¥â ¨§ ¯à¥¤ë¤ã饣® ¯à¥¤«®¦¥-¨ï. ¤
‘«¥¤á⢨¥. •ãáâì A | áâ㯥-ç â ï ¬ âà¨æ , ¢ ª®â®à®© ஢-® r -¥-ã«¥¢ëå áâப. ’®£¤ rgv A = r.
B•ãáâì ¯®á«¥ 㤠«¥-¨ï -ã«¥¢ëå áâப ¨§ ¬ âà¨æë A ¯®«ãç ¥âáï
¬âà¨æ A0. ‘ ¯®¬®éìî ®¡à â-®£® 室 ¬¥â®¤ ƒ ãáá ¨§ A0 ¬®¦-®
¯®«ãç¨âì ¬ âà¨æã ã¯à®é¥--®£® ¢¨¤ B, ¨¬¥îéãî ¯®¤¬ âà¨æã Er
(á¬. «£®à¨â¬). 0 ˆá¯®«ì§ãï0 ¯à¥¤«®¦¥-¨ï 4.5, 2.8 ¨ 2.4, ¯®«ãç ¥¬,
çâ® rgv A = rgv A , r > rgv A = rgv B > rgv Er = r. ¤
•à¥¤«®¦¥-¨¥ 4.6. ‘âà®ç-ë© à -£ ¬ âà¨æë -¥ ¨§¬¥-ï¥âáï ¯à¨ í«¥¬¥-â à-ëå ¯à¥®¡à §®¢ -¨ïå áâப.
B „«ï í«¥¬¥-â à-®£® ¯à¥®¡à §®¢ -¨ï áâப I ⨯ íâ® ïá-®, â ª
ª ª -¥ ¬¥-ï¥âáï - ¡®à áâப.
Š ª á«¥¤ã¥â ¨§ ⥮६ë 2.1, ¯à¨ í«¥¬¥-â à-®¬ ¯à¥®¡à §®¢ -¨¨ II ⨯ à -£ á¨á⥬ë áâப -¥ 㢥«¨ç¨¢ ¥âáï: rg(a1 ²; : : : ; ¸ai ²; : : :
: : : ; am ²) 6 rg(a1 ²; : : : ; ai ²; : : : ; am ²; ¸ai ²) = rg(a1 ²; : : : ; ai ²; : : : ; am ²): rg(a1 ²; : : :
: : : ; ai ² + ¸aj²; : : : ; am ²) 6 rg(a1 ²; : : : ; ai ²; : : : ; am ²; ai ² + ¸aj²) =
= rg(a1 ²; : : : ; ai ²; : : : ; am ²):
•® à áᬠâਢ ï ®¡à â-®¥ í«¥¬¥-â à-®¥ ¯à¥®¡à §®¢ -¨¥, ¯®«ã- ç ¥¬, çâ® à -£ ¨ -¥ 㬥-ìè¨âáï. ¤
’¥®à¥¬ 4.2 (® à -£¥ ¬ âà¨æë). „«ï «î¡®© ¬ âà¨æë A 2 Mm£n
¢ë¯®«-¥-® rgv A = rgh A.
B „®ª ¦¥¬ ¢- ç «¥, çâ® ¤«ï «î¡®© ¬ âà¨æë rgv A > rgh A. •«¥¬¥-â à-묨 ¯à¥®¡à §®¢ -¨ï¬¨ áâப ¯à¨¢¥¤¥¬ A ª áâ㯥-ç -
⮬㠢¨¤ã A0, ¨ ¯ãáâì ¢ A0 ஢-® r -¥-ã«¥¢ëå áâப. ’®£¤ rgh A0 6 r,

32 |
|
rgv |
A0 = r (á¬. ¯à¥¤ë¤ã饥 á«¥¤á⢨¥). ˆ§ á®åà -¥-¨ï à -£®¢ ¯à¨ |
í«¥¬¥-â à-ëå ¯à¥®¡à §®¢ -¨ïå (¯à¥¤«®¦¥-¨ï 4.5 ¨ 4.6) á«¥¤ã¥â, çâ® |
|
rgv |
A = rgv A0 ¨ rgh A = rgh A0, ®âªã¤ rgv A = r > rgh A. |
‚®á¯®«ì§®¢ ¢è¨áì ¤®ª § --ë¬ -¥à ¢¥-á⢮¬ ¤«ï AT , ¨¬¥¥¬
rgh A = rgv(AT ) > rgh(AT ) = rgv A. ¤
’¥¯¥àì ¢¬¥áâ® rgv A ¨ rgh A ¬ë ¨á¯®«ì§ã¥¬ ®¤-® ®¡®§- ç¥-¨¥ rg A.
‘«¥¤á⢨¥. „«ï «î¡®© ¬ âà¨æë A ¢ë¯®«-¥-® rg A = rg AT .
ˆ§ ¤®ª § --®£® ¢ë⥪ ¥â
€‹ƒŽ•ˆ’Œ - 宦¤¥-¨ï à -£ ¬ âà¨æë ¨ -¥ª®â®à®© ¡ §¨á-®© ¯®¤á¨á⥬ë á⮫¡æ®¢.32
„ --ãî ¬ âà¨æã A ¯à¨¢¥¤¥¬ í«¥¬¥-â à-묨 ¯à¥®¡à §®¢ -¨ï¬¨ áâப ª áâ㯥-ç ⮬㠢¨¤ã A0 (¬¥â®¤®¬ ƒ ãáá ).
•ãáâì ¢ A0 ஢-® r -¥-ã«¥¢ëå áâப (r "áâ㯥-¥ª"), ¨ j1 < j2 < : : :
: : : < jr | -®¬¥à á⮫¡æ®¢, ᮤ¥à¦ é¨å ¢¥¤ã騥 í«¥¬¥-âë áâப. ’®£¤ rg A = r, á⮫¡æë ¬ âà¨æë A á -®¬¥à ¬¨ j1, j2, . . . , jr
п¢«повбп ¡ §¨б-®© ¯®¤б¨бв¥¬®© бв®«¡ж®¢ ¬ ва¨жл A.
„¥©á⢨⥫ì-®, ¢ ¤®ª § ⥫ìá⢥ â¥®à¥¬ë ® à -£¥ ¬ âà¨æë ¬ë ¯®«ã稫¨, çâ® à -£ à ¢¥- ª®«¨ç¥áâ¢ã -¥-ã«¥¢ëå áâப ¯®á«¥ ¯à¨¢¥- ¤¥-¨ï ª áâ㯥-ç ⮬㠢¨¤ã. ‚ áâ㯥-ç ⮬ (¨ ¢ ã¯à®é¥--®¬) ¢¨¤¥ á⮫¡æë á -®¬¥à ¬¨ j1, j2, . . . , jr ®¡à §ãîâ ¡ §¨á-ãî ¯®¤á¨á⥬ã,
⮣¤ (á¬. ¯à¥¤«®¦¥-¨¥ 4.4) ¨ ¢ ¨á室-®© ¬ âà¨æ¥ A á¨á⥬ á⮫¡- 殢 á -®¬¥à ¬¨ j1; j2; : : : ; jr ï¥âáï ¡ §¨á-®©.
•¥¢ë஦¤¥--ë¥ ¬ âà¨æë
Ž¯à¥¤¥«¥-¨¥. Š¢ ¤à â- ï ¬ âà¨æ A 2 Mn£n - §ë¢ ¥âáï -¥- ¢ë஦¤¥--®©, ¥á«¨ rg A = n, ¨ ¢ë஦¤¥--®© ¢ ¯à®â¨¢-®¬ á«ãç ¥.
ˆ- ç¥ £®¢®àï, ¢ -¥¢ë஦¤¥--®© ¬ âà¨æ¥ á¨á⥬ ¢á¥å á⮫¡æ®¢ (¨«¨ áâப) «¨-¥©-® -¥§ ¢¨á¨¬ .
32Š®-¥ç-®, ¢ á¨á⥬¥ á⮫¡æ®¢ ¬®¦¥â ¡ëâì -¥ ¥¤¨-á⢥-- ï ¡ §¨á- ï ¯®¤á¨á- ⥬ .

33
’¥®à¥¬ 4.3 (ªà¨â¥à¨© -¥¢ë஦¤¥--®áâ¨-1). „«ï ª¢ ¤à â-®© ¬ âà¨æë A 2 Mn£n á«¥¤ãî騥 ãá«®¢¨ï íª¢¨¢ «¥-â-ë:
1) A | -¥¢ë஦¤¥-- ï;
2) A ¯à¨¢®¤¨âáï í«¥¬¥-â à-묨 ¯à¥®¡à §®¢ -¨ï¬¨ áâப ª ¥¤¨-
-¨ç-®© ¬ âà¨æ¥ En;
3) A à ¢- ¯à®¨§¢¥¤¥-¨î -¥áª®«ìª¨å í«¥¬¥-â à-ëå ¬ âà¨æ; 4) A | ®¡à ⨬ ï;
5) A | ®¡à ⨬ ï á«¥¢ ; 5') A | ®¡à ⨬ ï á¯à ¢ .
B 5) (¨«¨ 5')) ) 1) …᫨ BA = E (¨«¨ AC = E), â® ¨§ ¯à¥¤«®- ¦¥-¨ï 3.3 ® à -£¥ ¯à®¨§¢¥¤¥-¨ï ¨¬¥¥¬: rg A > rg E = n.
1) |
) |
2) •à¨¢¥¤¥¬ A ª ã¯à®é¥--®¬ã ¢¨¤ã A0. ’ ª ª ª rg A0 = |
||||
|
|
|
¤®«¦- ᮤ¥à¦ âì ¥¤¨-¨ç-ãî ¯®¤¬ âà¨æã ¯®à浪 |
|||
= rg A = n, â® A0 |
|
|
|
|||
n, §- ç¨â, A0 = E. |
|
|
||||
2) |
) 3) ˆ§ 2) ¨ ¯à¥¤«®¦¥-¨ï 4.2 á«¥¤ã¥â à ¢¥-á⢮ SkSk¡1 : : : |
|||||
: : : S1A = E, £¤¥ Si | í«¥¬¥-â à-ë¥ ¬ âà¨æë. ’®£¤ |
¤®¬-®¦ ï íâ® |
|||||
à ¢¥-á⢮ á«¥¢ |
¯®á«¥¤®¢ ⥫ì-® - í«¥¬¥-â à-ë¥ ¬ âà¨æë Sk¡1; : : : ; |
|||||
S¡1 |
|
|
|
|
A = S¡1S¡1 : : : S¡1 |
|
1 (á¬. ¯à¥¤«®¦¥-¨¥ 4.3), ¯®«ã稬 |
1 2 |
k . |
||||
3) ) 4) ‚ë⥪ ¥â ¨§ ⥮६ë 3.2 (¯à®¨§¢¥¤¥-¨¥ ®¡à ⨬ëå ¬ â-
à¨æ | ®¡à ⨬ ï ¬ âà¨æ ).
4) ) 5) (¨«¨ 5')) Žç¥¢¨¤-®. ¤
•à¥¤«®¦¥-¨¥ 4.7. •ãáâì
2 Mn£p. •ãáâì (¡«®ç- ï) ¬ âà¨æ (A B) 2 Mn£(n+p) ¯à¨¢¥¤¥-
í«¥¬¥-â à-묨 ¯à¥®¡à §®¢ -¨ï¬¨ áâப ª ¢¨¤ã (En C). ’®£¤ C =
= A¡1B.
B ‚믮«-¥-¨¥ í«¥¬¥-â à-ëå ¯à¥®¡à §®¢ -¨© íª¢¨¢ «¥-â-® ¤®-
¬-®¦¥-¨î á«¥¢ - -¥ª®â®àãî (®¡à ⨬ãî) ¬ âà¨æã R 2 Mn£n (á¬. ¯à¥¤«®¦¥-¨¥ 4.2): (E C) = R(A B). ’®£¤ RA = E, RB = C ) R =
= A¡1 ¨ C = A¡1B. ¤
•®á«¥¤-¥¥ ¯à¥¤«®¦¥-¨¥ ¤ ¥â, ¢ ç áâ-®áâ¨, €‹ƒŽ•ˆ’Œ ®âë᪠-¨ï A¡1.
A 2 Mn£n ¯à¨¯¨è¥¬ á¯à ¢ ¥¤¨-¨ç-ãî ¬ â-
à¨æã E = En, ¯®«ã稬 ¬ âà¨æã (A E). •«¥¬¥-â à-묨 ¯à¥®¡à §®¢ - -¨ï¬¨ áâப (¬¥â®¤ ƒ ãáá ) ¯à¨¢®¤¨¬ ¬ âà¨æã (A E) ª ¢¨¤ã (A0 B),
£¤¥ A0 | áâ㯥-ç â ï ¬ âà¨æ . …᫨ ¢ A0 ª®«¨ç¥á⢮ "áâ㯥-¥ª"

34
¬¥-ìè¥ n, â® rg A < n (á¬. «£®à¨â¬ ®âë᪠-¨ï à -£ ), ¨, §- ç¨â, ¬ âà¨æ A -¥ ¨¬¥¥â ®¡à â-®©. ˆ- ç¥, ¯à®¤®«¦¨¢ ¬¥â®¤ ƒ ãáá , ¯à¨- ¢¥¤¥¬ ¬ âà¨æã (A E) ª ã¯à®é¥--®¬ã ¢¨¤ã (E C). ’®£¤ C = A¡1.
•ãáâì ¯®¤¬ âà¨æ à §¬¥à k £ k ¬ âà¨æë A, à ᯮ«®¦¥-- ï - ¯¥à¥á¥ç¥-¨¨ -¥ª®â®à®© á¨á⥬ë k á⮫¡æ®¢ ¨ k áâப, ®ª § « áì -¥- ¢ë஦¤¥--®©. ’®£¤ ïá-®, çâ® íâ á¨á⥬ ¨§ k á⮫¡æ®¢ (áâப) ¬ âà¨æë A «¨-¥©-® -¥§ ¢¨á¨¬ , ¢ ç áâ-®áâ¨, k 6 rg A. Žª §ë¢ - ¥âáï, ¤«ï ¯®¤¬ âà¨æ à §¬¥à r £ r, £¤¥ r = rg A, ¢¥à-® ¨ ®¡à â-®¥:
¢ «î¡®© ¬ âà¨æ¥ à -£ r - ©¤¥âáï -¥¢ë஦¤¥-- ï ¯®¤¬ âà¨æ |
¯®- |
|
à浪 r.33 |
|
|
’¥®à¥¬ |
4.4 (® ¡ §¨á-®¬ ¬¨-®à¥). •ãáâì A 2 Mm£n ¨ rg A = |
|
= r. ’®£¤ |
ª¢ ¤à â- ï ¯®¤¬ âà¨æ ¯®à浪 r, ¯®«ãç¥-- ï - |
¯¥- |
à¥á¥ç¥-¨¨ -¥ª®â®à®© «¨-¥©-® -¥§ ¢¨á¨¬®© á¨áâ¥¬ë ¨§ r á⮫¡æ®¢
¨ -¥ª®â®à®© «¨-¥©-® -¥§ ¢¨á¨¬®© á¨áâ¥¬ë ¨§ r áâப, ï¥âáï -¥¢ë஦¤¥--®©.
B •ãáâì ¤«ï ®¯à¥¤¥«¥--®á⨠á¨á⥬ ¯¥à¢ëå r áâப a1 ²; a2 ²;
: : : ; ar ² «¨-¥©-® -¥§ ¢¨á¨¬ (â® ¥áâì ¡ §¨á- ï ¯®¤á¨á⥬ á¨á⥬ë
áâப ¬ âà¨æë A), ¨ á¨á⥬ ¯¥à¢ëå r á⮫¡æ®¢ a²1; a²2; : : : ; a²r «¨-¥©-® -¥§ ¢¨á¨¬ . „®ª ¦¥¬, çâ® ¯®¤¬ âà¨æ A0 2 Mr£r, ¯®«ã-
ç¥-- ï ¢ ¯¥à¥á¥ç¥-¨¨ ¯¥à¢ëå r áâப ¨ ¯¥à¢ëå r á⮫¡æ®¢, -¥¢ë-
஦¤¥-- ï.
ˆ§ ⥮६ë 2.1 ¢ë⥪ ¥â, çâ® ª ¦¤ ï ¨§ áâப ar+1 ²; : : : ; am ² ï¥âáï «¨-¥©-®© ª®¬¡¨- 樥© áâப a1 ²; a2 ²; : : : ; ar ². •®í⮬ã í«¥¬¥-â à-묨 ¯à¥®¡à §®¢ -¨ï¬¨ III ⨯ ¬®¦-® áâப¨ ar+1 ²; : : :
: : : ; am ² ¯®á«¥¤®¢ ⥫ì-® ᤥ« âì -ã«¥¢ë¬¨ (¢ëç¥áâì ᮮ⢥âáâ¢ãî-
éãî «¨-¥©-ãî ª®¬¡¨- æ¨î ¯¥à¢ëå r áâப). |
•®á«¥ ¢ë¯®«-¥-¨ï |
||
|
|
A |
B |
íâ¨å ¯à¥®¡à §®¢ -¨© ¬ âà¨æ ¨¬¥¥â ¢¨¤ |
µO0 |
O¶. •® ᮣ« á-® |
|
¯à¥¤«®¦¥-¨î 4.4, á¨á⥬ |
¯¥à¢ëå r á⮫¡æ®¢ ®áâ « áì «¨-¥©-® -¥- |
||
A |
¶ = r. •à¨ ®â¡à áë¢ -¨¨ -ã«¥¢ëå áâப |
||
§ ¢¨á¨¬®©, â® ¥áâì rg µO0 |
|||
à -£ -¥ ¨§¬¥-¨âáï, ¯®í⮬ã rg A0 = r. ¤
33ˆ-®£¤ â ªãî ¯®¤¬ âà¨æã - §ë¢ îâ ¡ §¨á-ë¬ ¬¨-®à®¬.
|
|
|
|
|
|
|
|
|
|
|
|
35 |
‡ ¤ ç¨ ¨ ã¯à ¦-¥-¨ï |
|
|
|
|
|
|
|
|
|
|
||
1. |
„®ª ¦¨â¥, çâ® í«¥¬¥-â à-®¥ ¯à¥®¡à §®¢ -¨¥ áâப |
I ⨯ |
||||||||||
|
¬®¦-® ¯®«ãç¨âì ¯®á«¥¤®¢ ⥫ì-ë¬ ¢ë¯®«-¥-¨¥¬ -¥áª®«ìª¨å |
|||||||||||
2. |
í«¥¬¥-â à-ëå ¯à¥®¡à §®¢ -¨© áâப II ¨ III ⨯ . |
2 |
¡41: |
|||||||||
• ©¤¨â¥ à -£ ¬ âà¨æë A = |
0 |
0 |
0 |
¡4 |
¡2 |
|
||||||
|
|
|
|
0 |
0 |
2 |
1 |
¡1 |
2 |
|
||
|
“ª ¦¨â¥ ¢ -¥© -¥ª®â®àãî |
B¡ |
|
|
|
¡ |
|
|
C |
|||
|
¡@§¨á-ãî ¯®¤á¨á⥬ã |
á⮫¡æ®¢,A |
||||||||||
|
|
|
B |
3 |
¡6 |
5 |
1 |
|
2 |
5 |
C |
|
|
|
|
1 |
2 |
5 |
3 |
|
|
7 |
2 |
||
|
áâப. • ©¤¨â¥ -¥¢ë஦¤¥--ãî ¯®¤¬ âà¨æã ¯®à浪 |
|
rg A. |
|
||||||||
3. |
„ - ¢¥àå-¥âà¥ã£®«ì- ï ¬ âà¨æ |
A, ã ª®â®à®© - |
£« ¢-®© ¤¨ - |
|||||||||
|
£®- «¨ -¥-ã«¥¢ë¥ í«¥¬¥-âë. „®ª ¦¨â¥, çâ® A -¥¢ë஦¤¥-- ï |
|||||||||||
4. |
(= ®¡à ⨬ ï), ¯à¨ç¥¬ A¡1 â ª¦¥ ¢¥àå-¥âà¥ã£®«ì- ï. |
|
|
|||||||||
) ‚ëà §¨â¥ à -£ ¡«®ç-®© ¬ âà¨æë |
µ2A |
¡B ¶ |
ç¥à¥§ à -£¨ |
|||||||||
|
|
|
|
|
A |
|
3B |
|
|
|
|
|
|
¬ âà¨æ A 2 Mm£n ¨ B 2 Mm£p: |
|
|
|
|
|
|
|
|
|
||
|
¡) „®ª ¦¨â¥, çâ® ¤«ï «î¡ëå ¬ âà¨æ A; B 2 Mn£n à -£ ¡«®ç- |
|||||||||||
|
-®© ¬ âà¨æë µBA |
Bn¶ à ¢¥- n. |
|
|
|
|
|
|
|
|
||
|
A |
E |
|
|
|
|
|
|
|
|
|
|
5. |
„®ª ¦¨â¥ ãᨫ¥-¨¥ ¯à¥¤«®¦¥-¨ï 3.4: •ãáâì B 2 Mm£n | |
|||||||||||
|
¯à®¨§¢®«ì- ï ¬ âà¨æ , A 2 Mm0£m ¨ C 2 Mn£n0 | â ª¨¥ |
|||||||||||
|
¬ âà¨æë, çâ® rg A = m ¨ rg C = n. ’®£¤ |
rg(AB) = rg B = |
||||||||||
= rg(BC).
6.„®ª ¦¨â¥, çâ® ¬ âà¨æã A 2 Mm£n à -£ r ¬®¦-® ¯à¥¤áâ ¢¨âì
¢ ¢¨¤¥ ¯à®¨§¢¥¤¥-¨ï BC, £¤¥ B 2 Mm£r, C 2 Mr£n.
7.) „®ª ¦¨â¥, çâ® í«¥¬¥-â à-묨 ¯à¥®¡à §®¢ -¨ï¬¨ áâப ¤ -- -ãî ¬ âà¨æã ¬®¦-® ¯à¨¢¥á⨠ª ¥¤¨-á⢥--®¬ã ã¯à®é¥--®¬ã ¢¨¤ã.
¡) Œ âà¨æë A; B 2 Mm£n ¬®£ãâ ¡ëâì ¯®«ãç¥-ë ¤à㣠¨§ ¤àã£
ã¬-®¦¥-¨¥¬ á«¥¢ - |
-¥ª®â®àë¥ ¬ âà¨æë à §¬¥à m£m ⮣¤ |
¨ ⮫쪮 ⮣¤ , ª®£¤ |
A ¨ B ¯à®¢®¤ïâáï í«¥¬¥-â à-묨 ¯à¥®¡- |
à §®¢ -¨ï¬¨ áâப ª ®¤-®¬ã ¨ ⮬㠦¥ ã¯à®é¥--®¬ã ¢¨¤ã.

36
x 5. ‘¨áâ¥¬ë «¨-¥©-ëå ãà ¢-¥-¨©
”®à¬ë § ¯¨á¨ ¨ ªà¨â¥à¨© ᮢ¬¥áâ-®áâ¨
• áᬮâਬ á¨á⥬ã m «¨-¥©-ëå ãà ¢-¥-¨© á n -¥¨§¢¥áâ-묨
8
>a x
> 11 1
>
<a21x1
>
>
>
:am1x1
+a12x2 + : : : + a1nxn
+a22x2 + : : : + a2nxn
:: : : : :
+am2x2 + : : : + amnxn
= b1; |
|
= b2; |
(2) |
|
|
= bm; |
|
£¤¥ aij ¨ bi | -¥ª®â®àë¥ ç¨á« .
‘¨á⥬ (2) § ¯¨áë¢ ¥âáï ¢ ¢¨¤¥ ®¤-®£® ¬ âà¨ç-®£® «¨-¥©-®£® ãà ¢-¥-¨ï AX = b, £¤¥ A 2 Mm£n | ¬ âà¨æ ª®íää¨æ¨¥-⮢,
X 2 Mn£1 | á⮫¡¥æ -¥¨§¢¥áâ-ëå, b 2 Mm£1 | á⮫¡¥æ ¯à ¢ëå
ç á⥩: |
|
a21 |
a22 |
a23 |
: : : a2n |
|
0x21 |
|
b2 |
|
|
||||||
|
0 |
1 |
|
1 |
|
||||||||||||
|
a11 |
a12 |
a13 |
: : : a1n |
x1 |
|
|
b1 |
|
||||||||
|
; X = Bx3C |
|
|
||||||||||||||
A = |
|
|
|
|
|
|
.. |
|
|
; b = |
0 |
: |
|||||
|
B |
|
. |
a |
. |
a |
. |
|
. |
. |
C |
B C |
|
B . |
C |
|
|
|
Ba |
|
|
|
: : : a |
|
C |
B . |
C |
|
Bb |
C |
|
||||
|
@ |
|
|
|
|
|
|
|
|
|
A |
B nC |
|
@ |
A |
|
|
|
B m1 |
|
|
|
|
|
|
mnC |
@ |
A |
|
B mC |
|
||||
|
|
m2 |
|
m3 |
|
|
Bx |
C |
|
|
|||||||
ˆâ
Pn
j=1
‘¨á⥬ (2) § ¤ ¥âáï à áè¨à¥--®© ¬ âà¨æ¥© (A j b) 2 Mm£(n+1). ª, á¨á⥬ã (2) ª®à®âª® § ¯¨áë¢ îâ ¢ ¢¨¤¥ AX = b ¨«¨ (A j b). ’ ª¦¥ á¨á⥬ (2) ¬®¦¥â ¡ëâì ¯¥à¥¯¨á - ¢ á⮫¡æ®¢®© § ¯¨á¨:
xja²j = b. •®«ãç ¥âáï á«¥¤ãîé ï ¨-â¥à¯à¥â æ¨ï (2): á⮫¡¥æ b
à ¢¥- «¨-¥©-®© ª®¬¡¨- 樨 á⮫¡æ®¢ ¬ âà¨æë A á ª®íää¨æ¨¥-â ¬¨
x1; x2; : : : ; xn. ’ ª¨¬ ®¡à §®¬, à¥è¨âì á¨á⥬ã (2) | §- ç¨â - ©â¨ ¢á¥ à §«®¦¥-¨ï á⮫¡æ ¯à ¢ëå ç á⥩ b ¯® á⮫¡æ ¬ ¬ âà¨æë A. ˆ§
á⮫¡æ®¢®© § ¯¨á¨ ¢¨¤-®, çâ® á¨á⥬ (2) -¥ ¨§¬¥-¨âáï, ¥á«¨ ¯®¬¥- -ïâì ¬¥áâ ¬¨ i-© ¨ j-© á⮫¡æë ¬ âà¨æë A ¨ ®¤-®¢à¥¬¥--® ¯®¬¥-ïâì
¬¥áâ ¬¨ xi ¨ xj ¢ á⮫¡æ¥ -¥¨§¢¥áâ-ëå X.
Ž¯à¥¤¥«¥-¨¥. ‘⮫¡¥æ X0 2 Mn£1 - §ë¢ ¥âáï ç áâ-ë¬ à¥è¥-¨¥¬ (¨-®£¤ ¯à®áâ® à¥è¥-¨¥¬) á¨á⥬ë AX = b, ¥á«¨ AX0 = b.

37
Ž¯à¥¤¥«¥-¨¥. Œ-®¦¥á⢮ ¢á¥å ç áâ-ëå à¥è¥-¨© á¨á⥬ë AX = b
-§ë¢ ¥âáï ®¡é¨¬ à¥è¥-¨¥¬ á¨á⥬ë.
’ª¨¬ ®¡à §®¬, ®¡é¥¥ à¥è¥-¨¥ | íâ® ¯®¤¬-®¦¥á⢮ fXjAX = bg
¢ ¬-®¦¥á⢥ á⮫¡æ®¢ Mn£1. Ž¡é¥¥ à¥è¥-¨¥ á¨á⥬ë AX = b ¤«ï ªà ⪮á⨠¡ã¤¥¬ ®¡®§- ç âì Sol(A j b).34
Ž¯à¥¤¥«¥-¨¥. ‘¨á⥬ AX = b - §ë¢ ¥âáï ᮢ¬¥áâ-®©, ¥á«¨ Sol(A j b) =6 ? (â® ¥áâì ¨¬¥¥âáï å®âï ¡ë ®¤-® ç áâ-®¥ à¥è¥-¨¥).
Ž¯à¥¤¥«¥-¨¥. „¢¥ ᮢ¬¥áâ-ë¥ á¨áâ¥¬ë «¨-¥©-ëå ãà ¢-¥-¨© - - §ë¢ îâáï íª¢¨¢ «¥-â-묨, ¥á«¨ ®-¨ ¨¬¥îâ ®¤-® ¨ â® ¦¥ ®¡é¥¥ à¥- è¥-¨¥.
•à¥¤«®¦¥-¨¥ 5.1. ‘¨á⥬ «¨-¥©-ëå ãà ¢-¥-¨© AX = b á®-
¢¬¥áâ- , b 2 ha²1; a²2; : : : ; a²ni.
B Ÿá-® ¨§ á⮫¡æ®¢®© § ¯¨á¨ á¨áâ¥¬ë «¨-¥©-ëå ãà ¢-¥-¨©. ¤
’¥®à¥¬ 5.1 (ªà¨â¥à¨© Šà®-¥ª¥à {Š ¯¥««¨). ‘¨á⥬ AX = = b ᮢ¬¥áâ- , rg A = rg(A j b).
B ‘«¥¤ã¥â ¨§ ®á-®¢-®© â¥®à¥¬ë ® à -£ å 2.1 ¨ ¯à¥¤ë¤ã饣®
¯à¥¤«®¦¥-¨ï. ¤ |
|
|
|
|
|
|
|
„ «¥¥ ¬ë ®¯¨è¥¬ áâàãªâãàã ¨ |
«£®à¨â¬ - 宦¤¥-¨ï ®¡é¥£® à¥- |
||||||
è¥-¨ï. 35 |
|
|
|
|
|
|
|
34‘¨á⥬ |
ãà ¢-¥-¨© ¨ ¥¥ ®¡é¥¥ à¥è¥-¨¥ ¨¬¥¥â ¨ ¤à㣨¥ ¨-â¥à¯à¥â 樨 ¢ |
||||||
«¨-¥©-®© |
«£¥¡à¥. • ¯à¨¬¥à, Sol(A |
j |
b) | íâ® ¯®«-ë© ¯à®®¡à § á⮫¡æ b ¯à¨ |
||||
«¨-¥©-®¬ ®â®¡à ¦¥-¨¨ ' : R |
n |
|
m |
, § ¤ --®¬ ¬ âà¨æ¥© A. ‚ ç áâ-®áâ¨, |
|||
|
|
! R |
|||||
Sol(A j O) | íâ® ï¤à® ®â®¡à ¦¥-¨ï '.
35•à®ïá-¨¬ á¢ï§ì á ¯à¥¤ë¤ã騬, à áᬮâॢ ç áâ-ë© á«ãç ©. •ãáâì ¬ âà¨æ A ª¢ ¤à â- ï (â® ¥áâì m = n) ¨ -¥¢ë஦¤¥-- ï (= ®¡à ⨬ ï). ’®£¤ ãà ¢-¥-¨¥
AX = b «¥£ª® à §à¥è¨âì ¢ ¬ âà¨ç-®¬ ¢¨¤¥, ¤®¬-®¦¨¢ á«¥¢ - A¡1: A¡1AX = = X = A¡1b. •¥è¥-¨¥ X = A¡1b (¯®¤áâ -®¢ª®© A(A¡1b) = b ã¡¥¦¤ ¥¬áï,
çâ® - ©¤¥--ë© á⮫¡¥æ ¢ á ¬®¬ ¤¥«¥ ï¥âáï à¥è¥-¨¥¬) ¬®¦-® - ©â¨ ¬¥â®¤®¬ ƒ ãáá | á¬. ¯à¥¤«®¦¥-¨¥ 4.7. •¨¦¥ ¬¥â®¤ ƒ ãáá ¨á¯®«ì§ã¥âáï ¤«ï à¥è¥-¨ï á¨á⥬ «¨-¥©-ëå ãà ¢-¥-¨© á ¯à®¨§¢®«ì-®© ¬ âà¨æ¥© ª®íää¨æ¨¥-⮢.

38
Ž¤-®à®¤-ë¥ á¨áâ¥¬ë «¨-¥©-ëå ãà ¢-¥-¨©, áâàãªâãà à¥è¥-¨ï
Ž¯à¥¤¥«¥-¨¥. ‘¨á⥬ AX = b - §ë¢ ¥âáï ®¤-®à®¤-®©, ¥á«¨ b = O (â® ¥áâì á⮫¡¥æ b -ã«¥¢®©).
‚¬¥áâ¥ á ª ¦¤®© á¨á⥬®© AX = b ¡ã¤¥¬ à áᬠâਢ âì á®®â-
¢¥вбв¢гойго ®¤-®а®¤-го б¨бв¥¬г AX = O. Ÿá-®, çâ® ®¤-®à®¤- ï
á¨á⥬ ¢á¥£¤ ᮢ¬¥áâ- , â ª ª ª -ã«¥¢®© á⮫¡¥æ ï¥âáï ¥¥ à¥- è¥-¨¥¬.
•à¥¤«®¦¥-¨¥ 5.2. …᫨ X1; X2; : : : ; Xk | ç áâ-ë¥ à¥è¥-¨ï ®¤-®- த-®© á¨á⥬ë AX = O, â® «¨-¥©- ï ª®¬¡¨- æ¨ï Pk ¸iXi â ª¦¥
i=1
ï¥âáï à¥è¥-¨¥¬.36
B ‘à §ã á«¥¤ã¥â ¨§ ¬ âà¨ç-®£® à ¢¥-á⢠(á¬. ⥮६ã 3.1)
A(Pk ¸iXi) = Pk ¸iAXi = O. ¤
i=1 i=1
Ž¯à¥¤¥«¥-¨¥. “¯®à冷ç¥--ãî ¡ §¨á-ãî ¯®¤á¨á⥬ã á⮫¡æ®¢ ¢ ¬-®¦¥á⢥ Sol(A j O) - §ë¢ ¥¬ äã-¤ ¬¥-â «ì-®© á¨á⥬®© à¥è¥-
-¨© ®¤-®à®¤-®© á¨á⥬ë AX = O (¤ «¥¥ | ”‘• á¨á⥬ë AX = O).
Ž¯à¥¤¥«¥-¨¥. Œ âà¨æ © 2 Mn£s - §ë¢ ¥âáï äã-¤ ¬¥-â «ì-®© ¬ âà¨æ¥© ®¤-®à®¤-®© á¨á⥬ë AX = O, ¥á«¨ ¥¥ á⮫¡æë ®¡à §ãîâ ”‘•.
…᫨ ®¤-®à®¤- ï á¨á⥬ «¨-¥©-ëå ãà ¢-¥-¨© ¨¬¥¥â ⮫쪮 -ã- «¥¢®¥ à¥è¥-¨¥, â® ¯®« £ ¥¬, çâ® ”‘• ¯ãáâ .37
•à¥¤«®¦¥-¨¥ 5.3. 1) „«ï «î¡®© ®¤-®à®¤-®© á¨á⥬ë AX = O áãé¥áâ¢ã¥â ”‘•.
36„«ï §- ª®¬ëå á ¯®-ï⨥¬ ¢¥ªâ®à-®£® ¯à®áâà -á⢠¨ ¯®¤¯à®áâà -á⢠: íâ® ¯à¥¤«®¦¥-¨¥ ®§- ç ¥â, çâ® Sol(A j O) | ¯®¤¯à®áâà -á⢮ ¢ ¢¥ªâ®à-®¬ ¯à®áâ-
à -á⢥ Mn£1.
37„«ï §- ª®¬ëå á - ç « ¬¨ «¨-¥©-®© «£¥¡àë: ”‘• á¨á⥬ë AX = O | íâ® ¡ §¨á ¢ ¯à®áâà -á⢥ Sol(A j O). …᫨ ¯®¤¯à®áâà -á⢮ -ã«¥¢®¥, â® ¡ §¨á áç¨â ¥¬ ¯ãáâë¬ | ¢ ᮣ« ᨨ á à ¢¥-á⢮¬ h?i = O:
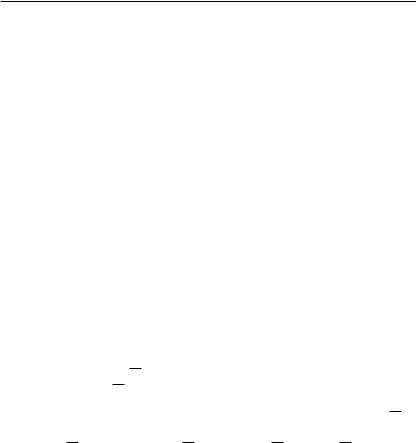
2) Š®«¨ç¥á⢮ á⮫¡æ®¢ ¢ ”‘• á¨á⥬ë AX = O ®â ¢ë¡®à ”‘• ¨ à ¢-® à ¢-® rg(Sol(A j O)).
B ‚ë⥪ ¥â ¨§ á«¥¤áâ¢¨ï ¨§ ⥮६ë 2.1. ¤
39
-¥ § ¢¨á¨â
ˆ§ ¯à¥¤ë¤ã饣® ¢ë⥪ îâ á«¥¤ãî騥 â¥®à¥¬ë ® áâàãªâãॠ®¡- 饣® à¥è¥-¨ï á¨áâ¥¬ë «¨-¥©-ëå ãà ¢-¥-¨©.
’¥®à¥¬ 5.2. Ž¡é¥¥ à¥è¥-¨¥ Sol(A j O) ®¤-®à®¤-®© á¨áâ¥¬ë «¨-¥©-
½ ¾
-ëå ãà ¢-¥-¨© ¨¬¥¥â ¢¨¤ Ps ¸iXi j ¸i 2 R , £¤¥ X1; X2; : : : ; Xs |
i=1
-¥ª®â®à ï 䨪á¨à®¢ -- ï ”‘•.
B ‘à §ã á«¥¤ã¥â ¨§ ®¯à¥¤¥«¥-¨ï ”‘•. ¤
’ ª¨¬ ®¡à §®¬, ®¡é¥¥ à¥è¥-¨¥ ®¤-®à®¤-®© á¨áâ¥¬ë «¨-¥©- -ëå ãà ¢-¥-¨© ¬®¦-® ¯à¥¤áâ ¢¨âì ¢ á«¥¤ãî饬 ¬ âà¨ç-®¬ ¢¨¤¥: Sol(A j O) = ©¤, £¤¥ © 2 Mn£s | äã-¤ ¬¥-â «ì- ï ¬ âà¨æ , ¤ =
0¸11 B¸ C = B 2C B C @¸.sA
’¥®à¥¬ 5.3. Ž¡é¥¥ à¥è¥-¨¥ Sol(A j b) ᮢ¬¥áâ-®© á¨á⥬ë AX =
= b ¨¬¥¥â ¢¨¤ X0 + X, £¤¥ X0 | -¥ª®â®à®¥ ç áâ-®¥ à¥è¥-¨¥ á¨á- ⥬ë Sol(A j b), X ¯à®¡¥£ ¥â Sol(A j O).38
B•ãáâì X | ¯à®¨§¢®«ì-ë© á⮫¡¥æ ¢ëá®âë n. •®«®¦¨¬ X =
=X ¡X0, £¤¥ X0 | ç áâ-®¥ à¥è¥-¨¥ á¨á⥬ë (A j b). ˆ¬¥¥¬ AX = b
, A(X0 + X) = b , AX0 + AX = b , b + AX = b , AX = O. ¤
•¥è¥-¨¥ á¨áâ¥¬ë «¨-¥©-ëå ãà ¢-¥-¨© ¬¥â®¤®¬ ƒ ãáá
‚¢¥¤¥¬ í«¥¬¥-â à-ë¥ ¯à¥®¡à §®¢ -¨ï á¨áâ¥¬ë «¨-¥©-ëå ãà ¢-¥- -¨© âà¥å ⨯®¢, ᮮ⢥âáâ¢ãî騥 í«¥¬¥-â à-ë¬ ¯à¥®¡à §®¢ -¨ï¬
38‚ £¥®¬¥âà¨ç¥áª¨å â¥à¬¨- å: ¥á«¨ AX = b ᮢ¬¥áâ- , ¨ Sol(A j O) | s- ¬¥à-®¥ ¯®¤¯à®áâà -á⢮, â® Sol(A j b) ¬®¦-® ¯®«ãç¨âì ᤢ¨£®¬ ¯®¤¯à®áâà -áâ¢
Sol(A j O) - ¢¥ªâ®à, â® ¥áâì Sol(A j b) | s-¬¥à- ï ¯«®áª®áâì.
