Документ Microsoft Office Word
.docx4
Материальная
точка –
геометрическая
точка, которой поставлено в соответствие
положительное число
 - масса.
- масса.
Твердое тело – такая совокупность материальных точек, что расстояние между любыми двумя неизменно.
Рассмотрим
декартову систему координат
 ,
в которой расположено твердое тело (см.
рис. 11).
,
в которой расположено твердое тело (см.
рис. 11).

Рисунок 1
С
твердым телом,
в свою очередь, жестко
связана другая
система
координат
 ,
с началом в точке
,
с началом в точке
 твердого тела и движущаяся относительно
неподвижного пространства.
твердого тела и движущаяся относительно
неподвижного пространства.
Нас
интересует скорость и ускорение точки
 ,
принадлежащей твердому телу.
,
принадлежащей твердому телу.
Радиус-вектор
точки
 определяется выражением:
определяется выражением:
 .
.
Следует
отметить, что
 постоянен по модулю:
постоянен по модулю:
 .
.
В
греческой системе координат
 :
:
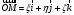 ,
,
причем
 - постоянные, а
- постоянные, а
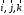 - движутся относительно
- движутся относительно
 .
.
Введем
вектор
 таким образом, что
таким образом, что
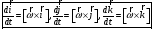 .
.
Здесь
и далее
 означает векторное произведение.
означает векторное произведение.
Введенный
таким образом вектор
 называют угловой
скоростью твердого тела.
называют угловой
скоростью твердого тела.
Тогда
скорость точки
 равна (эту формулу называют законом
распределения скоростей в твердом
теле):
равна (эту формулу называют законом
распределения скоростей в твердом
теле):
 ,
,
поскольку

Аналогично
можно получить ускорение точки
 (закон
распределения ускорений в твердом
теле):
(закон
распределения ускорений в твердом
теле):

где
 - угловое
ускорение.
- угловое
ускорение.
В
случае, когда
точка
 неподвижна,
неподвижна,

и для определенности вводят термины:
 - вращательное
ускорение,
- вращательное
ускорение,
 - осестремительное
ускорение.
- осестремительное
ускорение.
Осестремительное
ускорение всегда направлено к мгновенной
оси вращения,
т.е. к оси проходящей через вектор
 (геометрическое место точек с нулевыми
мгновенными скоростями).
(геометрическое место точек с нулевыми
мгновенными скоростями).
Если
рассматривается движение с неподвижной
осью, то точку
 целесообразно брать на оси (см. рис. 12).
целесообразно брать на оси (см. рис. 12).
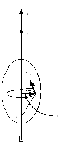
Рисунок 2
Тогда
 направлено по
касательной к окружности радиуса
направлено по
касательной к окружности радиуса
 .
.

Но
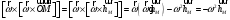 ,
,
где
 - вектор, задающий расстояние от оси до
точки
- вектор, задающий расстояние от оси до
точки
 ,
,
 ,
поскольку
,
поскольку
 .
.
В
итоге получаем
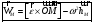 .
.
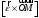 - совпадает по
направлению с
- совпадает по
направлению с
 ,
,
 - направлено в
противоположную
- направлено в
противоположную
 сторону.
сторону.
При раскрытии векторного произведения использовалось правило:
 .
.
Когда
мгновенная ось неподвижна ( ),
тогда вращательное ускорение
),
тогда вращательное ускорение
 совпадает с касательным
совпадает с касательным
 и осестремительное ускорение
и осестремительное ускорение
 совпадает с нормальным
совпадает с нормальным
 .
В общем случае (
.
В общем случае ( ),
данное соотношение не выполняется, и
кроме того,
),
данное соотношение не выполняется, и
кроме того,
 и
и
 не ортогональны.
не ортогональны.
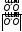
На
рис. 13 указаны направления ускорений
для случая
 .
.

Рисунок 3
 - проекция точки
- проекция точки
 на ось
на ось
 ,
,
 - вектор от оси
- вектор от оси
 к точке
к точке
 ,
,
 направлено по
касательной к окружности радиуса
направлено по
касательной к окружности радиуса
 ,
,
 направлено к
мгновенной оси
направлено к
мгновенной оси
 .
.
Запишем
 ,
где
,
где
 - единичный орт вдоль
- единичный орт вдоль
 .
.
Тогда
 .
.
Введем
вектор
 таким образом, что
таким образом, что
 .
.
Т.к.
 задает направление мгновенной оси, то
задает направление мгновенной оси, то
 является
угловой скоростью поворота вектора
угловой скорости
является
угловой скоростью поворота вектора
угловой скорости
 .
.
В итоге,

Первая
компонента
 соответствует изменению угловой скорости
по модулю,
вторая компонента
соответствует изменению угловой скорости
по модулю,
вторая компонента
 соответствует
изменению угловой скорости по направлению.
соответствует
изменению угловой скорости по направлению.
5
Рассмотрим подробнее плоскопараллельное движение.
Это движение твердого тела, при котором движения всех его точек лежат в плоскостях параллельных некоторой плоскости.
Формулу
 можно преобразовать в более простую.
можно преобразовать в более простую.
Т.к.
при плоскопараллельном движении
 ,
,
 ,
то
,
то

Знание скоростей любых двух точек при плоскопараллельном движении позволяет найти мгновенный центр скоростей или, другими словами, мгновенную ось вращения (см. рис. 14).

Рисунок 4
Мгновенная
ось восстанавливается как пересечение
перпендикуляров к
 и
и
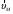 ,
а
,
а
 .
Распределение скоростей такое, как если
бы было чистое вращение:
.
Распределение скоростей такое, как если
бы было чистое вращение:
 .
.
Пример. Качение без проскальзывания.
В задачах данное выражение значит, что в точке касания твердого тела с поверхностью скорость тела равна скорости поверхности.
Если поверхность неподвижна, то скорость точки касания равна нулю (см. рис. 15).

Рисунок 5
Есть еще одно важное замечание, которое является свойством твердого тела (неразрывность и несжимаемость):
Проекции скоростей любых двух точек твердого тела на прямую соединяющую их равны (см. рис. 16), т.е.


Рисунок 6
Исходя из этого оценим возможные варианты распределения скоростей при плоскопараллельном движении (рис. 17).

Рисунок 7
6
Основные характеристики системы векторов – главный вектор и главный момент.

Рисунок 8
 -
главный вектор.
-
главный вектор.
Момент вектора относительно полюса:


Рисунок 9
 - главный
момент.
- главный
момент.
Главный момент является связанным вектором

Есть
компоненты, которые не меняются при
переходе к
 .
.
Домножим
 на
на
 :
:

Т.е. проекции главных моментов относительно двух полюсов на линию, соединяющую полюса, равны.
Домножим
 на
на
 :
:

Т.е. проекция главного момента на направление главного вектора не зависит от выбора полюса.
Итого, имеется два инварианта системы векторов относительно выбора полюса:
-
Главный вектор
-
Проекция главного момента на главный вектор.
Рассмотрим задачу приведения системы скользящих векторов к простому виду. Решаем данную задачу с следующей целью: какими бы сложными ни были движения по сути их можно представить одним простым видом движения.
Вводится понятие эквивалентности систем скользящих векторов. Мы должны получить систему, эквивалентную исходной.
Две системы скользящих векторов называются эквивалентными, если одна из другой получается с помощью элементарных операций: добавление элементарного векторного нуля, и сложение и разложение векторов по правилу параллелограмма.

Рисунок 10
Критерий эквивалентности – две системы скользящих векторов эквивалентны в том и только в том случае, если равны их главные векторы и главные моменты относительно произвольно выбранного полюса.
Лемма. Произвольная система векторов может быть приведена к двум векторам, один из которых приложен к произвольной точке.
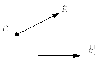
Рисунок 11
Приведение системы скользящих векторов к выбранному полюсу:

Рисунок 12
Просто перенести скользящий вектор без добавления пары (момента) мы не можем.
Рассмотрим все возможные случаи приведенных систем скользящих векторов:
1.
 (винт)
(винт)
Проекция
 неизменна, т.к. является вторым инвариантом,
т.е. проекцией главного момента на
главный вектор.
неизменна, т.к. является вторым инвариантом,
т.е. проекцией главного момента на
главный вектор.


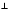 плоскости
плоскости

Найдется
такая точка
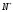 ,
что
,
что


Рисунок 13
Предположим,
есть еще такая точка
 :
:

Тогда
 должна лежать на параллели
должна лежать на параллели
 и проходить через
и проходить через
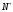 .
На линии, проходящей через
.
На линии, проходящей через
 и
и
 ,
главный момент будет иметь минимальное
значение. При этом главный момент равен
,
главный момент будет иметь минимальное
значение. При этом главный момент равен
 ,
и называется моментом
винта.
,
и называется моментом
винта.
Другими словами, приводя систему векторов к виду, при котором главный вектор и главный момент параллельны, мы приводим систему векторов к винту.

Рисунок 14
Также говорят, приводим систему скользящих векторов к простейшему виду.

Рисунок 15
Найдем уравнение оси минимальных моментов из условия параллельности главного момента и главного вектора.


- векторная запись уравнения оси минимальных моментов.

Тогда,
 ,
,
 ,
,

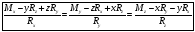
Координатная запись уравнения оси минимальных моментов.
2.
 (равнодействующая)
(равнодействующая)
Систему
характеризует только один инвариант,
 - равнодействующая, к которой система
сводится.
- равнодействующая, к которой система
сводится.
К
данному случаю относится также вариант


3.
 (равнодействующая пара)
(равнодействующая пара)
Чистое поворачивающее усилие:

4.
 (равновесие)
(равновесие)
Векторный нуль:

Пример.
|
Случай |
Теория скользящих векторов |
Кинематика |
|
|
Винт |
Кинематический винт |
|
|
Равнодействующая |
Вращение |
|
|
Равнодействующая пара |
Поступательное движение |
|
|
Равновесие |
Покой |

Рисунок 16

Т.е. момент угловой скорости является скоростью.
В
кинематике
 соответствует
соответствует
 ,
а
,
а
 соответствует
соответствует
 .
.
Пример.

Рисунок 17
Тело
совершает винтовой движение, а другое
тело вращается относительно оси
 .
.
Найти простейший вид относительного движения первого тела относительно второго.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,



Если
 - чистое вращение.
- чистое вращение.
Если
 - винтовое движение.
- винтовое движение.
Уравнение оси минимальных моментов:

Отсюда,
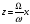
 ,
,
15
Величина и направление – свободный вектор.
Величина и линия действия – скользящий вектор.
Величина и точка приложения – приложенный (связанный) вектор.
Например, вектор угловой скорости относится к скользящим.
Основные характеристики системы векторов – главный вектор и главный момент.

Рисунок 18
 -
главный вектор.
-
главный вектор.
Момент вектора относительно полюса:


Рисунок 19
 - главный
момент.
- главный
момент.
Главный момент является связанным вектором

Есть
компоненты, которые не меняются при
переходе к
 .
.
Домножим
 на
на
 :
:

Т.е. проекции главных моментов относительно двух полюсов на линию, соединяющую полюса, равны.
Домножим
 на
на
 :
:

Т.е. проекция главного момента на направление главного вектора не зависит от выбора полюса.
Итого, имеется два инварианта системы векторов относительно выбора полюса:
-
Главный вектор
-
Проекция главного момента на главный вектор.
Рассмотрим задачу приведения системы скользящих векторов к простому виду. Решаем данную задачу с следующей целью: какими бы сложными ни были движения по сути их можно представить одним простым видом движения.
Вводится понятие эквивалентности систем скользящих векторов. Мы должны получить систему, эквивалентную исходной.
Две системы скользящих векторов называются эквивалентными, если одна из другой получается с помощью элементарных операций: добавление элементарного векторного нуля, и сложение и разложение векторов по правилу параллелограмма.

Рисунок 20
Критерий эквивалентности – две системы скользящих векторов эквивалентны в том и только в том случае, если равны их главные векторы и главные моменты относительно произвольно выбранного полюса.
Лемма. Произвольная система векторов может быть приведена к двум векторам, один из которых приложен к произвольной точке.

Рисунок 21
Приведение системы скользящих векторов к выбранному полюсу:

Рисунок 22
Просто перенести скользящий вектор без добавления пары (момента) мы не можем.
Рассмотрим все возможные случаи приведенных систем скользящих векторов:
1.
 (винт)
(винт)
Проекция
 неизменна, т.к. является вторым инвариантом,
т.е. проекцией главного момента на
главный вектор.
неизменна, т.к. является вторым инвариантом,
т.е. проекцией главного момента на
главный вектор.
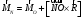

 плоскости
плоскости

Найдется
такая точка
 ,
что
,
что
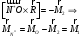

Рисунок 23
Предположим,
есть еще такая точка
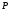 :
:

Тогда
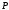 должна лежать на параллели
должна лежать на параллели
 и проходить через
и проходить через
 .
На линии, проходящей через
.
На линии, проходящей через
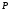 и
и
 ,
главный момент будет иметь минимальное
значение. При этом главный момент равен
,
главный момент будет иметь минимальное
значение. При этом главный момент равен
 ,
и называется моментом
винта.
,
и называется моментом
винта.
Другими словами, приводя систему векторов к виду, при котором главный вектор и главный момент параллельны, мы приводим систему векторов к винту.

Рисунок 24
Также говорят, приводим систему скользящих векторов к простейшему виду.

Рисунок 25
Найдем уравнение оси минимальных моментов из условия параллельности главного момента и главного вектора.
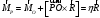

- векторная запись уравнения оси минимальных моментов.

Тогда,
 ,
,
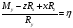 ,
,


Координатная запись уравнения оси минимальных моментов.
2.
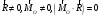 (равнодействующая)
(равнодействующая)
Систему
характеризует только один инвариант,
 - равнодействующая, к которой система
сводится.
- равнодействующая, к которой система
сводится.
К
данному случаю относится также вариант


3.
 (равнодействующая пара)
(равнодействующая пара)
Чистое поворачивающее усилие:

4.
 (равновесие)
(равновесие)
|
Случай |
Теория скользящих векторов |
Кинематика |
|
|
Винт |
Кинематический винт |
|
|
Равнодействующая |
Вращение |
|
|
Равнодействующая пара |
Поступательное движение |
|
|
Равновесие |
Покой |

Пример.

Рисунок 26

Т.е. момент угловой скорости является скоростью.
В
кинематике
 соответствует
соответствует
 ,
а
,
а
 соответствует
соответствует
 .
.
Пример.

Рисунок 27
Тело
совершает винтовой движение, а другое
тело вращается относительно оси
 .
.
Найти простейший вид относительного движения первого тела относительно второго.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,



Если
 - чистое вращение.
- чистое вращение.
Если
 - винтовое движение.
- винтовое движение.
Уравнение оси минимальных моментов:

Отсюда,

 ,
,

16
До сих пор мы рассматривали геометрию движения, не вникая в причины. Теперь движение будет рассмотрено в причинно-следственной связи. Существует две задачи динамики:
-
По движению определить силы;
-
По силам определить движение.
В основном делается акцент на второй задаче.
В качестве постулатов динамики выступают:
Три закона Ньютона,
Принцип независимости действия сил,
Принцип освобождаемости от связей.
С первыми двумя вы уже знакомы, о последнем – подробней.
Движущиеся объекты испытывают ограничения. Тела и поверхности, ограничивающие это движение, называются связями, а силы – реакциями связей.
Принцип освобождаемости от связей гласит:
Всякое несвободное тело можно рассматривать как свободное, если отбросить их связи и заменить их реакциями.
Примеры.
На гладкой и шероховатой поверхности находится тело.

Рисунок 28
Можно выделить следующие реакции:
Реакцию по нормали к поверхности и реакцию шероховатой поверхности при наличии активных сил в касательном направлении.
Экспериментальный закон Кулона относительно предельной силы трения гласит:
 .
.
До
начала движения при
 округлое тело либо находится в покое,
либо катится без проскальзывания.
Считается, что при скольжении
округлое тело либо находится в покое,
либо катится без проскальзывания.
Считается, что при скольжении
 сохраняется, хотя в начальный момент
она больше
сохраняется, хотя в начальный момент
она больше
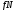 .
.
 - коэффициент трения
не зависит от величины поверхности
соприкосновения тел и определяется
материалом и качеством обработки. Есть
таблицы коэффициентов трения
- коэффициент трения
не зависит от величины поверхности
соприкосновения тел и определяется
материалом и качеством обработки. Есть
таблицы коэффициентов трения
 .
В задачах
.
В задачах
 задан или подлежит определению.
задан или подлежит определению.
Еще один пример связи – шарнир. Шарнир состоит из втулки и пальца шарнира.

Рисунок 29
Шарнир в виде цилиндра имеет две неизвестных компоненты силы реакции, в виде шара – три.
Блок – еще один тип связи. Желоб блока делают гладким.

Рисунок 30
Поскольку трения в блоке нет силы, действующие на трос по разные стороны блока, равны по величине, хотя имеют разные направления.
Еще один пример – балка в стене.
Реакция
в этом случае не определена. Шесть
неизвестных:
 .
.

Рисунок 31
Известно, что реакцию связи можно свести к двум силам, одна из которых связана с точкой.
Реакция – пассивная сила, она является следствием воздействия активных сил.
ОСНОВНЫЕ ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ
Импульс
 ,
момент
импульса
,
момент
импульса
 и кинетическая
энергия
и кинетическая
энергия
 .
.
Импульс
по определению:
 .
.
Центр масс (инерции) определяется радиус-вектором:
 ,
,
где
 - радиусы-векторы, проведенные из одного
и того же полюса.
- радиусы-векторы, проведенные из одного
и того же полюса.
Тогда,
если
 продифференцировать, то:
продифференцировать, то:

Кинетический момент по определению:

Сделаем
подсчет
 с рассмотрением сложного движения, при
этом вводится подвижная система отсчета.
с рассмотрением сложного движения, при
этом вводится подвижная система отсчета.

Рисунок 32



Пусть
система отсчета будет поступательной,
т.е.
 .
.
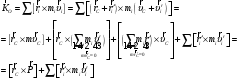
Т.е.
для системы точек
 при выборе поступательной системы
отсчета.
при выборе поступательной системы
отсчета.
В аналогичном случае для твердого тела:

Если
подставим
 ,
то:
,
то:

где
 - матрица тензора инерции.
- матрица тензора инерции.
В
случае, когда
 :
(плоско-параллельное движение, например)
:
(плоско-параллельное движение, например)

где
 - момент инерции относительно оси,
проходящей через центр инерции
- момент инерции относительно оси,
проходящей через центр инерции
 и параллельной вектору
и параллельной вектору
 ,
т.е. в этом случае
,
т.е. в этом случае

Пример.

Рисунок 33


 - момент инерции
относительно оси
- момент инерции
относительно оси
 .
.
Последнее равенство ни что иное как использование теоремы Гюйгенса-Штейнера.

Рисунок 34
Теорему Гюйгенса-Штейнера можно применять только когда есть чистое вращение, а в последнем случае – нельзя, и надо применять общую формулу:

Кинетическая энергия по определению:

 при
при


Теорема
Кёнига.
Кинетическая энергия системы точек
(твердого тела) равна кинетической
энергии движения центра масс системы
с мысленно сосредоточенной в нем массой
всех точек (твердого тела), плюс
кинетическая энергия относительного
движения относительно системы отсчета
с началом в центре масс и движущейся
поступательно.

Такую
систему еще называют кениговой. (начало
в точке
 ,
,
 )
)
Если
 ,
то
,
то

В
общем случае

Задача. (см. рис. 48)
 ,
,
 ,
,
 ,
,