
- •(И особенно на потоке в.Т.Петровой)
- •1. Ранг матрицы, определитель матрицы
- •2. Системы линейных уравнений
- •2. Линейные пространства
- •3. Линейные отображения линейных пространств
- •4. Эндоморфизмы линейных пространств
- •5. Линейные формы на линейных пространствах
- •6. Билинейные и квадратичные формы на линейных пространствах
- •7. Скалярное произведение. Евклидово линейное пространство
- •8. Линейные операторы на евклидовых линейных пространствах
- •9. Квадратичные формы на евклидовых линейных пространствах
8. Линейные операторы на евклидовых линейных пространствах
Почему матрица ортогонального оператора в ортонормированном базисе евклидова линейного пространства
 ортогональная?
ортогональная?Может ли матрица ортогонального оператора на конечномерном евклидовом линейном пространстве
 ,
быть не ортогональной в каком-либо его
базисе?
,
быть не ортогональной в каком-либо его
базисе?Может ли ортогональный эндоморфизм линейного пространства быть вырожденным?
Является ли ортогональный эндоморфизм линейного пространства его автоморфизмом
Если
 – ортогональные автоморфизмы линейного
евклидова пространства
– ортогональные автоморфизмы линейного
евклидова пространства ,
т.е.
,
т.е. O
O ,
то ортогонален ли автоморфизм
,
то ортогонален ли автоморфизм ?
?**Образует ли множество всех ортогональных эндоморфизмов O
 евклидова линейного пространства
евклидова линейного пространства группу относительно операции их
композиции?
группу относительно операции их
композиции?Линейное пространство
 рассматривается со стандартным скалярным
произведением. Ортогонален ли
автоморфизмом
рассматривается со стандартным скалярным
произведением. Ортогонален ли
автоморфизмом (поворот векторной плоскости
(поворот векторной плоскости на угол
на угол )?
)?Линейное пространство
 рассматривается со стандартным скалярным
произведением. Ортогонален ли
эндоморфизмом
рассматривается со стандартным скалярным
произведением. Ортогонален ли
эндоморфизмом (центральная симметрия векторной
плоскости
(центральная симметрия векторной
плоскости )?
)?Линейное пространство
 рассматривается со стандартным скалярным
произведением. Ортогонален ли
автоморфизмом
рассматривается со стандартным скалярным
произведением. Ортогонален ли
автоморфизмом (ортогональное отражение векторной
плоскости
(ортогональное отражение векторной
плоскости относительно векторной прямой
(одномерного подпространства)
относительно векторной прямой
(одномерного подпространства) )?
)?Линейное пространство
 рассматривается со стандартным скалярным
произведением. Являются ли ортогональным
эндоморфизмом
рассматривается со стандартным скалярным
произведением. Являются ли ортогональным
эндоморфизмом –
ортогональное проектирование векторной
плоскости
–
ортогональное проектирование векторной
плоскости на векторную прямую
на векторную прямую ?
?Является ли ортогональное проектирование евклидова линейного пространства на его любое нетривиальное подпространство ортогональным линейным оператором?
**
 – ортогональный оператор конечномерного
евклидова линейного пространства
– ортогональный оператор конечномерного
евклидова линейного пространства ,
т.е.
,
т.е. O
O и все элементы его матрицы
и все элементы его матрицы
 в ортонормированном базисе этого
пространства равны по модулю. Можно ли
указать значение этой абсолютной
величины?
в ортонормированном базисе этого
пространства равны по модулю. Можно ли
указать значение этой абсолютной
величины? –ортогональный
оператор конечномерного евклидова
линейного пространства
–ортогональный
оператор конечномерного евклидова
линейного пространства
 ,
т.е.
,
т.е. O
O .
Является ли его матрица относительно
любого базиса этого пространства
ортогональной?
.
Является ли его матрица относительно
любого базиса этого пространства
ортогональной? –ортогональный
оператор конечномерного евклидова
линейного пространства
–ортогональный
оператор конечномерного евклидова
линейного пространства
 ,
т.е.
,
т.е.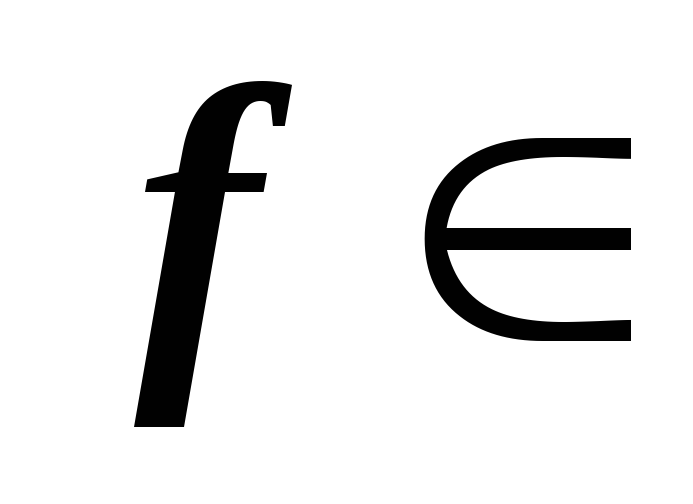 O
O .
Является ли он автоморфизмом (обратимым
эндоморфизмом) этого линейного
пространства
.
Является ли он автоморфизмом (обратимым
эндоморфизмом) этого линейного
пространства
 ?
?Может ли число
 быть собственным значением ортогонального
линейного оператора
быть собственным значением ортогонального
линейного оператора O
O евклидова линейного пространства
евклидова линейного пространства
 ?
?Может ли число
 быть собственным значением ортогонального
линейного оператора
быть собственным значением ортогонального
линейного оператора O
O евклидова линейного пространства
евклидова линейного пространства
 ?
?*Пусть
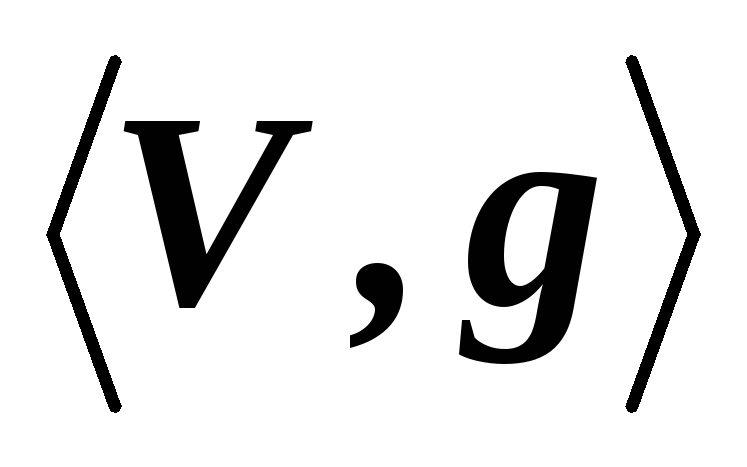 – евклидово линейное пространство, а
– евклидово линейное пространство, а O
O – ортогональный оператор этого
пространства имеет инвариантное
подпространство
– ортогональный оператор этого
пространства имеет инвариантное
подпространство
 .
Верно ли, что
.
Верно ли, что –
ортогональное дополнение
–
ортогональное дополнение также инвариантно относительно
также инвариантно относительно ?
?*Пусть
 –конечномерное
евклидово
линейное пространство, а
–конечномерное
евклидово
линейное пространство, а
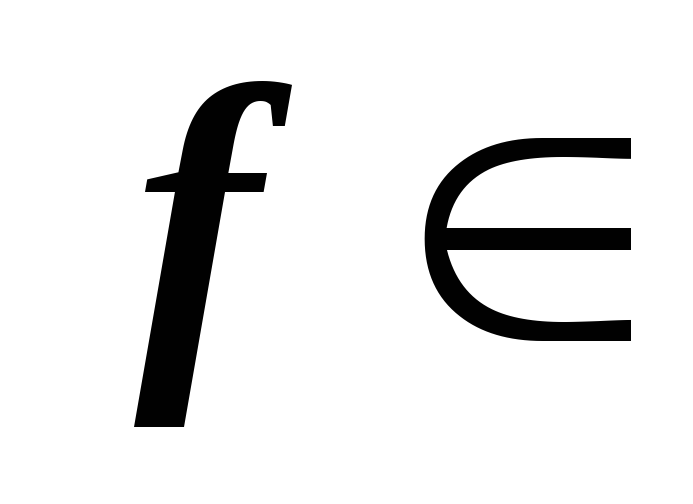 O
O – ортогональный оператор этого
пространства имеет инвариантное
подпространство
– ортогональный оператор этого
пространства имеет инвариантное
подпространство
 .
Верно ли, что
.
Верно ли, что –
ортогональное дополнение
–
ортогональное дополнение также инвариантно относительно
также инвариантно относительно ?
?Векторная плоскость
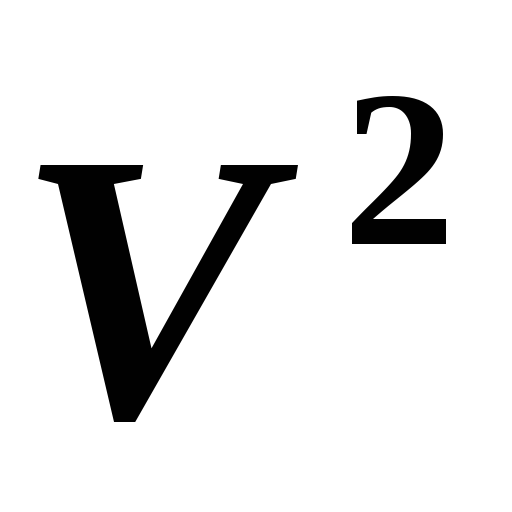 рассматривается со стандартным скалярным
произведением,
рассматривается со стандартным скалярным
произведением, O
O (
( –
центральная симметрия
–
центральная симметрия ).
Найдите эндоморфизм, сопряженный
).
Найдите эндоморфизм, сопряженный .
.Векторная плоскость
 рассматривается со стандартным скалярным
произведением,
рассматривается со стандартным скалярным
произведением, O
O (
( –
ортогональное отражение
–
ортогональное отражение относительно векторной прямой
(одномерного подпространства)
относительно векторной прямой
(одномерного подпространства) ).
Найдите эндоморфизм, сопряженный
).
Найдите эндоморфизм, сопряженный .
.Векторная плоскость
 рассматривается со стандартным скалярным
произведением,
рассматривается со стандартным скалярным
произведением, O
O (
( –
ортогональное проектирование
–
ортогональное проектирование на векторную прямую
на векторную прямую ).
Найдите эндоморфизм, сопряженный
).
Найдите эндоморфизм, сопряженный .
.*Векторная плоскость
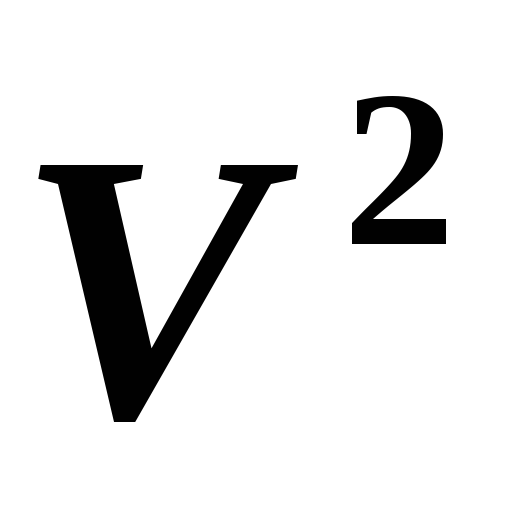 рассматривается со стандартным скалярным
произведением,
рассматривается со стандартным скалярным
произведением, O
O (
( –
поворот
–
поворот на угол
на угол ).
Найдите эндоморфизм, сопряженный
).
Найдите эндоморфизм, сопряженный .
.Векторная плоскость
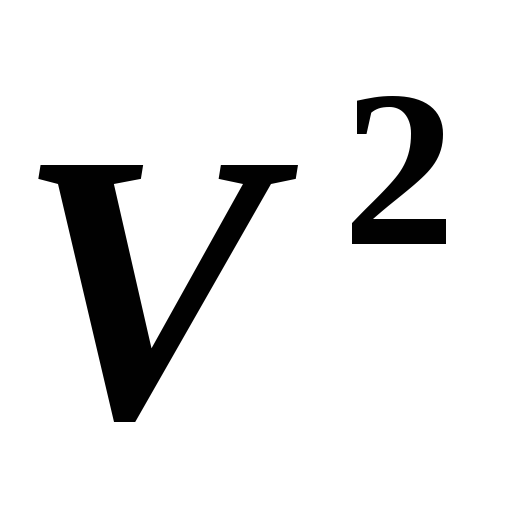 рассматривается со стандартным скалярным
произведением,
рассматривается со стандартным скалярным
произведением, (
( –
гомотетия
–
гомотетия с коэффициентом
с коэффициентом ).
Найдите эндоморфизм, сопряженный
).
Найдите эндоморфизм, сопряженный .
.*Пусть
 – евклидово линейное пространство, а
– евклидово линейное пространство, а .
Его подпространство
.
Его подпространство инвариантно относительно
инвариантно относительно .
Верно ли, что
.
Верно ли, что –
ортогональное дополнение
–
ортогональное дополнение инвариантно относительно сопряженного
инвариантно относительно сопряженного эндоморфизма
эндоморфизма ?
?*Пусть
 –конечномерное
евклидово линейное пространство, а
–конечномерное
евклидово линейное пространство, а
 .
Его подпространство
.
Его подпространство инвариантно относительно
инвариантно относительно .
Верно ли, что
.
Верно ли, что –
ортогональное дополнение
–
ортогональное дополнение инвариантно относительно сопряженного
инвариантно относительно сопряженного эндоморфизма
эндоморфизма ?
?*Пусть
 – евклидово линейное пространство, а
для отображения
– евклидово линейное пространство, а
для отображения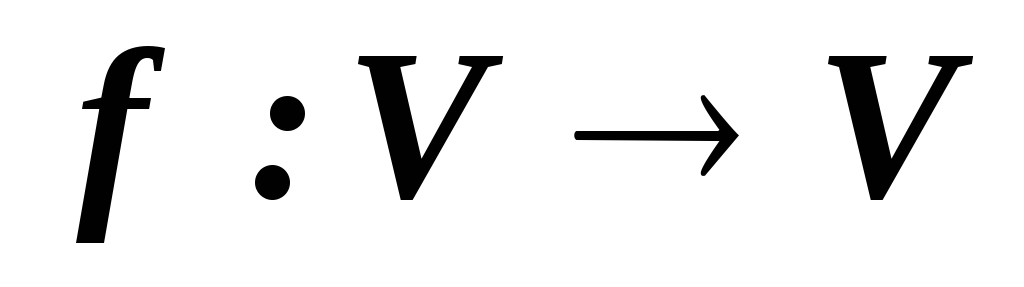 существует
отображение
существует
отображение такое, что
такое, что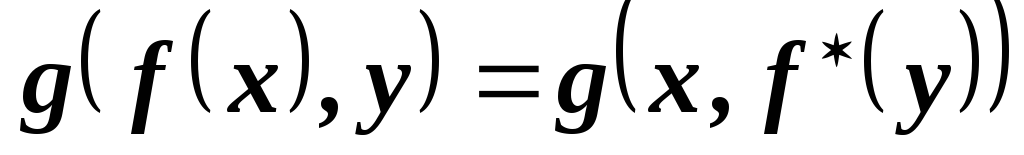 для любых векторов
для любых векторов .
Докажите, что
.
Докажите, что .
.Пусть
 – евклидово линейное пространство,
– евклидово линейное пространство, и является самосопряженным оператором
с простым спектром. Сколько различных
(не гомотетичных) базисов можно составить
его собственных векторов?
и является самосопряженным оператором
с простым спектром. Сколько различных
(не гомотетичных) базисов можно составить
его собственных векторов?Пусть
 – евклидово линейное пространство,
– евклидово линейное пространство, ,
а
,
а –
его сопряженный оператор. Найдите и
сравните их характеристические
многочлены
–
его сопряженный оператор. Найдите и
сравните их характеристические
многочлены и
и ,
сравните собственные значения
,
сравните собственные значения и
и .
.Можно ли по характеристическому уравнению линейного оператора найти собственные значения сопряженного ему линейного оператора?
Может ли быть вырожденным самосопряженный оператор на линейном пространстве?
Почему матрица самосопряженного оператора
 S
S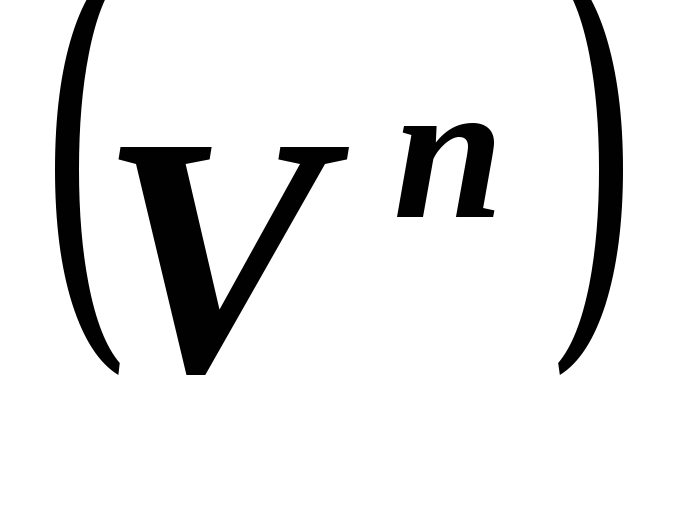 в ортонормированном
базисе евклидова линейного пространства
в ортонормированном
базисе евклидова линейного пространства
 симметрическая?
симметрическая?Базис
 конечномерного линейного евклидова
пространства
конечномерного линейного евклидова
пространства не является ортонормированным
относительно скалярного произведения
не является ортонормированным
относительно скалярного произведения .
. и имеет
и имеет матрицей относительно
матрицей относительно .
Укажите матрицу
.
Укажите матрицу сопряженного
сопряженного эндоморфизма.
эндоморфизма.* Пусть
 – евклидово линейное пространство,
– евклидово линейное пространство, –
его подпространство.
–
его подпространство. –
ортогональное проектирование
–
ортогональное проектирование на подпространство.
Укажите сопряженный
на подпространство.
Укажите сопряженный
 линейный оператор.
линейный оператор.Векторная плоскость
 рассматривается со стандартным скалярным
произведением. Является ли центральная
симметрия
рассматривается со стандартным скалярным
произведением. Является ли центральная
симметрия O
O пространства
пространства
 самосопряженным оператором на
самосопряженным оператором на ?
?Векторная плоскость
 рассматривается со стандартным скалярным
произведением. Является ли ортогональное
отражение
рассматривается со стандартным скалярным
произведением. Является ли ортогональное
отражение O
O пространства
пространства
 относительно векторной прямой
относительно векторной прямой самосопряженным оператором на
самосопряженным оператором на ?
?Векторная плоскость
 рассматривается со стандартным скалярным
произведением. Является ли ортогональное
проектирование
рассматривается со стандартным скалярным
произведением. Является ли ортогональное
проектирование
 O
O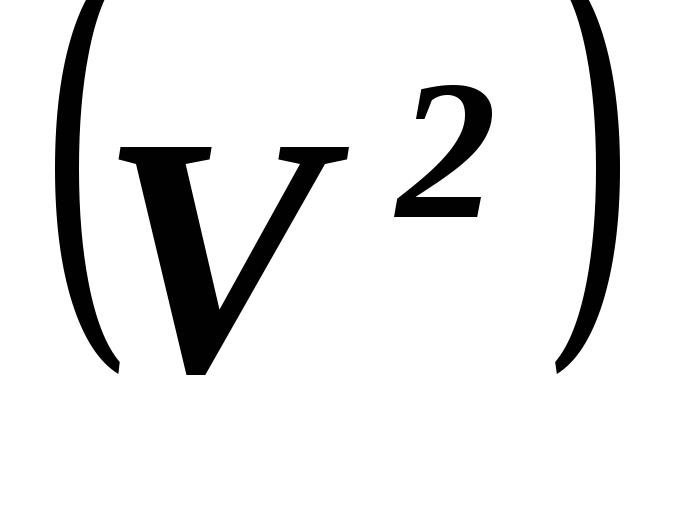 пространства
пространства
 на векторную прямую
на векторную прямую
 самосопряженным оператором на
самосопряженным оператором на
 ?
?Векторная плоскость
 рассматривается со стандартным скалярным
произведением. Является ли
рассматривается со стандартным скалярным
произведением. Является ли O
O ,поворот
,поворот
 на угол
на угол ,
самосопряженным оператором на
,
самосопряженным оператором на ?
?Векторная плоскость
 рассматривается со стандартным скалярным
произведением. Является ли
рассматривается со стандартным скалярным
произведением. Является ли ,
гомотетия
,
гомотетия с коэффициентом
с коэффициентом ,
самосопряженным оператором на
,
самосопряженным оператором на ?
?*Пусть
 – евклидово линейное пространство,
– евклидово линейное пространство, –
его подпространство. Является ли
–
его подпространство. Является ли
 ортогональное проектирование
ортогональное проектирование на подпространство
на подпространство самосопряженным линейным оператором?
самосопряженным линейным оператором?Векторная плоскость
 рассматривается со стандартным скалярным
произведением,
рассматривается со стандартным скалярным
произведением, (
( –
гомотетия
–
гомотетия с коэффициентом
с коэффициентом ).
Является ли гомотетия
).
Является ли гомотетия самосопряженным линейным оператором
на
самосопряженным линейным оператором
на ?
?*Пусть
 – евклидово линейное пространство,
– евклидово линейное пространство, –
его подпространство.
–
его подпространство.
 ортогональное проектирование
ортогональное проектирование на подпространство
на подпространство самосопряженным линейным оператором
на пространстве
самосопряженным линейным оператором
на пространстве ?
?**На линейном пространстве
 дифференцируемых и интегрируемых на
отрезке
дифференцируемых и интегрируемых на
отрезке функций со скалярное произведение
заданно формулой:
функций со скалярное произведение
заданно формулой: .
Найдите оператор, сопряженный
дифференцированию функций относительно
этого скалярного произведения.
.
Найдите оператор, сопряженный
дифференцированию функций относительно
этого скалярного произведения.**На линейном пространстве
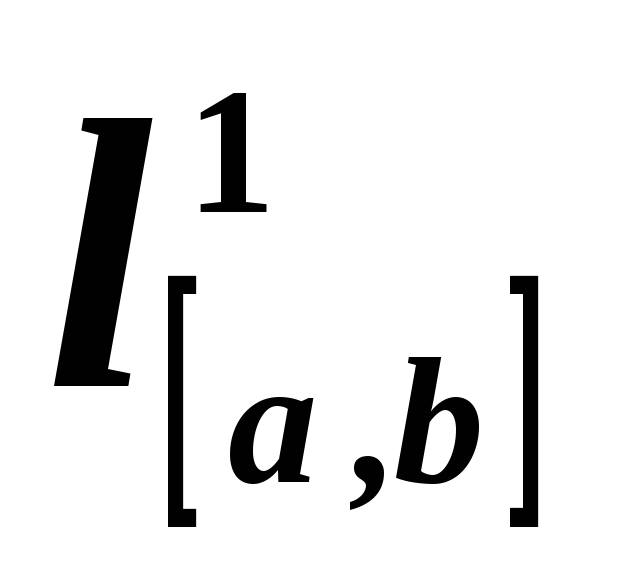 дифференцируемых и интегрируемых на
отрезке
дифференцируемых и интегрируемых на
отрезке функций со скалярное произведение
заданно формулой:
функций со скалярное произведение
заданно формулой: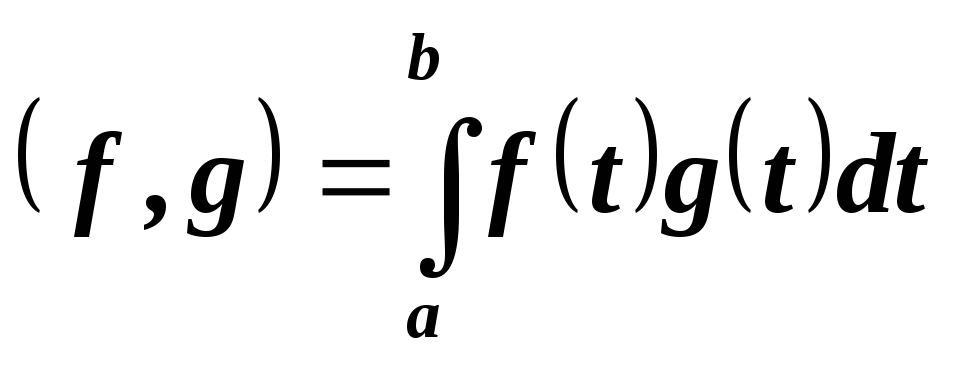 .
Найдите оператор, сопряженный
интегрированию функций относительно
этого скалярного произведения.
.
Найдите оператор, сопряженный
интегрированию функций относительно
этого скалярного произведения. –матрица линейного
оператора
–матрица линейного
оператора
 евклидова линейного пространства
евклидова линейного пространства вортонормированном
базисе. Как определить матрицу
сопряженного ему линейного оператора
в этом же базисе?
вортонормированном
базисе. Как определить матрицу
сопряженного ему линейного оператора
в этом же базисе?  –матрица линейного
оператора
–матрица линейного
оператора
 евклидова линейного пространства
евклидова линейного пространства впроизвольном
базисе. Какова
матрица сопряженного ему оператора?
впроизвольном
базисе. Какова
матрица сопряженного ему оператора? Как изменится матрица ортогонального оператора
 O
O на евклидовом линейном пространстве
на евклидовом линейном пространстве
 ,
если от его ортонормированного базиса
,
если от его ортонормированного базиса перейти к базису
перейти к базису ?
?Как изменится матрица оператора
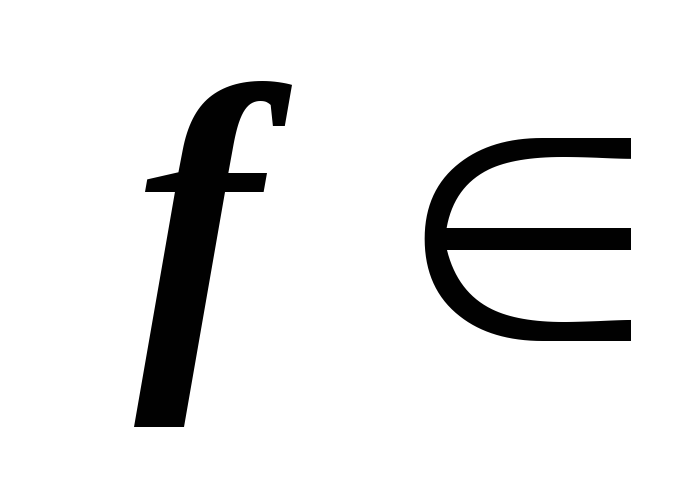 O
O на евклидовом линейном пространстве
на евклидовом линейном пространстве
 ,
если от его ортонормированного базиса
,
если от его ортонормированного базиса перейти к базису
перейти к базису с матрицей перехода
с матрицей перехода ?
Будет ли матрица
?
Будет ли матрица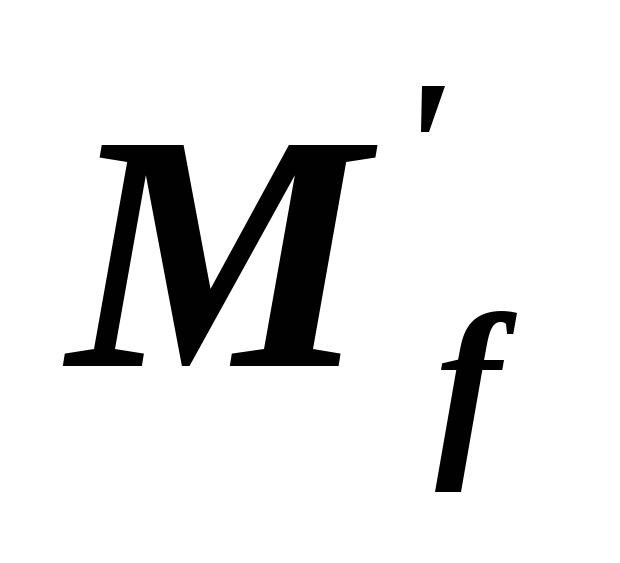 оператора
оператора в базисе
в базисе ортогональной, если этот базис не
ортонормирован относительно
ортогональной, если этот базис не
ортонормирован относительно ?
?Пусть
 O
O ,
где
,
где
 – двумерное евклидово линейное
пространство, и матрица
– двумерное евклидово линейное
пространство, и матрица оператора
оператора ортогональна в базисе
ортогональна в базисе ,
ортонормированном относительно
,
ортонормированном относительно .
Будет ли в базисе
.
Будет ли в базисе ортогональной матрица
ортогональной матрица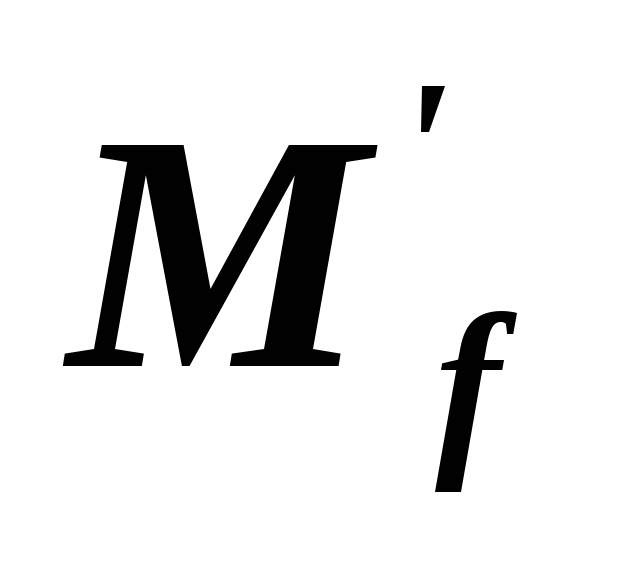 ?
?Может ли
 ,
где
,
где – двумерное евклидово линейное
пространство, быть одновременно и
ортогональным и самосопряженным?
– двумерное евклидово линейное
пространство, быть одновременно и
ортогональным и самосопряженным?*Может ли самосопряженный оператор на линейном пространстве быть ортогональным? В случае положительного ответа приведите примеры.
*Среди ортогональных операторов
 O
O укажите все самосопряженные или
докажите, что таких не существует.
укажите все самосопряженные или
докажите, что таких не существует.*Может ли самосопряженный оператор на линейном пространстве быть вырожденным? В случае положительного ответа приведите примеры.
Всегда ли самосопряженный оператор линейного пространства является его автоморфизмом
Если
 – самосопряженные операторы линейного
евклидова пространства
– самосопряженные операторы линейного
евклидова пространства ,
т.е.
,
т.е.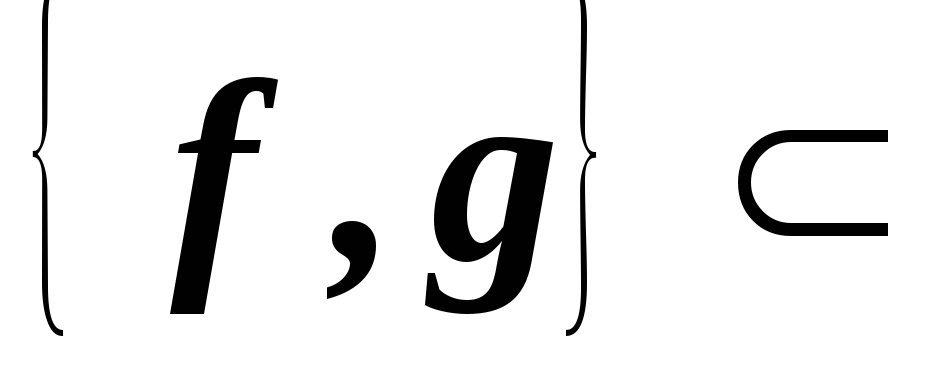 S
S .
Верно ли, что оператор
.
Верно ли, что оператор тоже самосопряженный?
тоже самосопряженный?Докажите, что операция сопряжения линейного оператора в евклидовом линейном пространстве обладает свойством:
 .
.**Образует ли множество всех самосопряженных операторов на евклидовом линейном пространстве S
 группу относительно
операции их композиции?
группу относительно
операции их композиции?*Верно ли для любого
 O
O ,
что
,
что
 ?
?*Верно ли, что для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве выполняется
выполняется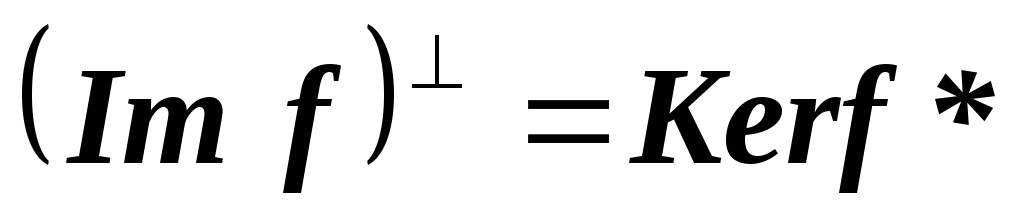 ?
?*Верно ли, что для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве выполняется
выполняется ?
?Верно ли, что если
 S
S – самосопряженный оператор евклидова
линейного пространства
– самосопряженный оператор евклидова
линейного пространства
 имеет инвариантное подпространство
имеет инвариантное подпространство ,
то его ортогональное дополнение
,
то его ортогональное дополнение также инвариантно относительно
также инвариантно относительно ?
?*Верно ли для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве утверждение
утверждение ?
?*Верно ли для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве утверждение
утверждение ?
?*Верно ли для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве утверждение
утверждение ?
?*Верно ли для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве утверждение
утверждение ?
?*Верно ли для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве ,
что
,
что самосопряженный линейный оператор?
самосопряженный линейный оператор?*Верно ли для любого линейного оператора
 ,
где
,
где –
евклидово линейное пространство, что
–
евклидово линейное пространство, что самосопряженный линейный оператор?
самосопряженный линейный оператор?*Верно ли для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве ,
что
,
что ортогональный линейный оператор?
ортогональный линейный оператор?*Верно ли для любого линейного оператора
 на евклидовом линейном пространстве
на евклидовом линейном пространстве ,
что
,
что ортогональный линейный оператор?
ортогональный линейный оператор?**Верно ли для любого линейного оператора
 евклидова линейного пространства
евклидова линейного пространства утверждение: если уравнение
утверждение: если уравнение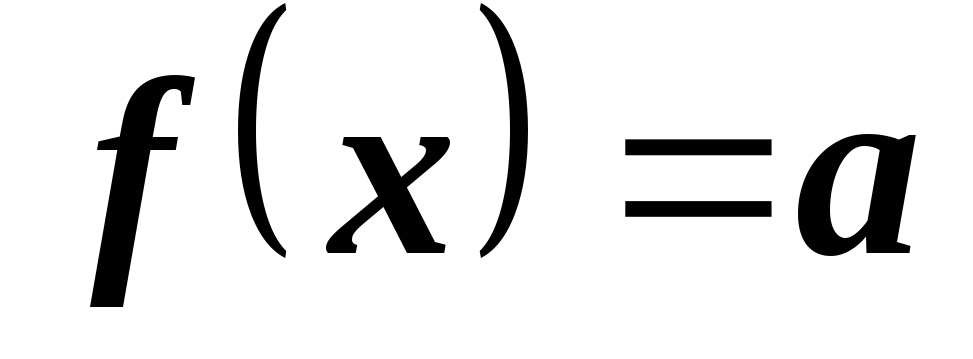 имеет решение, то всякое его решение
удовлетворяет уравнению
имеет решение, то всякое его решение
удовлетворяет уравнению ?
?Пусть
 ,
а
,
а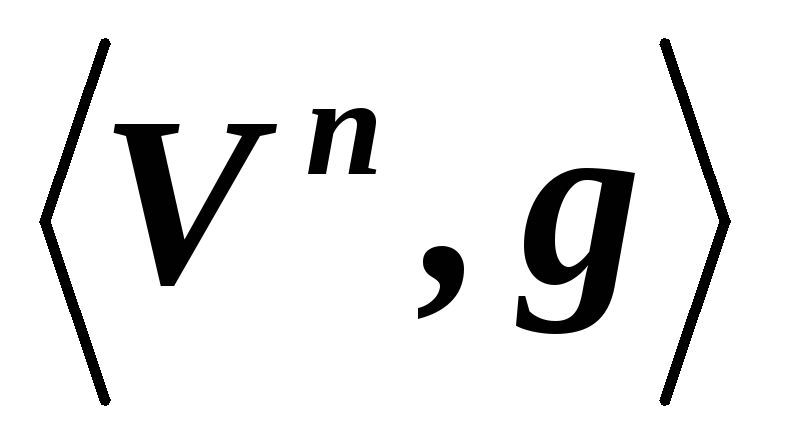 – конечномерное евклидово линейное
пространство и в некотором базисе имеет
матрицей симметрическую матрицу
– конечномерное евклидово линейное
пространство и в некотором базисе имеет
матрицей симметрическую матрицу .
Верно ли, что
.
Верно ли, что S
S –самосопряженный
на пространстве
–самосопряженный
на пространстве
 ?
?Как связаны между собой собственные значения линейных операторов
 и
и ,
если эти операторы действуют в унитарном
линейном пространстве?
,
если эти операторы действуют в унитарном
линейном пространстве?Верно ли, что оператор
 ,
где
,
где – евклидово линейное пространство,
всегда имеет инвариантное
гиперподпространство (подпространство
размерности
– евклидово линейное пространство,
всегда имеет инвариантное
гиперподпространство (подпространство
размерности )?
)?*
 ,
где
,
где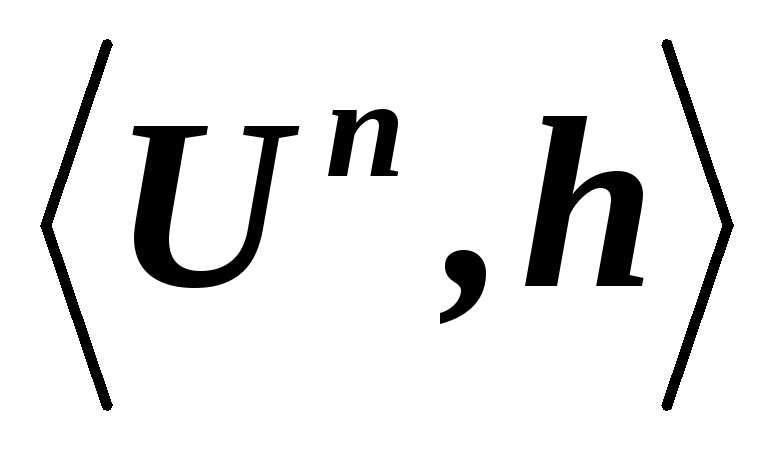 –
унитарное линейное пространство. Верно
ли, что этот оператор всегда имеет
инвариантное гиперподпространство
(подпространство размерности
–
унитарное линейное пространство. Верно
ли, что этот оператор всегда имеет
инвариантное гиперподпространство
(подпространство размерности )?
)?**Верно ли, что для любого линейного оператора
 -мерного
евклидова линейного пространства
-мерного
евклидова линейного пространства найдется базис, в котором матрица этого
оператора треугольная (верхняя
треугольная)?
найдется базис, в котором матрица этого
оператора треугольная (верхняя
треугольная)?**Верно ли, что для любого линейного оператора
 -мерного
унитарного линейного пространства
-мерного
унитарного линейного пространства найдется базис, в котором матрица этого
оператора треугольная (верхняя
треугольная)?
найдется базис, в котором матрица этого
оператора треугольная (верхняя
треугольная)?Верно ли, что для любого самосопряженного линейного оператора
 вконечномерном
евклидовом линейном пространстве
вконечномерном
евклидовом линейном пространстве
 имеет место равенство:
имеет место равенство: ?
?*Верно ли, что для любого самосопряженного линейного оператора
 в евклидовом линейном пространстве
в евклидовом линейном пространстве имеет место равенство:
имеет место равенство: ?
?*Пусть евклидово линейное пространство
 .
Докажите, что проектирование этого
пространства на подпространство
.
Докажите, что проектирование этого
пространства на подпространство параллельно подпространству
параллельно подпространству является
самосопряженным тогда и только тогда,
когда эти подпространства ортогональные.
является
самосопряженным тогда и только тогда,
когда эти подпространства ортогональные.Может ли самосопряженное преобразование линейного евклидова пространства иметь неортогональный базис из его собственных векторов?
Может ли самосопряженное преобразование линейного евклидова пространства иметь неортогональный базис из его собственных векторов при условии, что все его собственные значения различные?
**Пусть
 S
S самосопряженные операторы евклидова
линейного пространства
самосопряженные операторы евклидова
линейного пространства
 с матрицами
с матрицами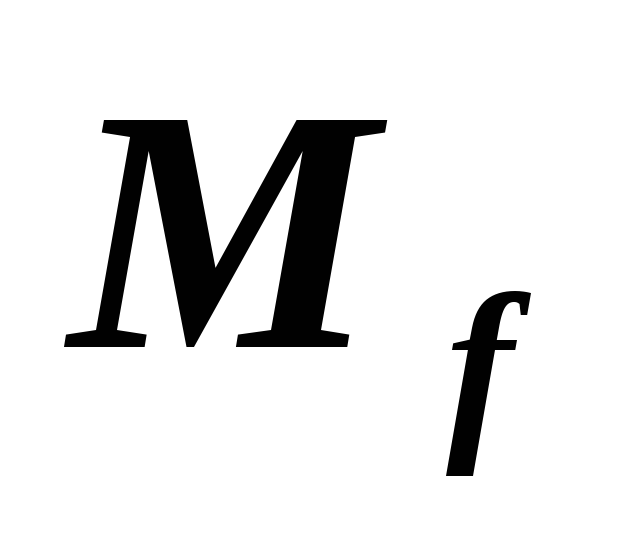 и
и ,
соответственно, относительно некоторого
ортонормированного базиса
,
соответственно, относительно некоторого
ортонормированного базиса ,причем, матрица
,причем, матрица
 положительно определена. Докажите, что
все корни характеристического уравнения
положительно определена. Докажите, что
все корни характеристического уравнения вещественные.
вещественные.**Пусть
 S
S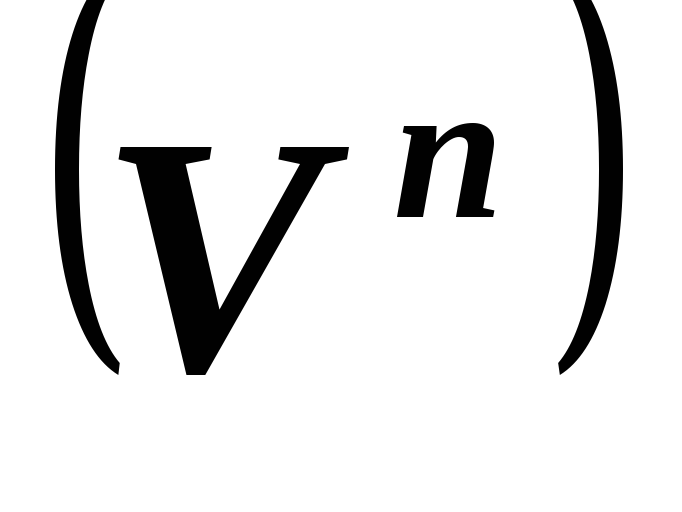 самосопряженные операторы евклидова
линейного пространства
самосопряженные операторы евклидова
линейного пространства
 с матрицами
с матрицами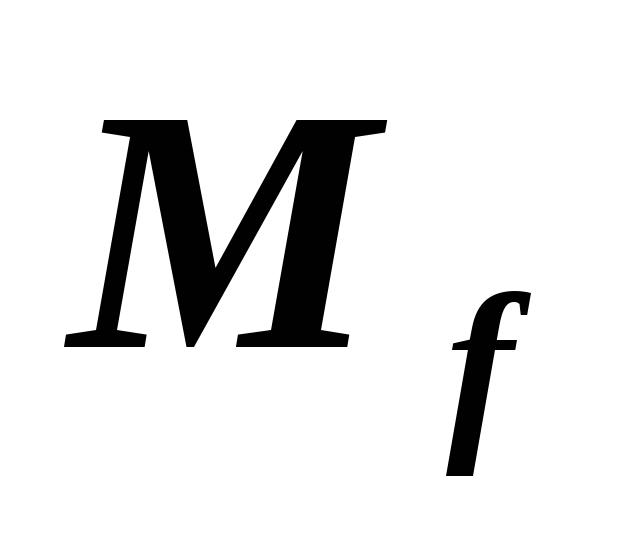 и
и ,
соответственно, относительно некоторого
ортонормированного базиса
,
соответственно, относительно некоторого
ортонормированного базиса ,причем, матрица
,причем, матрица
 положительно определена. Докажите, что
в линейном пространстве
положительно определена. Докажите, что
в линейном пространстве существует базис
существует базис ,в котором матрица
оператора
,в котором матрица
оператора  диагональная.
диагональная.**Может ли матрица самосопряженного линейного оператора линейного евклидова пространства
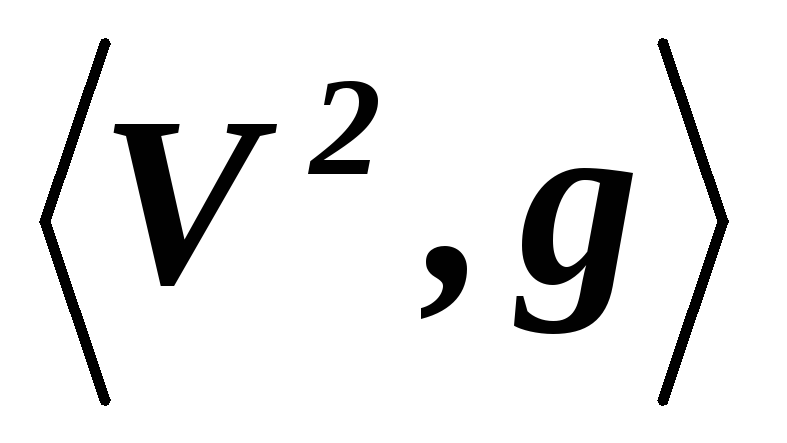 в некотором ортонормированном базисе
иметь вид:
в некотором ортонормированном базисе
иметь вид: ?
?**Может ли матрица самосопряженного линейного оператора линейного евклидова пространства
 в некотором ортонормированном базисе
иметь вид:
в некотором ортонормированном базисе
иметь вид: ?
?**Может ли матрица самосопряженного линейного оператора линейного евклидова пространства
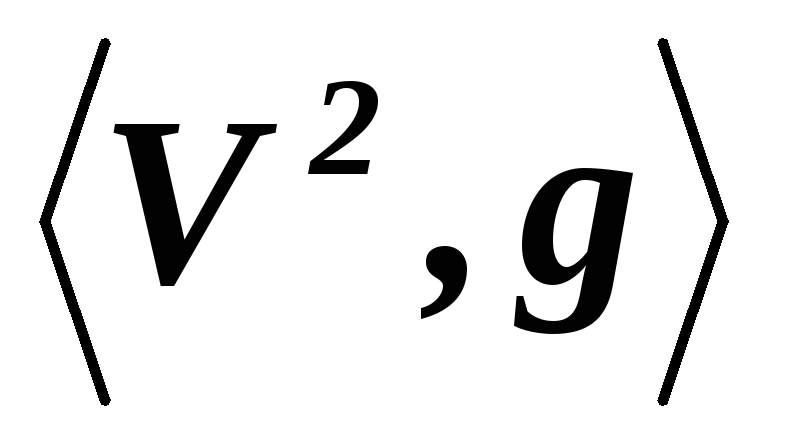 в некотором базисе иметь вид:
в некотором базисе иметь вид: ?
?**Пусть линейный оператор
 на линейном пространстве
на линейном пространстве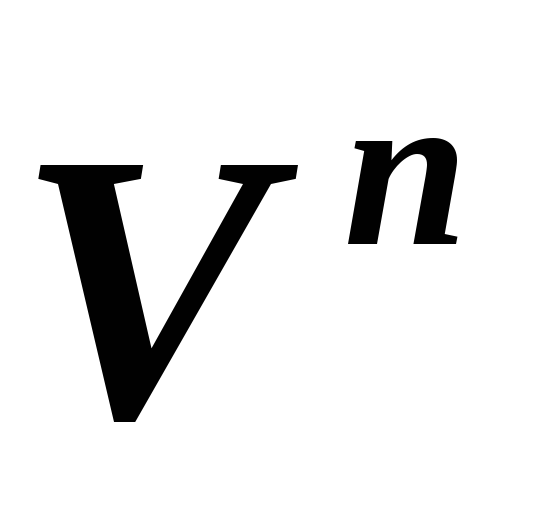 такой, что в
такой, что в есть базис из собственных векторов
есть базис из собственных векторов с вещественными собственными значениями.
Можно ли в этом
с вещественными собственными значениями.
Можно ли в этом задать скалярное произведение
задать скалярное произведение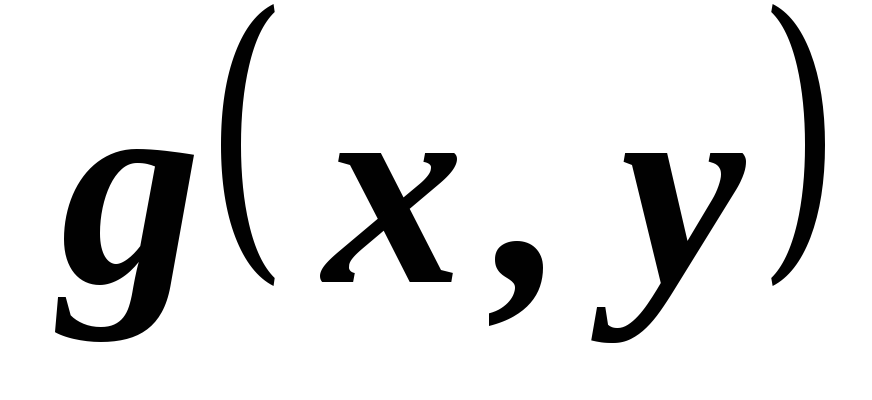 так, что относительно этого скалярного
произведения оператор
так, что относительно этого скалярного
произведения оператор будет самосопряженным?
будет самосопряженным?Докажите, что всякое линейный оператор
 на унитарном линейном пространстве
на унитарном линейном пространстве можно представить в виде суммы:
можно представить в виде суммы: ,
где
,
где и
и – эрмитовы операторы на этом пространстве.
– эрмитовы операторы на этом пространстве.Может ли линейный оператор унитарного линейного пространства
 быть одновременно и унитарным, и
эрмитовым?
быть одновременно и унитарным, и
эрмитовым?Найдите полярное разложение линейного оператора на евклидовом линейном пространстве, если известно, что его матрица в некотором ортонормированном базисе имеет вид:
 .
.Найдите полярное разложение линейного оператора на евклидовом линейном пространстве, если известно, что его матрица в некотором ортонормированном базисе имеет вид:
 .
.Найдите полярное разложение линейного оператора на евклидовом линейном пространстве, если известно, что его матрица в некотором ортонормированном базисе имеет вид:
 .
.Является ли разложение
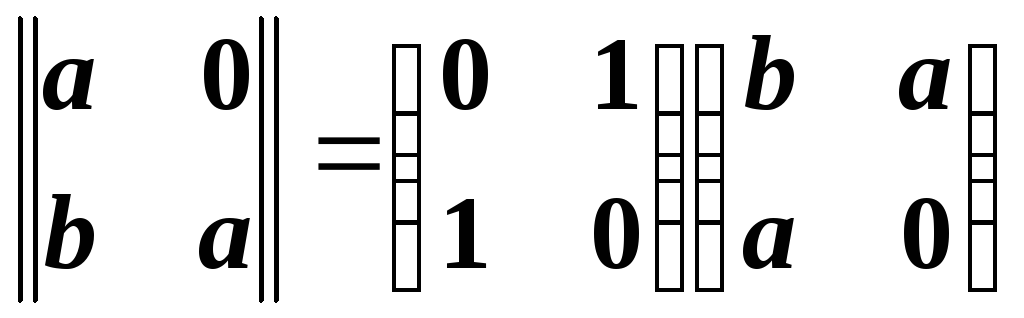 полярным разложением (
полярным разложением ( )?
)?
