
- •(И особенно на потоке в.Т.Петровой)
- •1. Ранг матрицы, определитель матрицы
- •2. Системы линейных уравнений
- •2. Линейные пространства
- •3. Линейные отображения линейных пространств
- •4. Эндоморфизмы линейных пространств
- •5. Линейные формы на линейных пространствах
- •6. Билинейные и квадратичные формы на линейных пространствах
- •7. Скалярное произведение. Евклидово линейное пространство
- •8. Линейные операторы на евклидовых линейных пространствах
- •9. Квадратичные формы на евклидовых линейных пространствах
3. Линейные отображения линейных пространств
Является ли проектирование (например, ортогональное) линейного пространства всех свободных (геометрических) векторов V
 на его одномерное подпространство
(свободных векторов, параллельных
некоторой прямой)V
на его одномерное подпространство
(свободных векторов, параллельных
некоторой прямой)V линейным отображением? В случае
положительного ответа укажите его ядро
и образ.
линейным отображением? В случае
положительного ответа укажите его ядро
и образ.Докажите, что дифференцирование
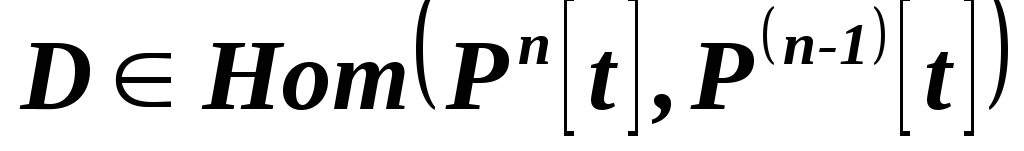 ,
где
,
где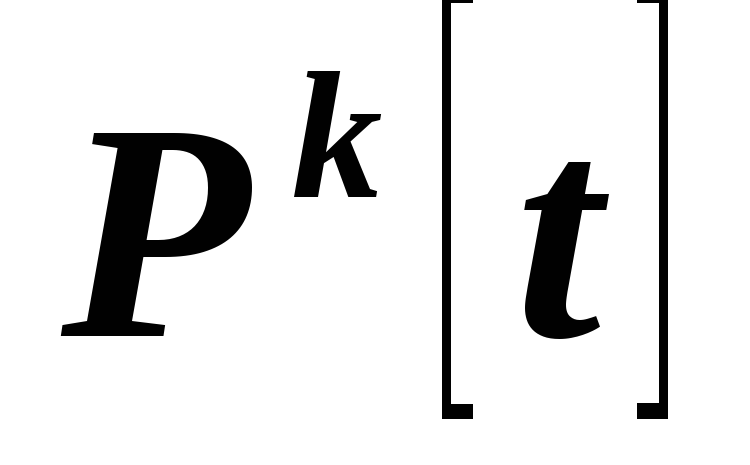 – пространство многочленов степени
не выше
– пространство многочленов степени
не выше от переменной
от переменной .
Найдите ядро и образ
.
Найдите ядро и образ .
.Докажите, что интегрирование
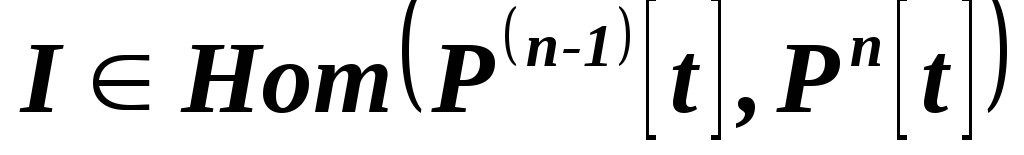 ,
где
,
где – пространство многочленов степени
не выше
– пространство многочленов степени
не выше от переменной
от переменной ,
а
,
а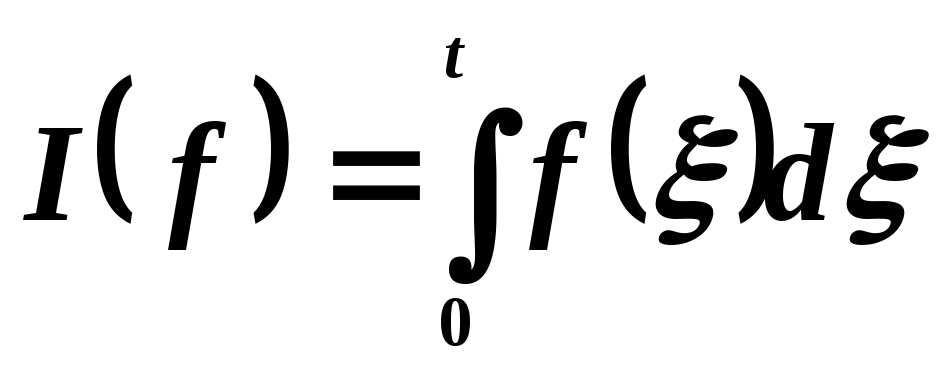 .
Найдите ядро и образ
.
Найдите ядро и образ .
.Докажите, что если
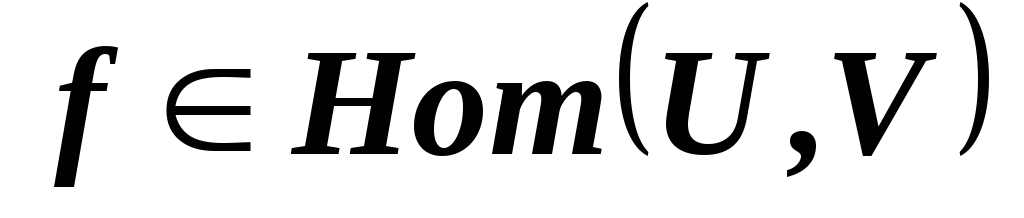 ,
то
,
то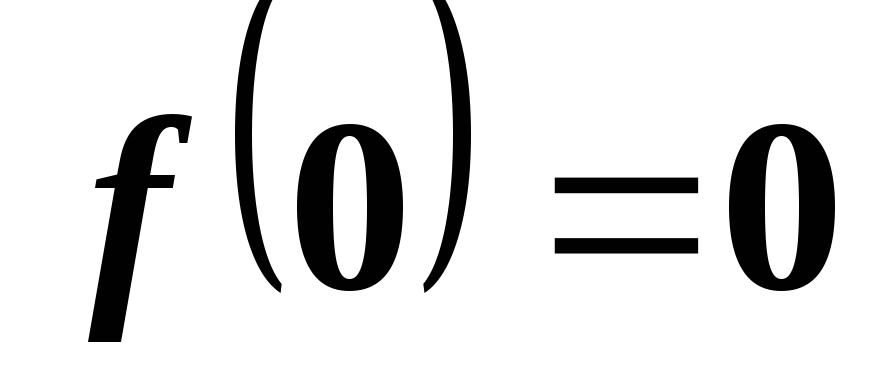 .
.Может ли при гомоморфизме линейных пространств ненулевой вектор отображаться в нулевой?
Может ли при линейном отображении система линейно зависимых векторов отображаться в линейно независимую систему векторов?
Может ли при линейном отображении система линейно независимых векторов отображаться в линейно зависимую систему векторов?
Известно, что некоторая система
 векторов линейного пространства
векторов линейного пространства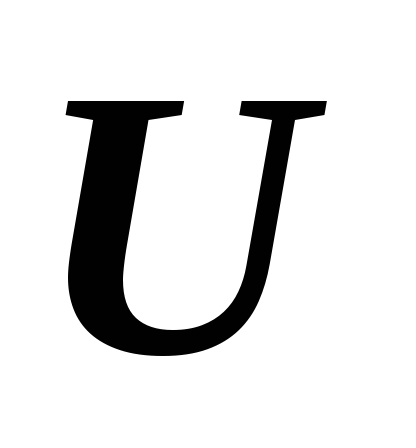 линейно независима и при линейном
отображении
линейно независима и при линейном
отображении отображается в линейно независимую
систему векторов. Следует ли из этого
свойства, что
отображается в линейно независимую
систему векторов. Следует ли из этого
свойства, что –
изоморфизм соответствующих линейных
пространств?
–
изоморфизм соответствующих линейных
пространств?*Докажите, что если линейное пространство
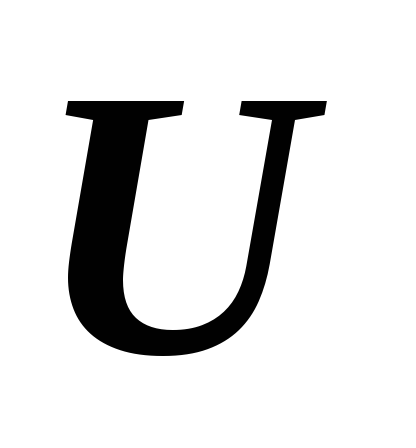 изоморфно линейному пространству
изоморфно линейному пространству ,
то линейное пространство
,
то линейное пространство изоморфно линейному пространству
изоморфно линейному пространству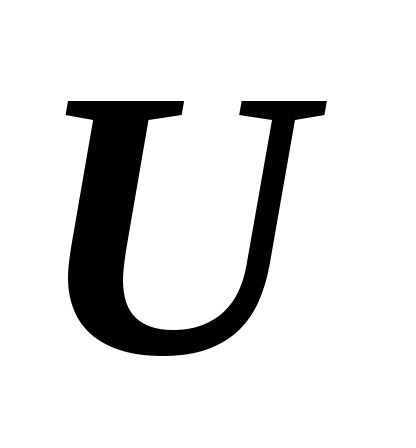 .
.*Докажите, что если линейное пространство
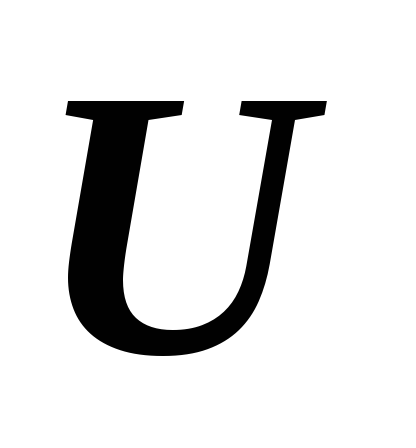 изоморфно линейному пространству
изоморфно линейному пространству ,
а линейное пространство
,
а линейное пространство изоморфно линейному пространству
изоморфно линейному пространству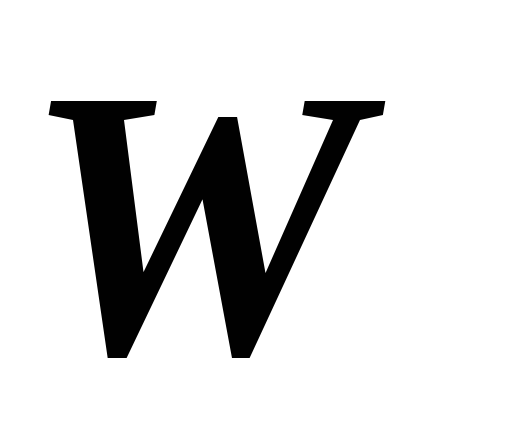 ,
то линейное пространство
,
то линейное пространство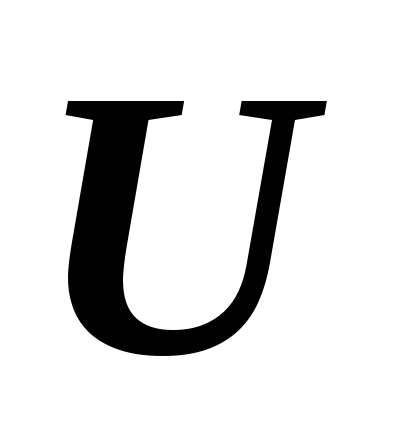 изоморфно линейному пространству
изоморфно линейному пространству .
.*
 ,
верно ли, что
,
верно ли, что ,
если
,
если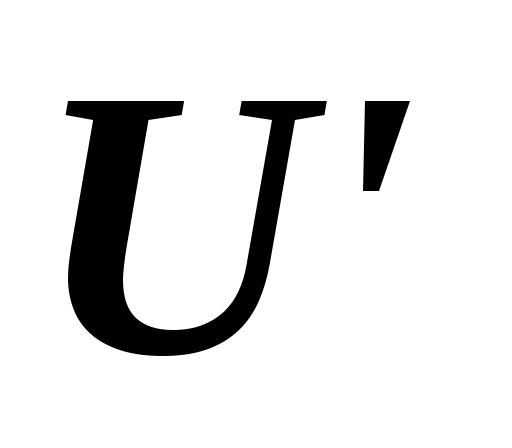 и
и –
подпространства линейного пространства
–
подпространства линейного пространства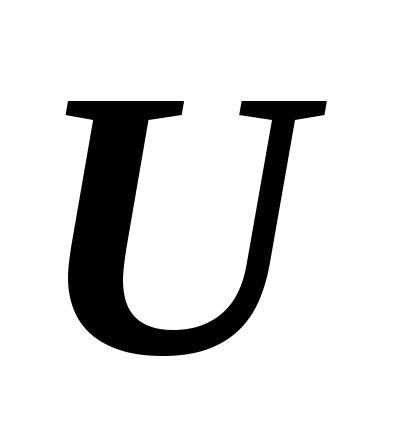 ?
?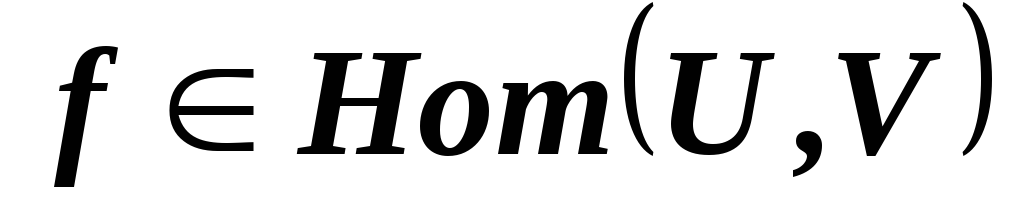 ,
верно ли, что
,
верно ли, что
 ,
если
,
если и
и –
подпространства линейного пространства
–
подпространства линейного пространства ?
?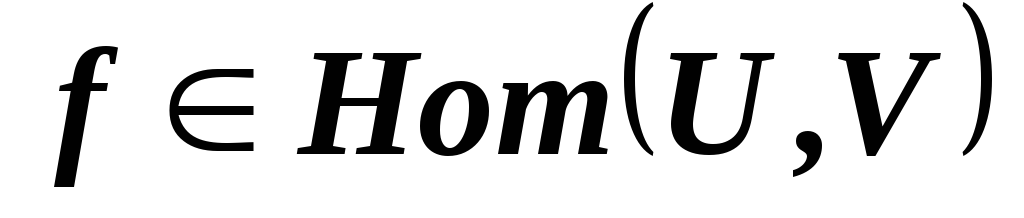 ,
верно ли, что
,
верно ли, что
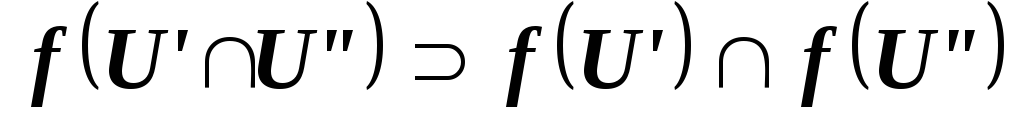 ,
если
,
если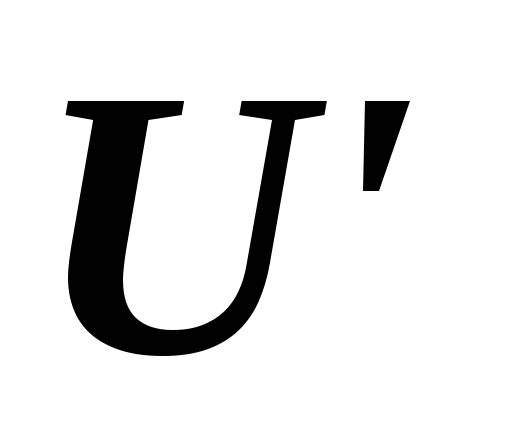 и
и –
подпространства линейного пространства
–
подпространства линейного пространства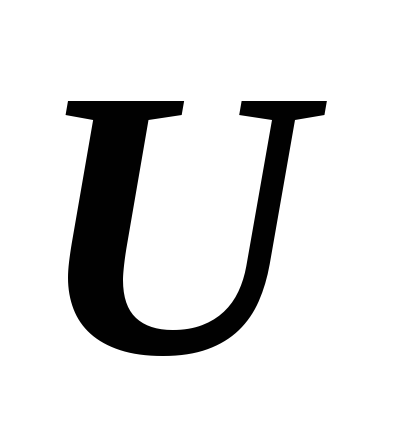 ?
?*
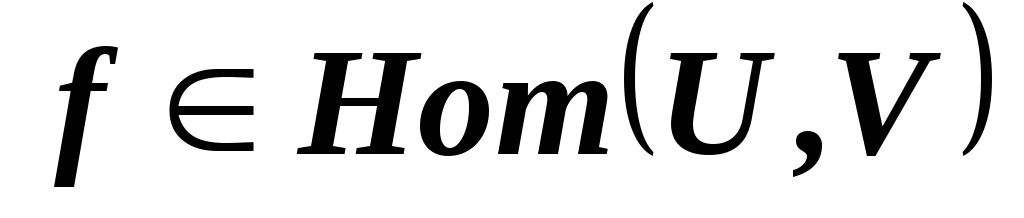 ,
верно ли, что
,
верно ли, что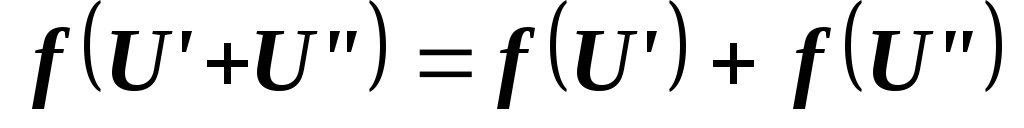 ,
если
,
если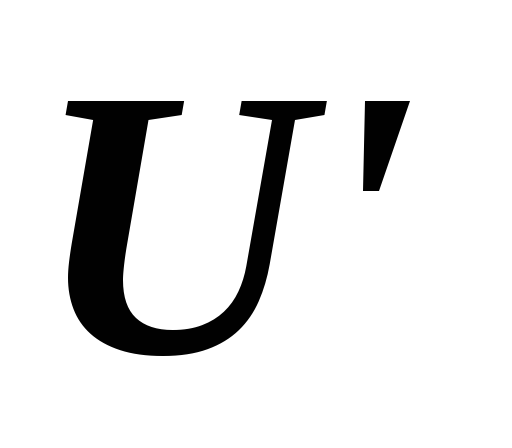 и
и –
подпространства линейного пространства
–
подпространства линейного пространства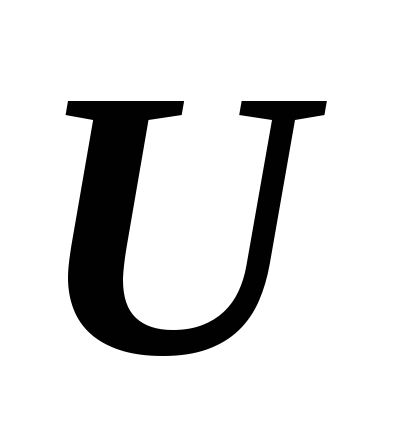 ?
?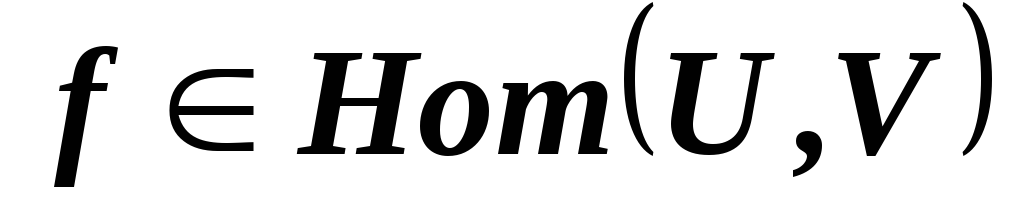 ,
верно ли, что
,
верно ли, что
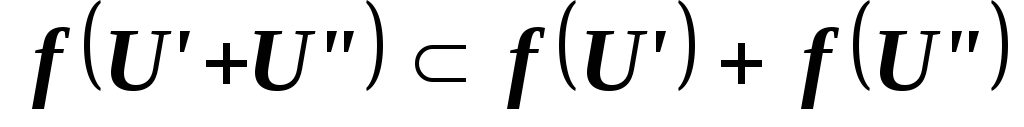 ,
если
,
если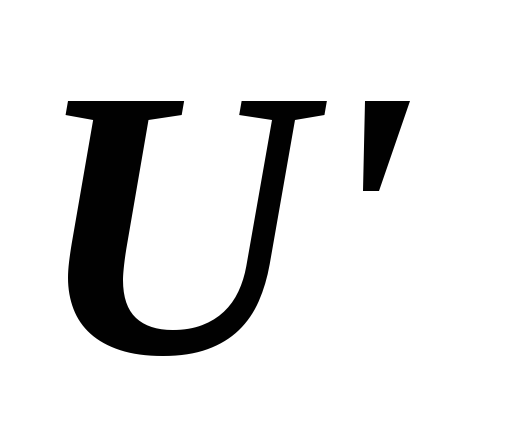 и
и –
подпространства линейного пространства
–
подпространства линейного пространства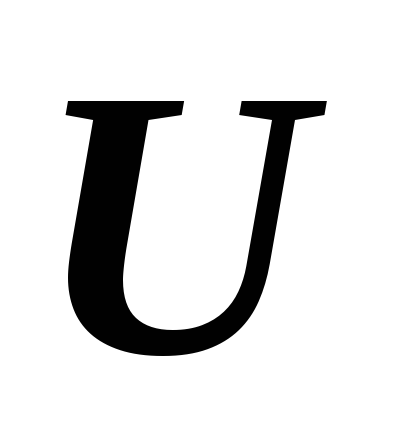 ?
? ,
верно ли, что
,
верно ли, что
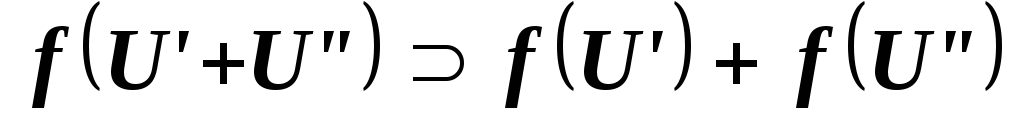 ,
если
,
если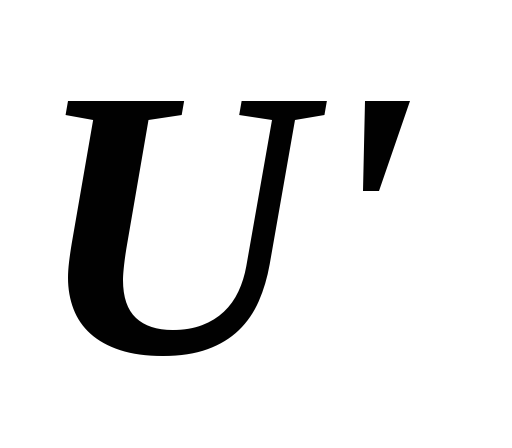 и
и –
подпространства линейного пространства
–
подпространства линейного пространства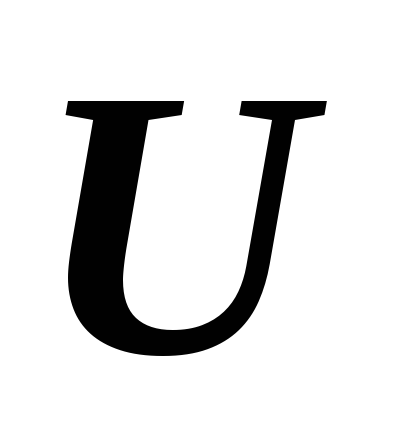 ?
?Для
 ортогонального
проектирования линейного пространства
всех свободных (геометрических) векторовV
ортогонального
проектирования линейного пространства
всех свободных (геометрических) векторовV на его одномерное подпространствоV
на его одномерное подпространствоV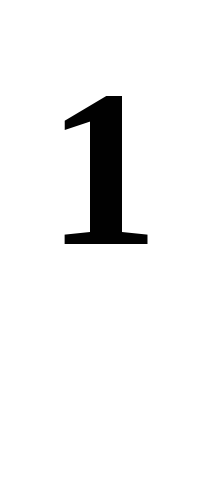 (свободных векторов, параллельных
некоторой прямой) укажите ядро и образ.
(свободных векторов, параллельных
некоторой прямой) укажите ядро и образ.Для
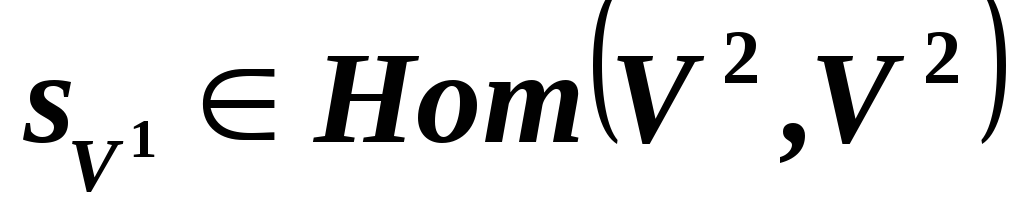 симметрии (отражения) линейного
пространства всех свободных
(геометрических) векторов относительно
его одномерного подпространстваV
симметрии (отражения) линейного
пространства всех свободных
(геометрических) векторов относительно
его одномерного подпространстваV (свободных векторов, параллельных
некоторой прямой) укажите ядро и образ.
(свободных векторов, параллельных
некоторой прямой) укажите ядро и образ.Докажите, что для любого
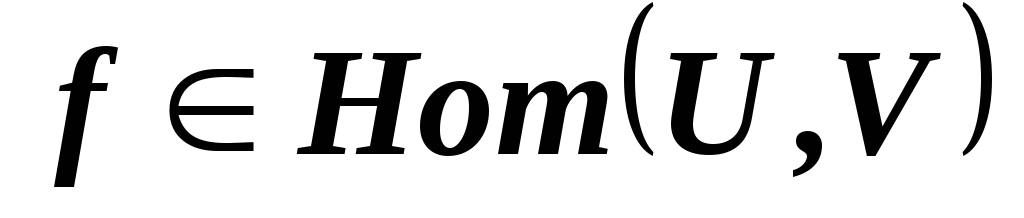 множество
множество является подпространством линейного
пространства
является подпространством линейного
пространства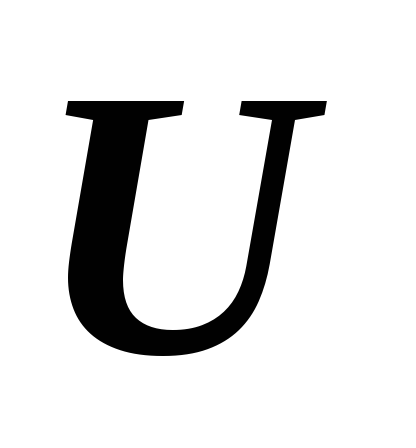 .
.Докажите, что для любого
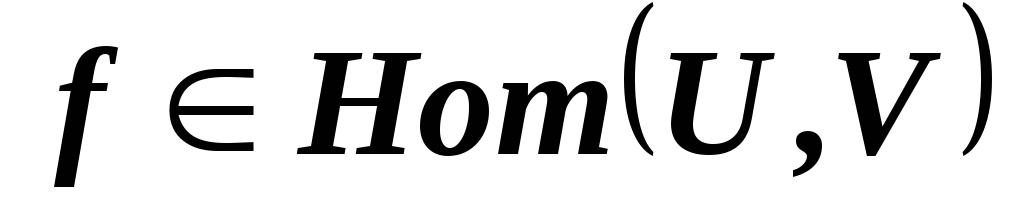 множество
множество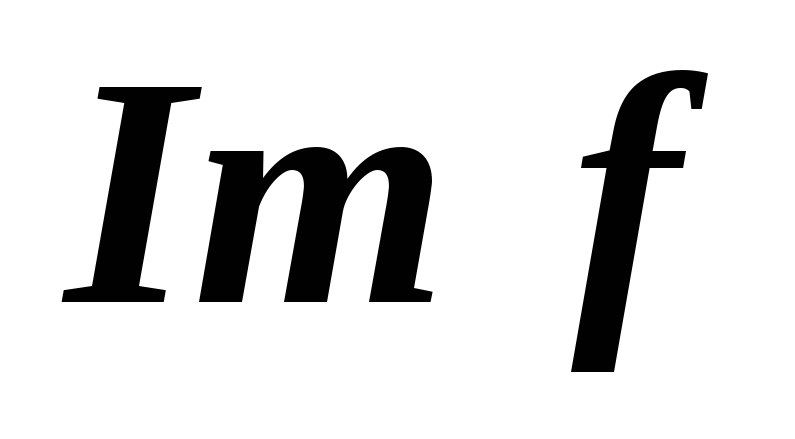 является подпространством линейного
пространства
является подпространством линейного
пространства .
.Докажите, что отображение
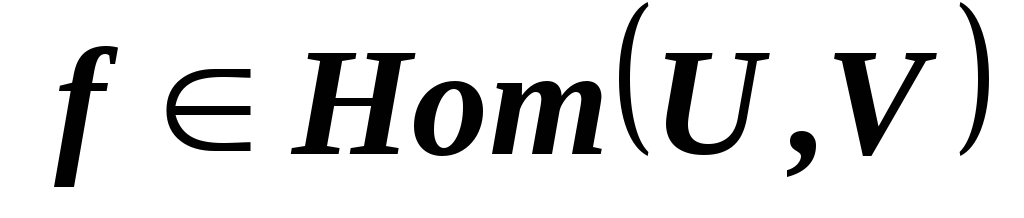 ,
, инъективно тогда и только тогда, когда
инъективно тогда и только тогда, когда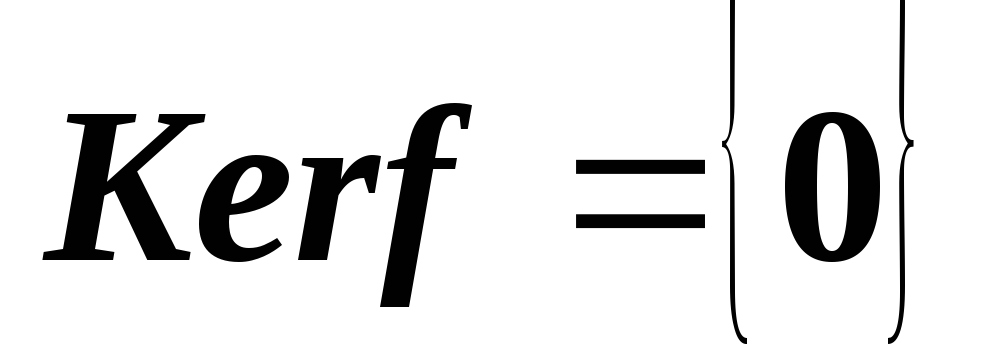 .
..
 и имеет нулевое ядро. Означает ли это,
что сюръективность
и имеет нулевое ядро. Означает ли это,
что сюръективность ?
?Докажите, что отображение
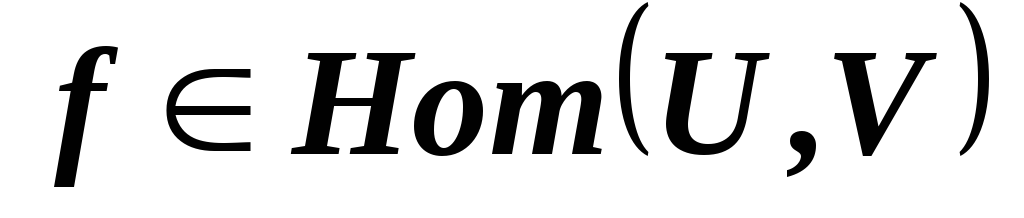 есть изоморфизм линейных пространства
тогда и только тогда, когда
есть изоморфизм линейных пространства
тогда и только тогда, когда ,
а
,
а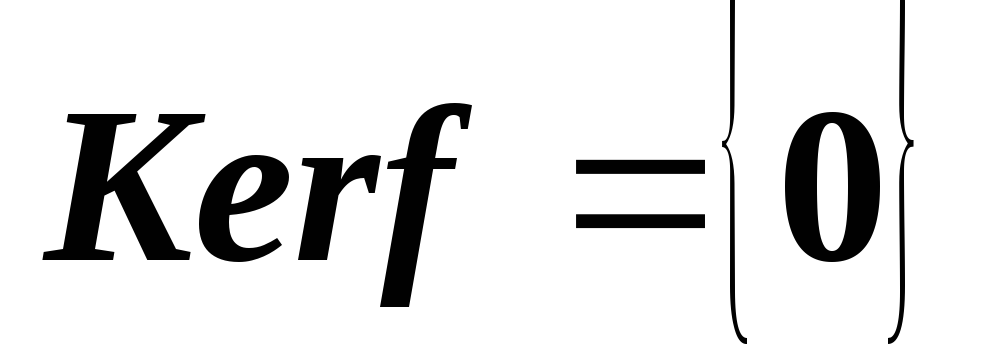 .
.*Как связаны ранг и дефект линейного отображения и свойство сюръективности этого отображения?
*Как связаны ранг и дефект линейного отображения и свойство инъективности этого отображения?
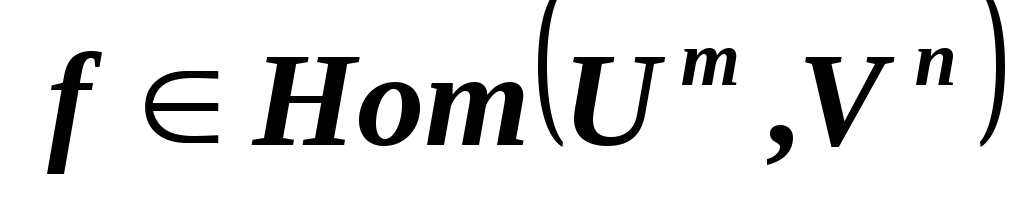 ,
сравните размерности:
,
сравните размерности:
 с размерностями пространств
с размерностями пространств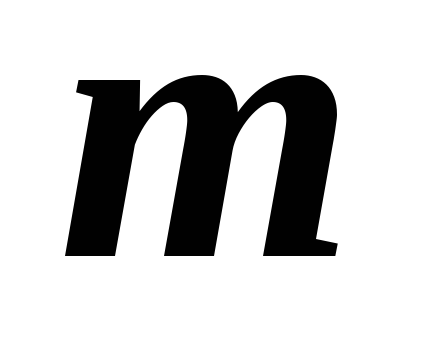 и
и .
.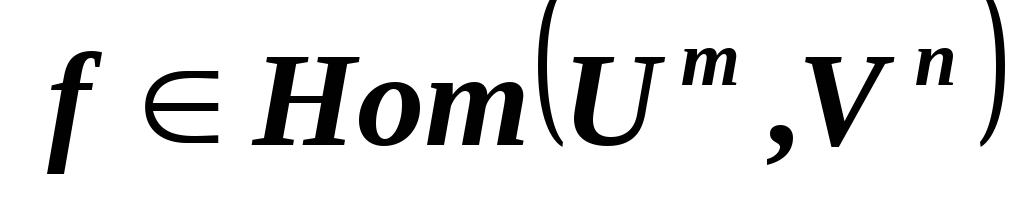 ,
сравните размерности:
,
сравните размерности:
 с размерностями пространств
с размерностями пространств и
и .
.*
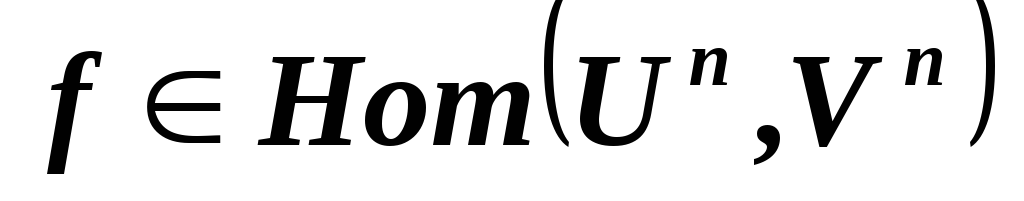 и является изоморфизмом этих линейных
пространств, укажите
и является изоморфизмом этих линейных
пространств, укажите
 и
и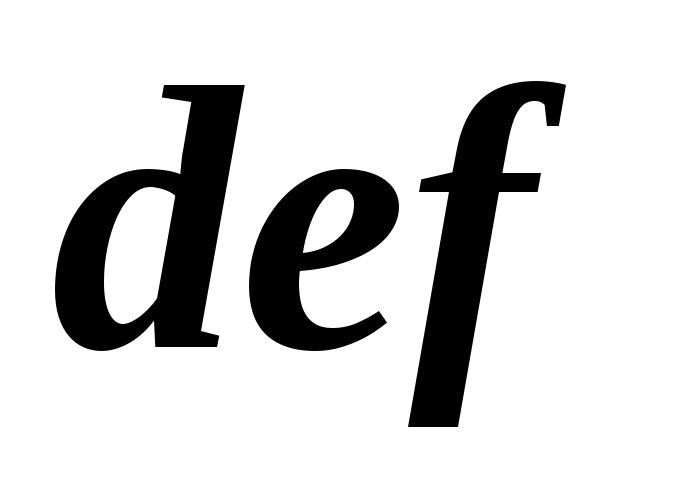
 .
.*Определите условия, когда
 имеет обратное отображение.
имеет обратное отображение.*Докажите, что для
 существует обратное отображение, причем
существует обратное отображение, причем
*Докажите, что свойство линейных пространств «быть изоморфными» есть отношение эквивалентности на множестве всех линейных пространств.
Известно, что ранг матрицы
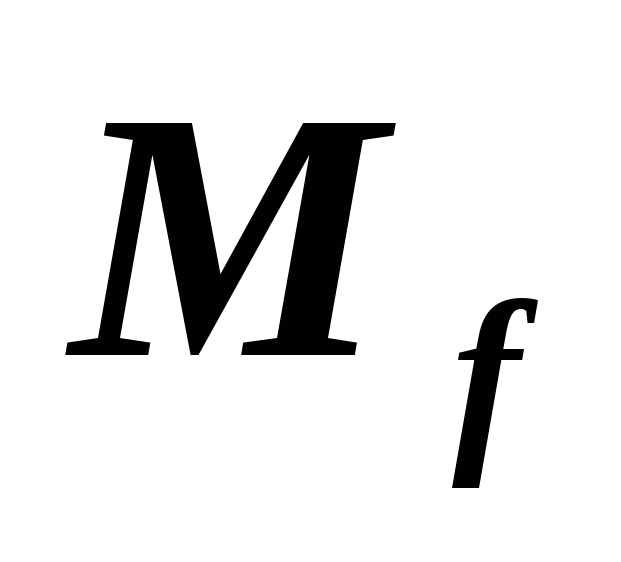 линейного отображения
линейного отображения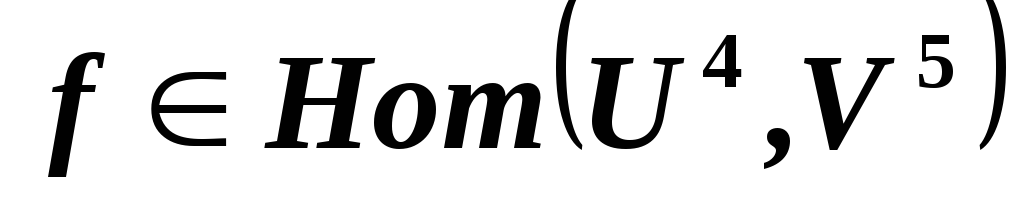 равен 3. Можно ли определить размерность
ядра этого отображения?
равен 3. Можно ли определить размерность
ядра этого отображения?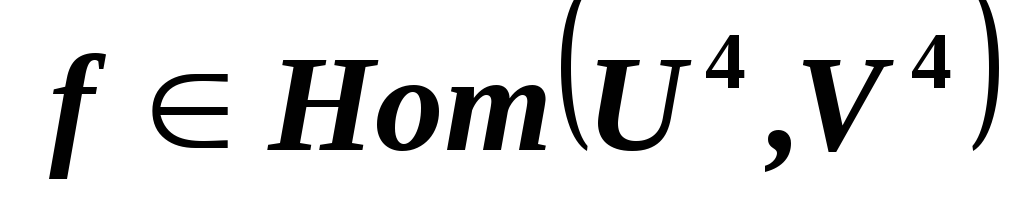 и имеет нулевое
ядро. Следует ли из этого, что отображение
и имеет нулевое
ядро. Следует ли из этого, что отображение
 является изоморфизмом этих пространств?
является изоморфизмом этих пространств?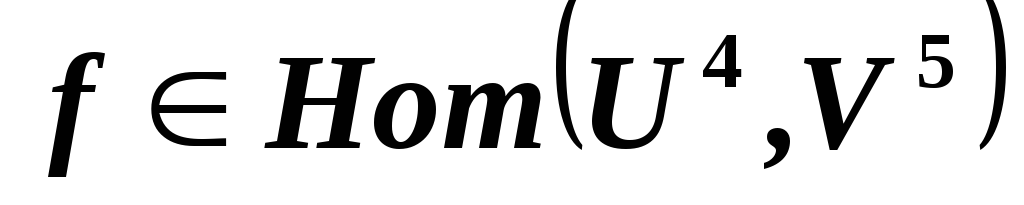 и имеет нулевое
ядро. Является ли отображение
и имеет нулевое
ядро. Является ли отображение
 сюръективным?
сюръективным?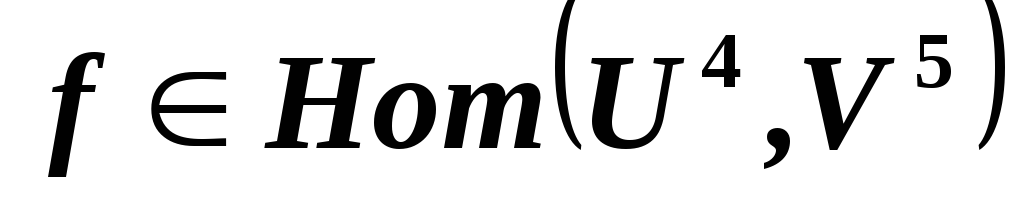 и
и
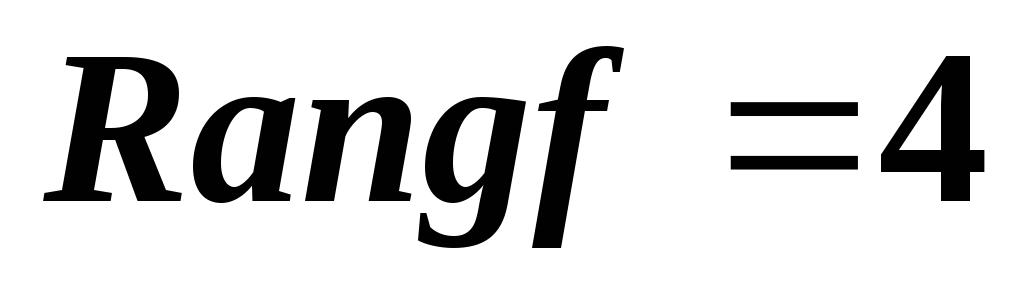 .
Является ли отображение
.
Является ли отображение инъективным?
инъективным?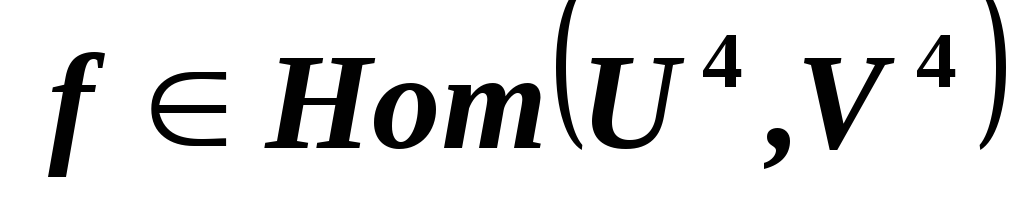 и
и
 .
Означает ли это инъективность отображения
.
Означает ли это инъективность отображения ?
?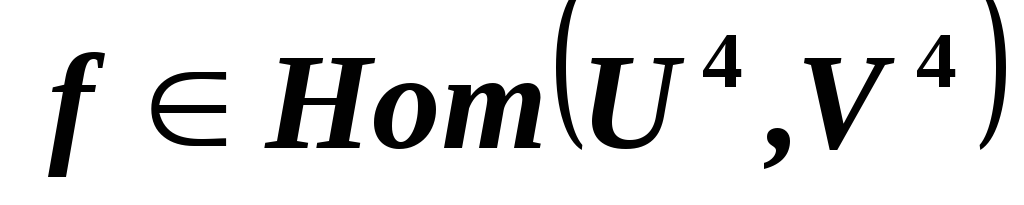 и
и
 .
Следует ли из этого, что отображение
.
Следует ли из этого, что отображение является изоморфизмом этих пространств?
является изоморфизмом этих пространств?Может ли матрица
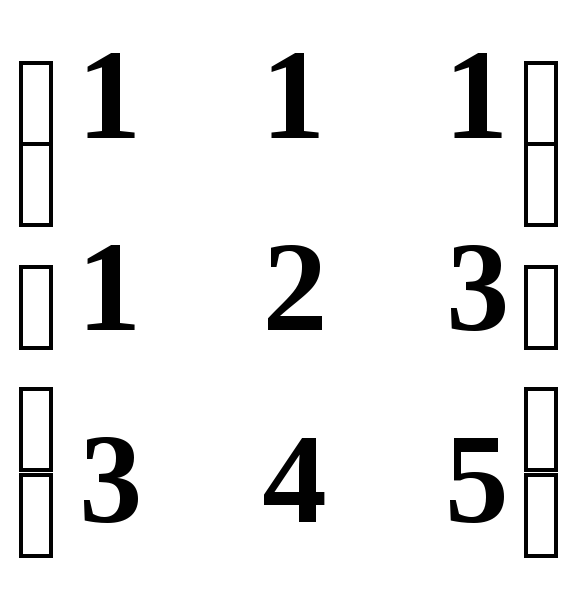 быть матрицей изоморфизма каких-либо
линейных пространств?
быть матрицей изоморфизма каких-либо
линейных пространств?Может ли матрица
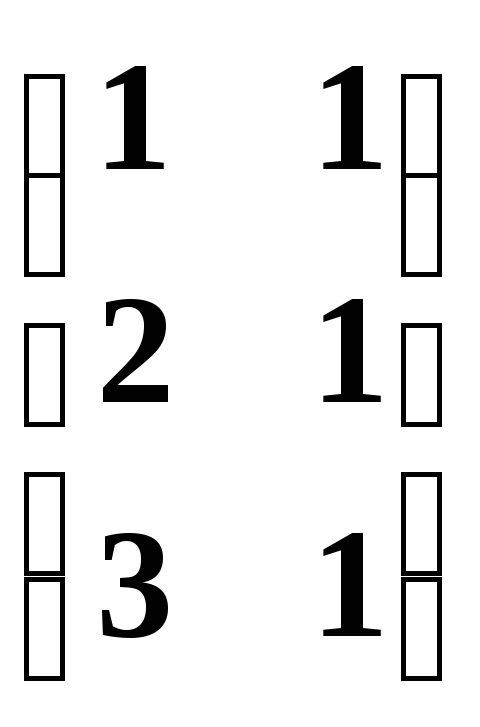 быть матрицей изоморфизма каких-либо
линейных пространств?
быть матрицей изоморфизма каких-либо
линейных пространств?Может ли матрица
 быть матрицей изоморфизма каких-либо
линейных пространств?
быть матрицей изоморфизма каких-либо
линейных пространств?Докажите, что если
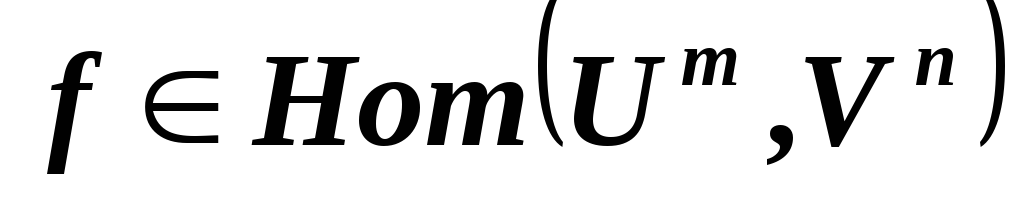 ненулевое отображение, то существуют
базисы
ненулевое отображение, то существуют
базисы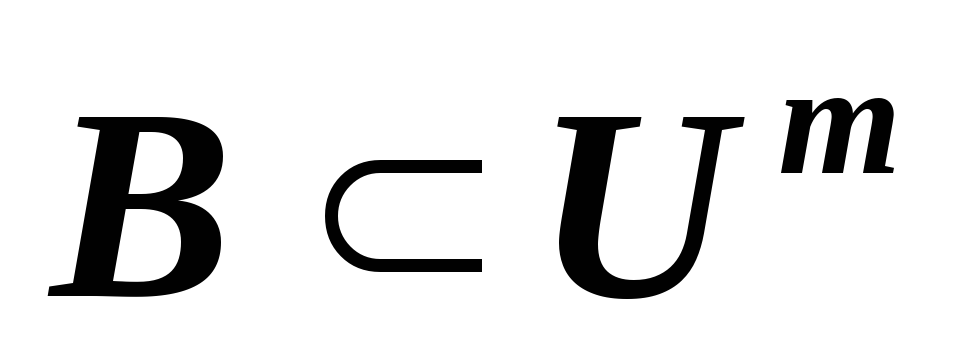 и
и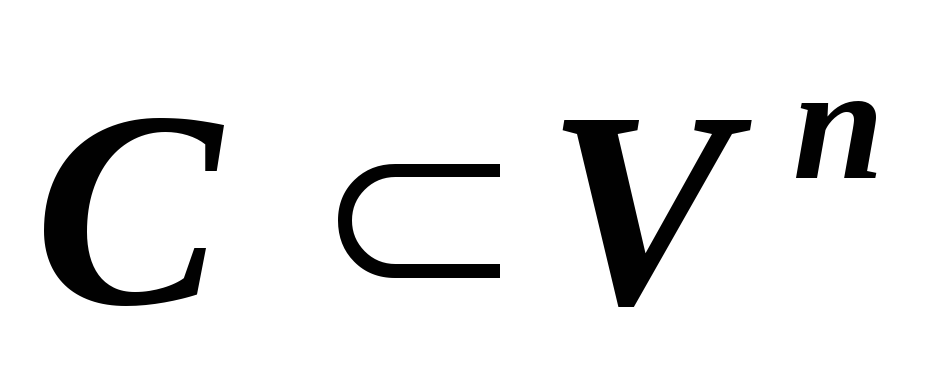 ,
относительно которых матрица
,
относительно которых матрица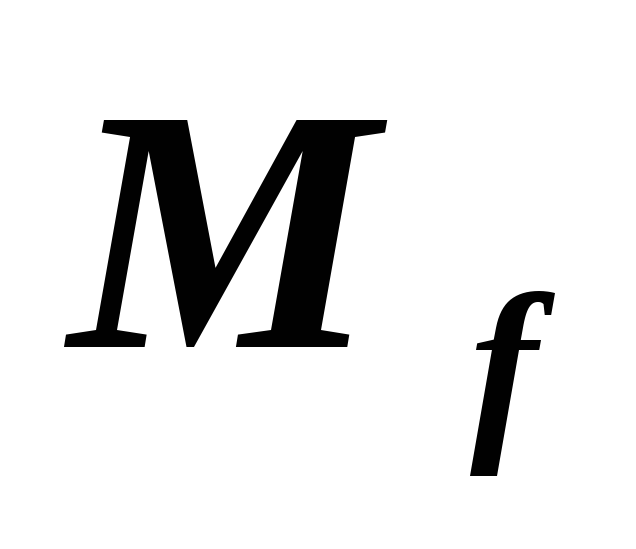 имеет вид
имеет вид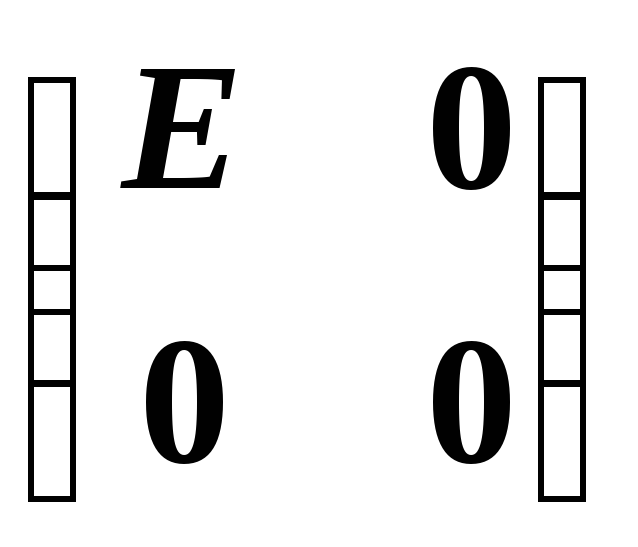 ,
где
,
где –
единичная матрица порядка не выше
–
единичная матрица порядка не выше .
.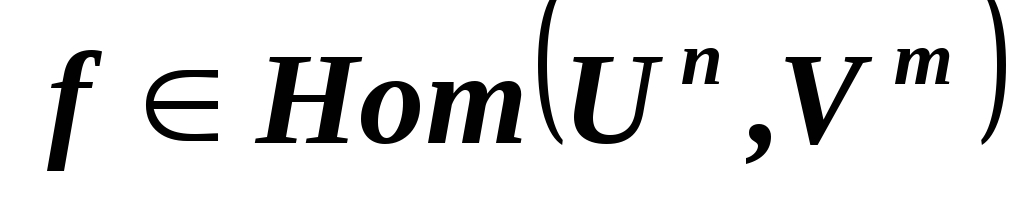 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма
 относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах и, соответственно,
и, соответственно,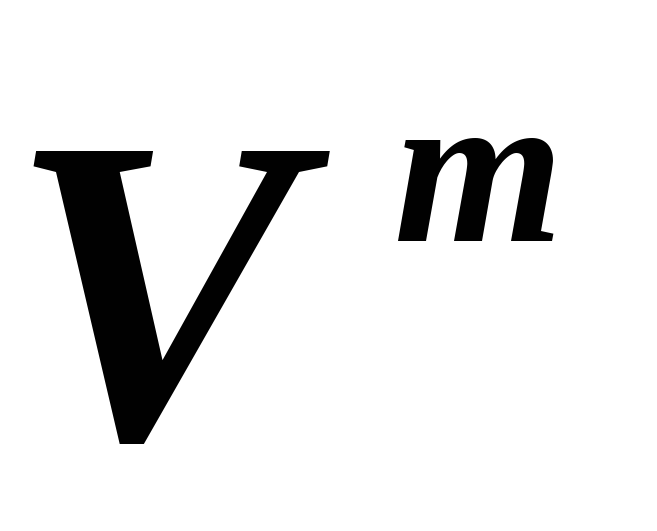 ,
если в базисе
,
если в базисе поменять местами первый и второй
векторы?
поменять местами первый и второй
векторы?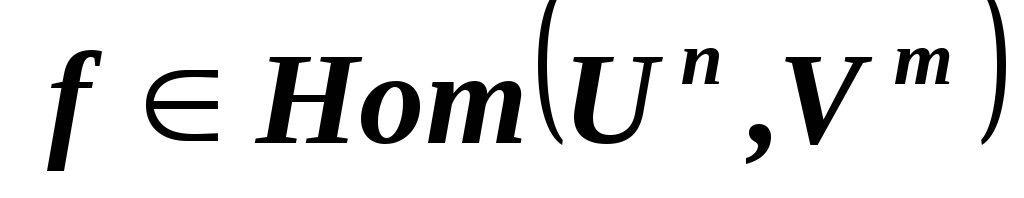 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма
 относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах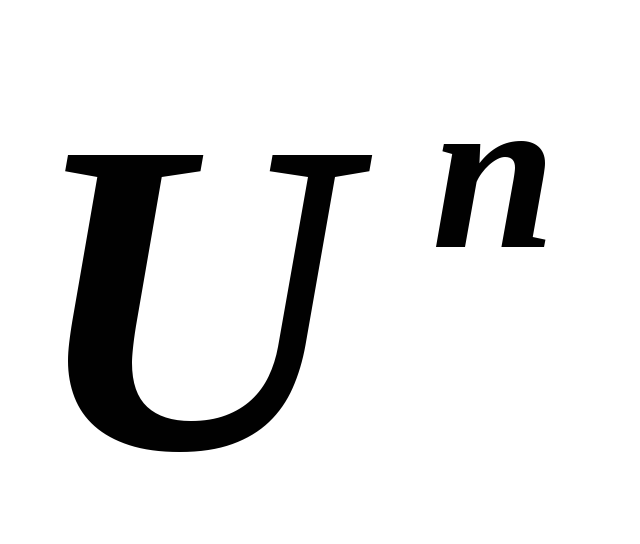 и, соответственно,
и, соответственно,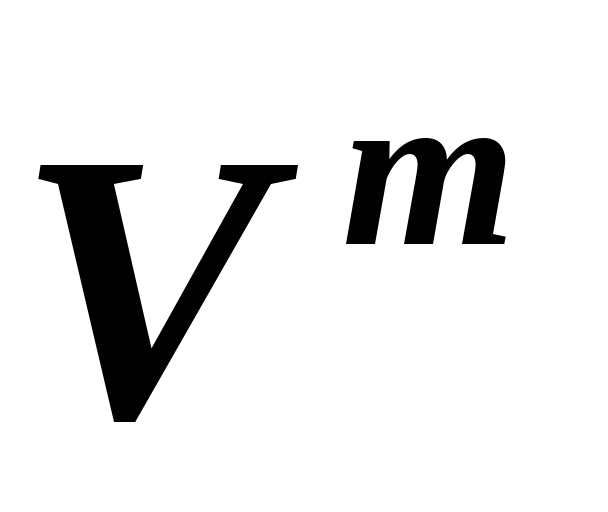 ,
если в базисе
,
если в базисе изменить порядок векторов на
противоположный?
изменить порядок векторов на
противоположный?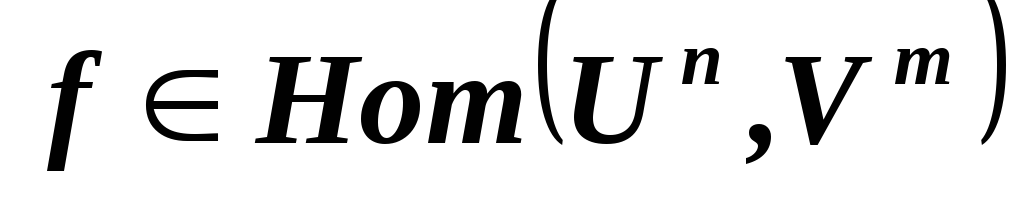 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма
 относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах и, соответственно,
и, соответственно,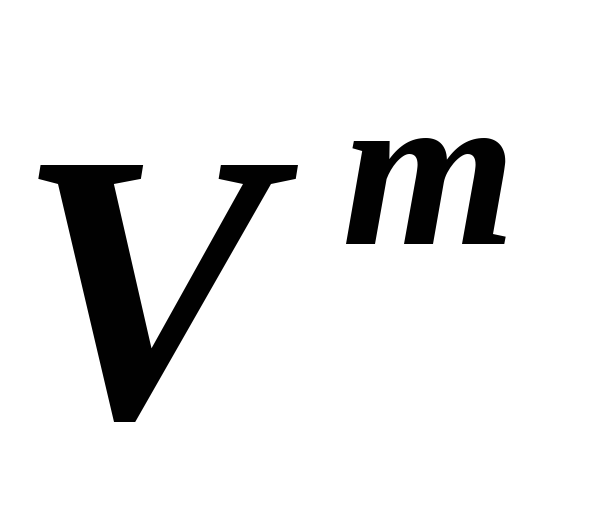 ,
если в базисе
,
если в базисе поменять местами первый и второй
векторы?
поменять местами первый и второй
векторы?*
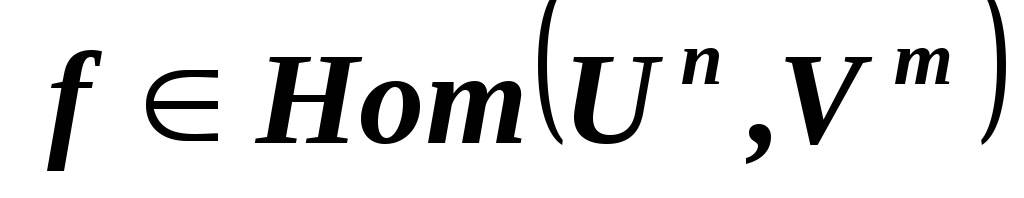 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах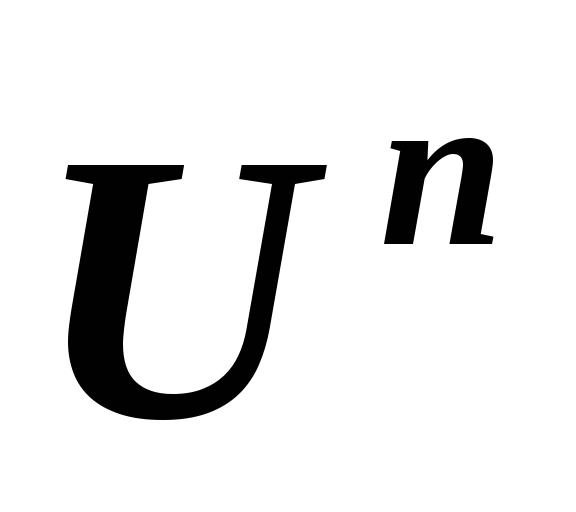 и, соответственно,
и, соответственно,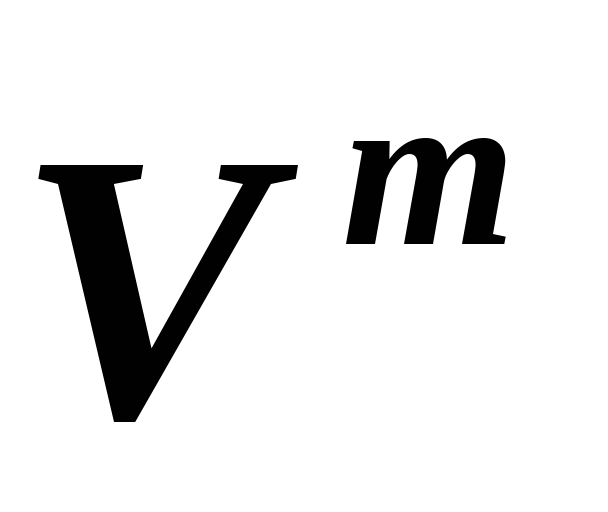 ,
если в каждом из базисов поменять
местами первые и вторые векторы?
,
если в каждом из базисов поменять
местами первые и вторые векторы?*
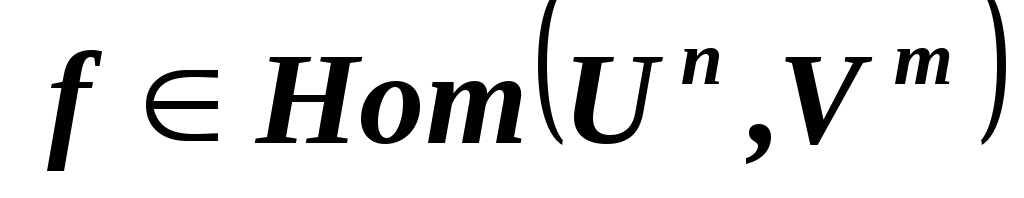 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах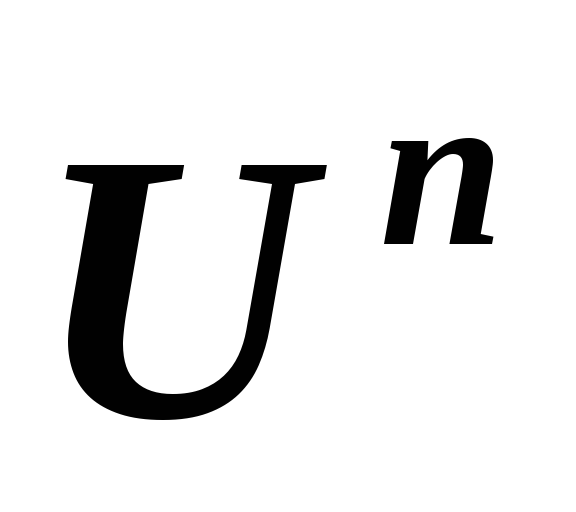 и, соответственно,
и, соответственно,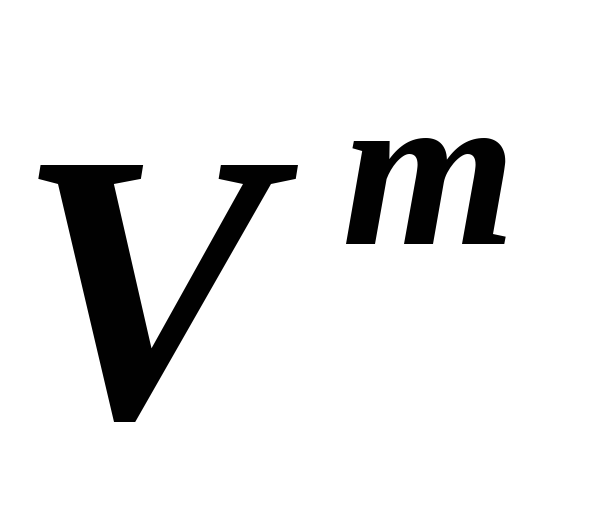 ,
если в базисе
,
если в базисе изменить порядок его векторов на
противоположный?
изменить порядок его векторов на
противоположный?*
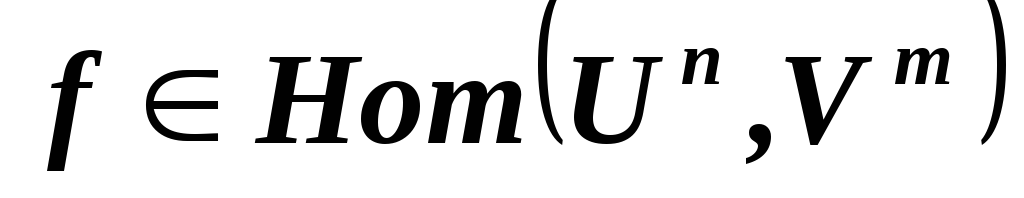 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах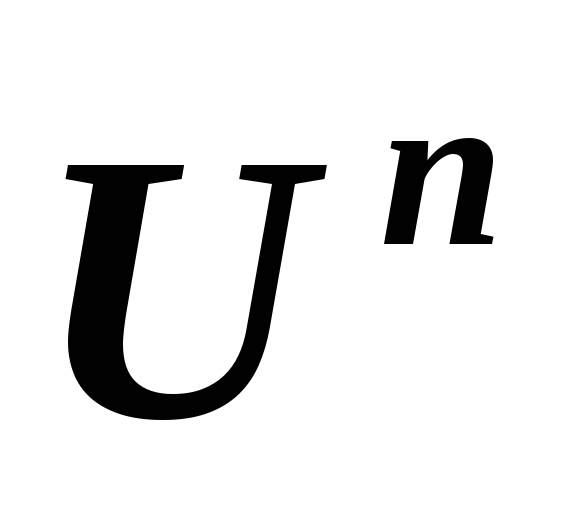 и, соответственно,
и, соответственно,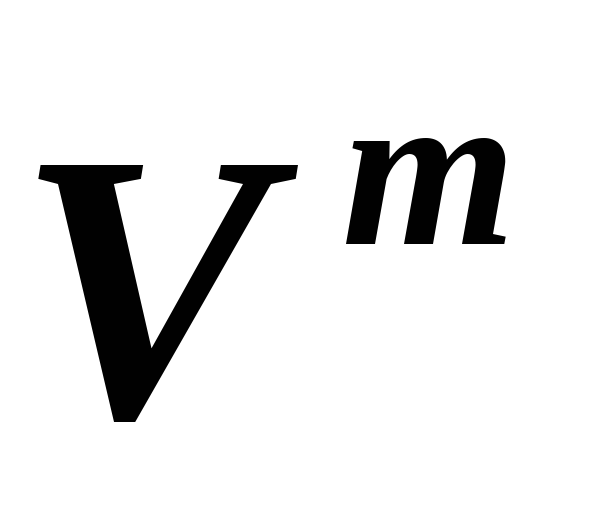 ,
если в каждом из базисов
,
если в каждом из базисов и
и изменить порядок его векторов на
противоположный?
изменить порядок его векторов на
противоположный?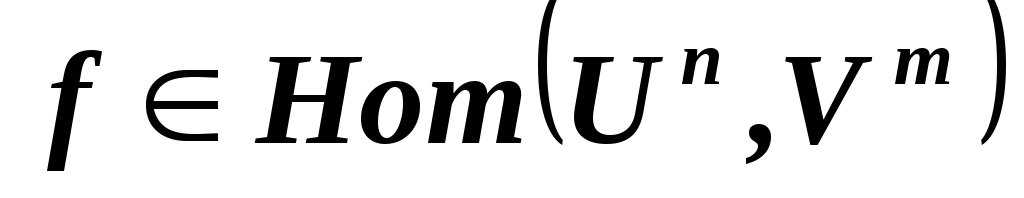 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма
 относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах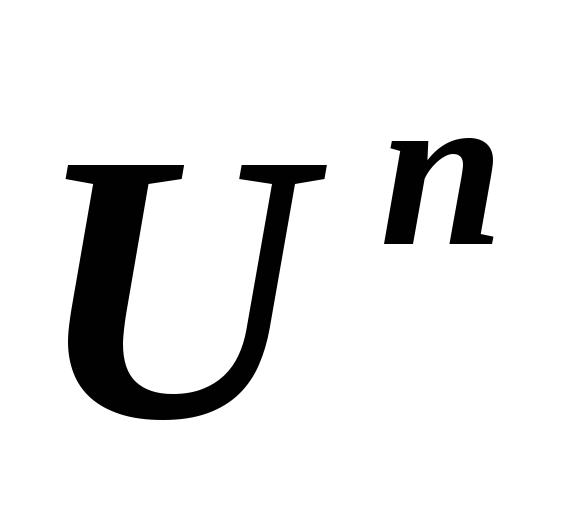 и, соответственно,
и, соответственно,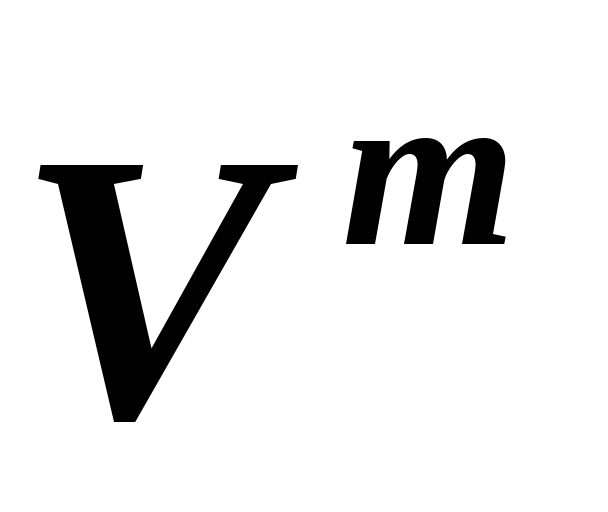 ,
если в базисе
,
если в базисе первый вектор умножить на 2?
первый вектор умножить на 2? ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма
 относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах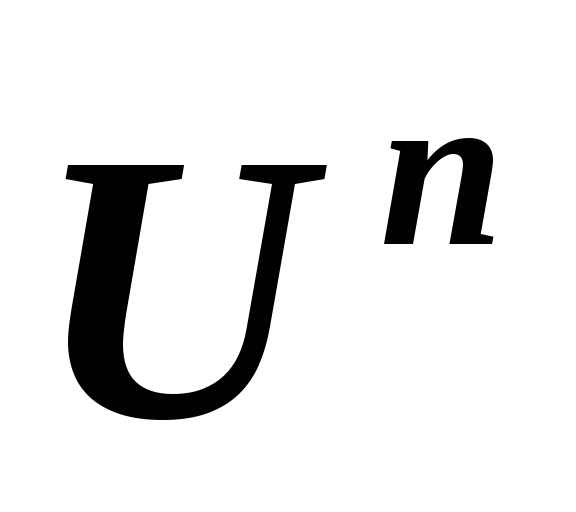 и, соответственно,
и, соответственно, ,
если в базисе
,
если в базисе первый вектор умножить на 2?
первый вектор умножить на 2?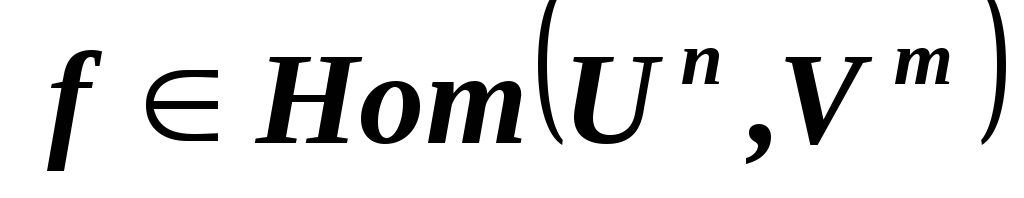 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма
 относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах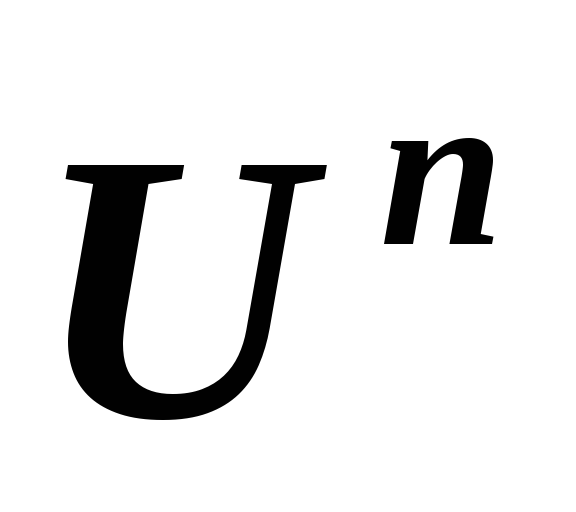 и, соответственно,
и, соответственно,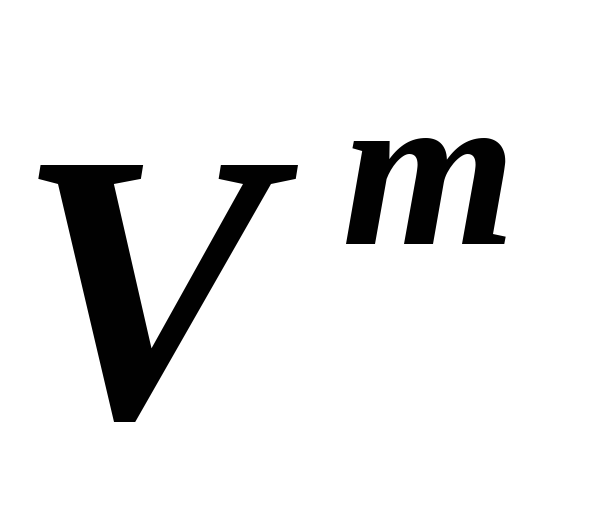 ,
если в каждом из базисов первые векторы
умножить на 2?
,
если в каждом из базисов первые векторы
умножить на 2?*
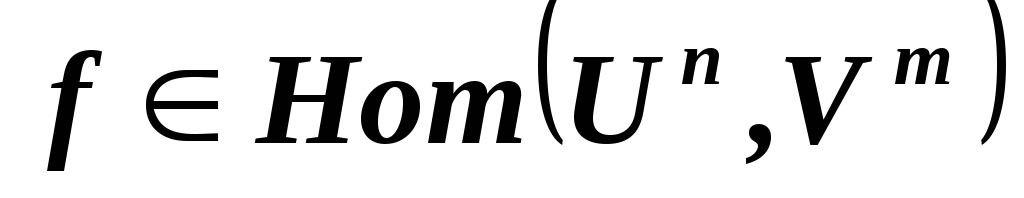 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах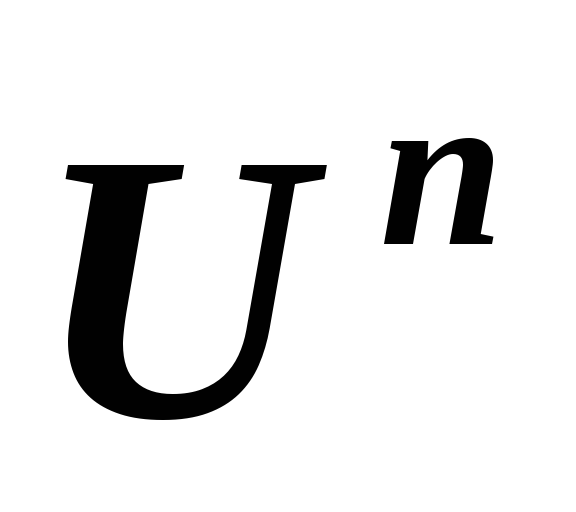 и, соответственно,
и, соответственно, ,
если все векторы базисов
,
если все векторы базисов и
и умножить на 2?
умножить на 2?*
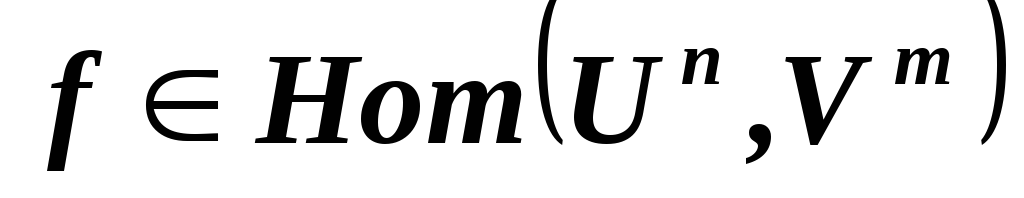 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах и, соответственно,
и, соответственно,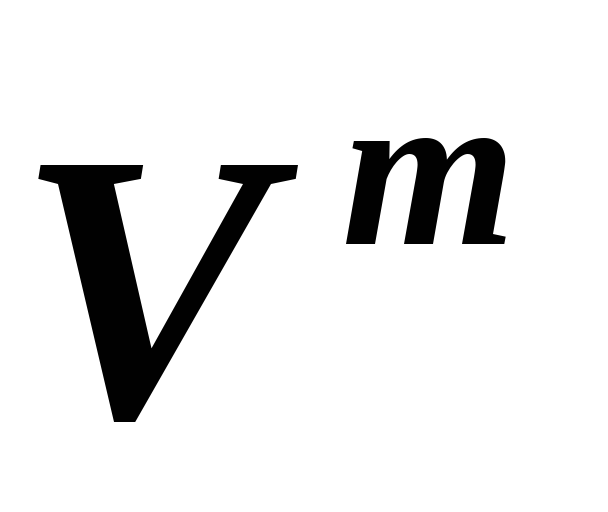 ,
если все векторы базиса
,
если все векторы базиса умножить на 2, а все векторы базиса
умножить на 2, а все векторы базиса поделить на 2?
поделить на 2?*
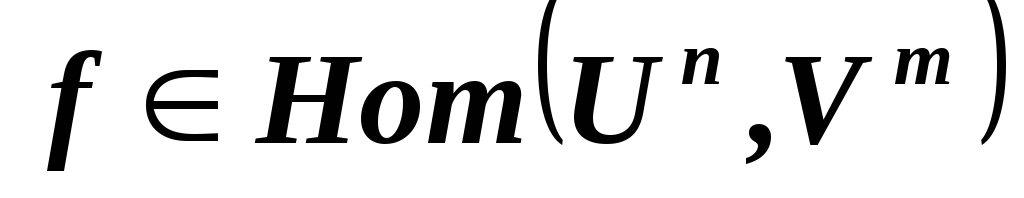 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах и, соответственно,
и, соответственно,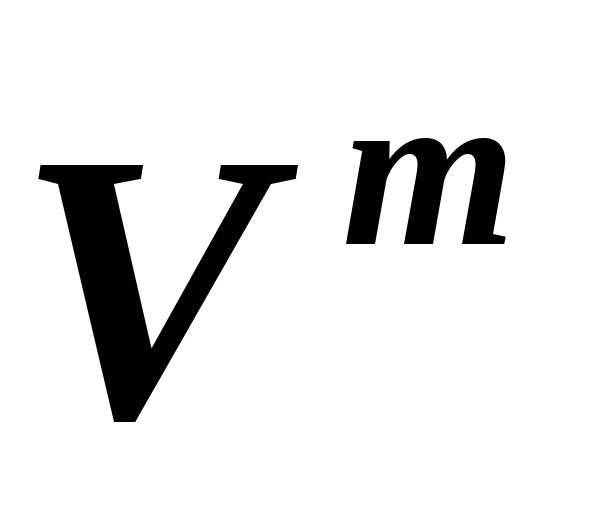 ,
если все векторы базиса
,
если все векторы базиса умножить на 2, а все векторы базиса
умножить на 2, а все векторы базиса умножить на 4?
умножить на 4?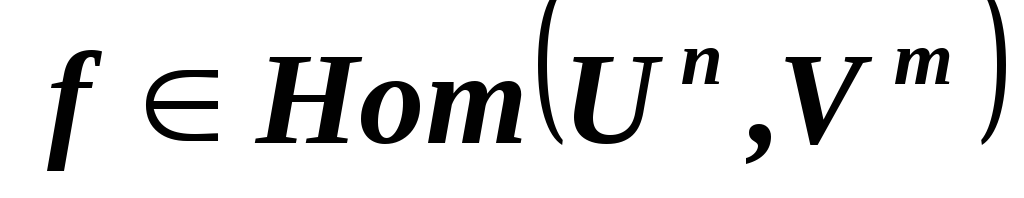 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма
 относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах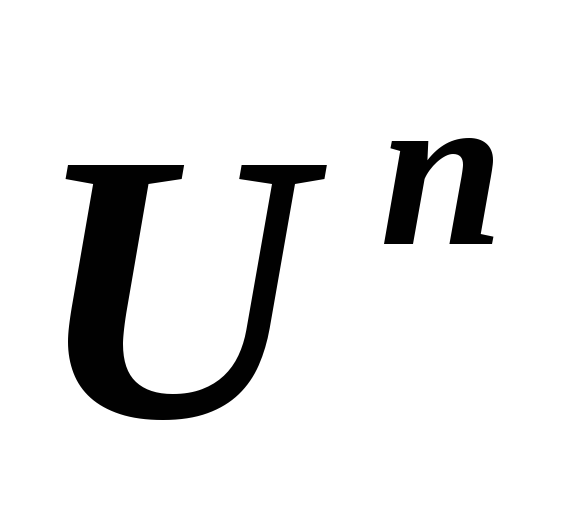 и, соответственно,
и, соответственно,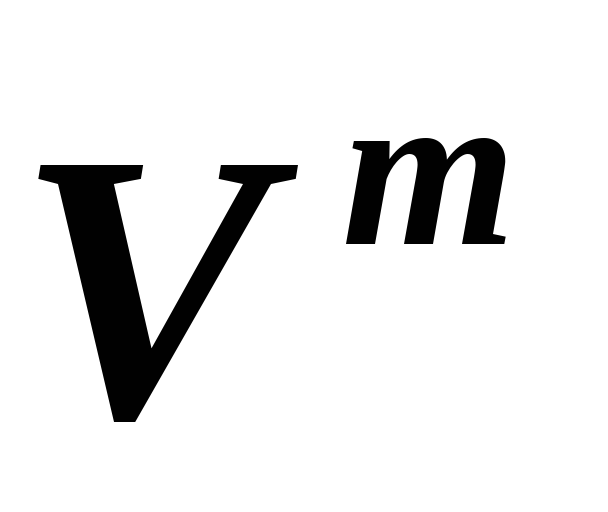 ,
если в базисе
,
если в базисе к первому базисному вектору прибавить
второй базисный вектор?
к первому базисному вектору прибавить
второй базисный вектор?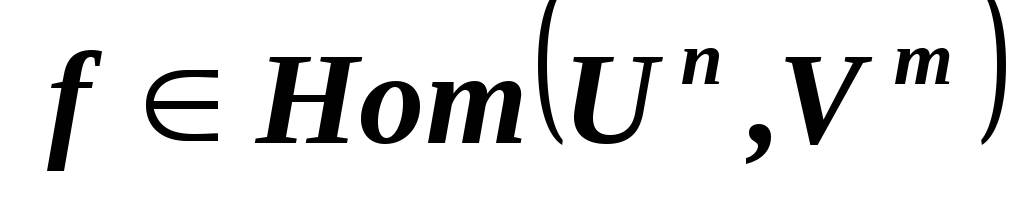 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма
 относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах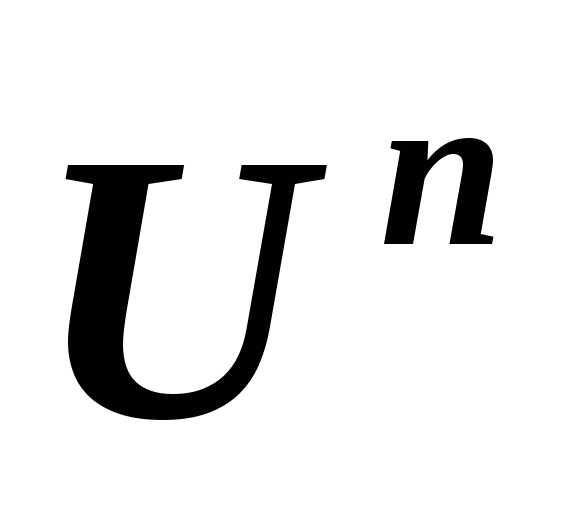 и, соответственно,
и, соответственно, ,
если в базисе
,
если в базисе к первому базисному вектору прибавить
второй базисный вектор?
к первому базисному вектору прибавить
второй базисный вектор?*
 ,
как изменится матрица гомоморфизма
,
как изменится матрица гомоморфизма относительно базисов
относительно базисов и
и в линейных пространствах
в линейных пространствах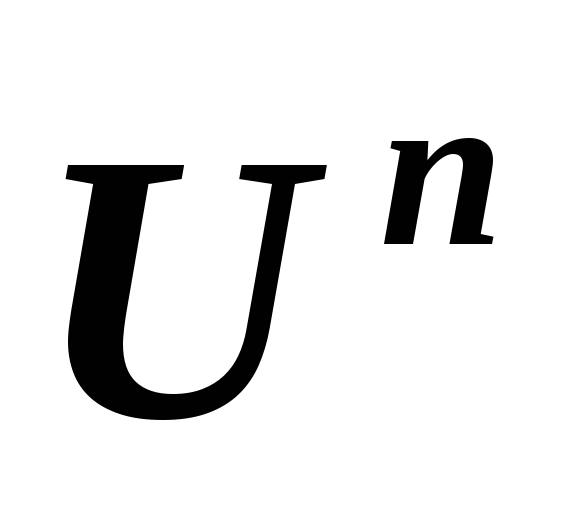 и, соответственно,
и, соответственно,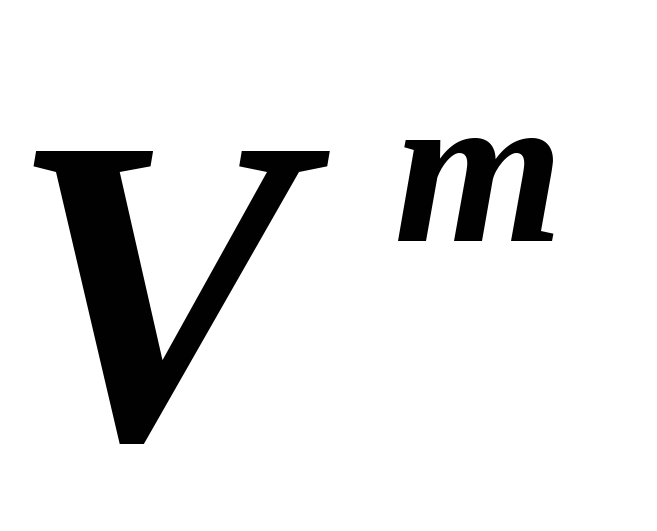 ,
если в каждом из базисов
,
если в каждом из базисов и
и к первому базисному вектору прибавить
второй базисный вектор этого базиса?
к первому базисному вектору прибавить
второй базисный вектор этого базиса?Докажите, что
 ⊞
⊞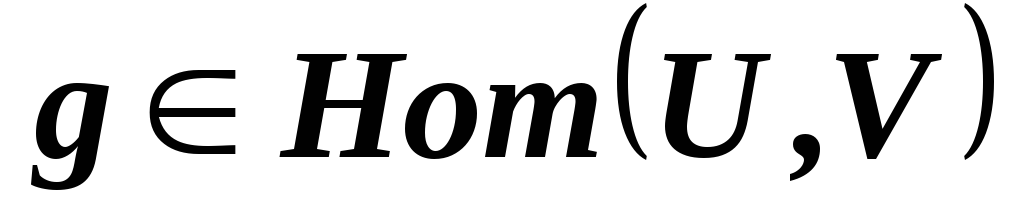 ,
если отображения
,
если отображения ,
а
,
а ⊞
⊞ –
их сумма, т.е.
–
их сумма, т.е.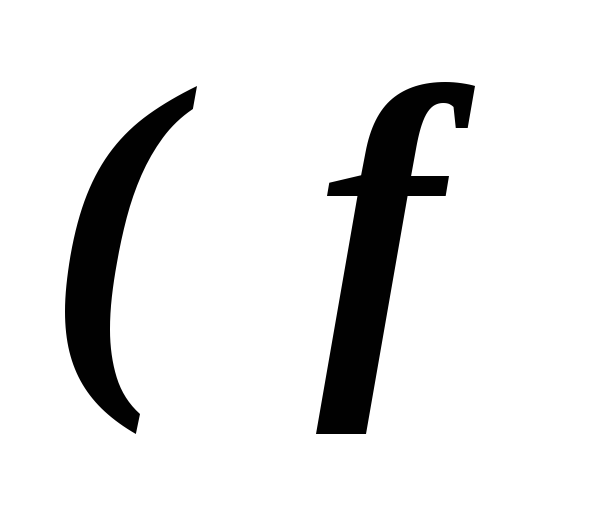 ⊞
⊞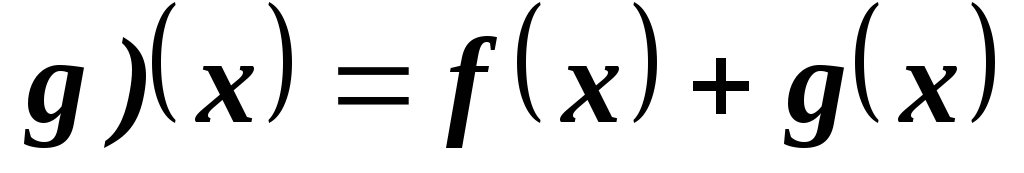 для любого
для любого .
.Докажите, что если отображение
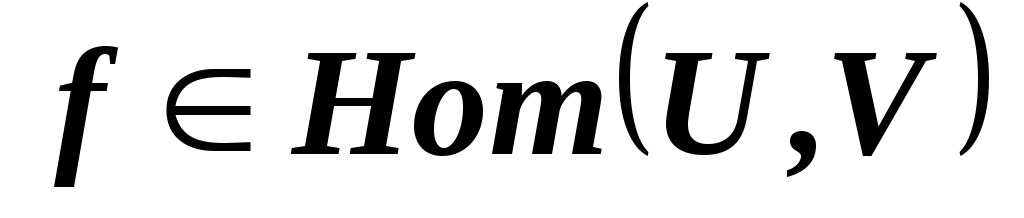 ,
то
,
то ⊡
⊡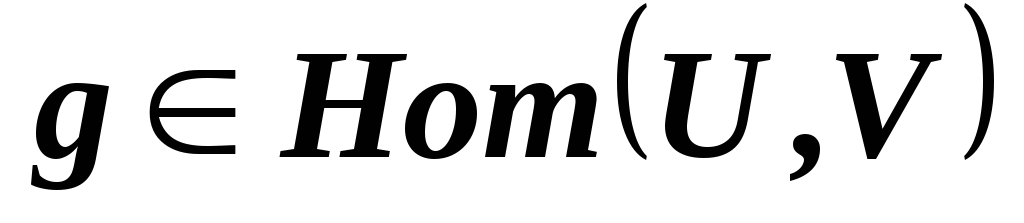 при любом
при любом ,
где
,
где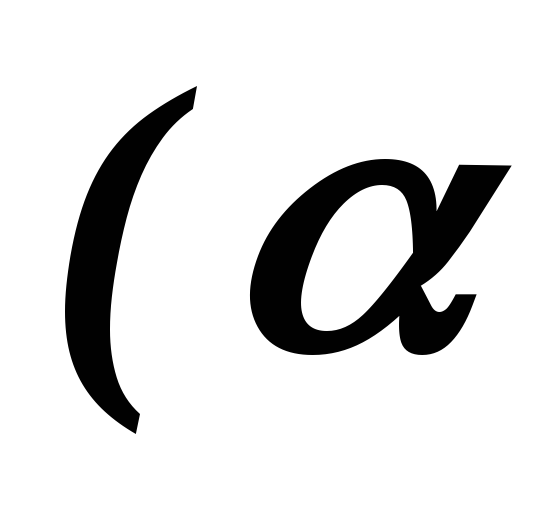 ⊡
⊡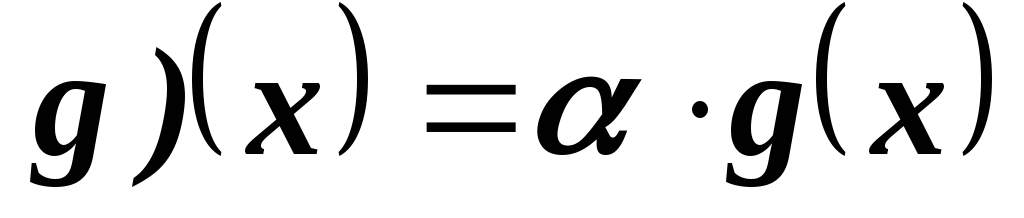 для любого
для любого .
.*Докажите, что
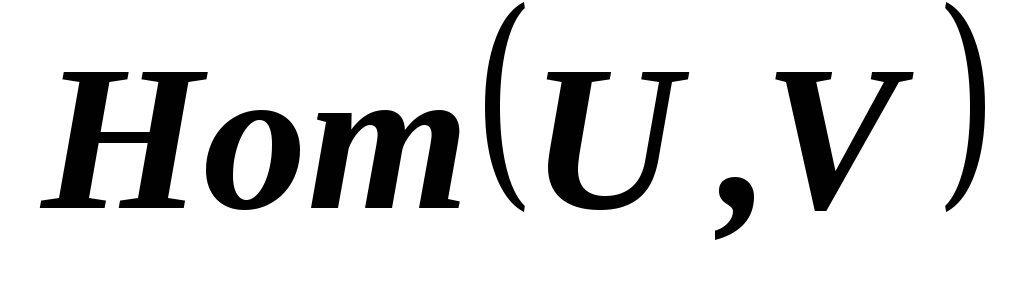 является линейным пространством
относительно естественных операций
сложения и гомоморфизмов и умножения
их на число (см. задачи 218 и 217).
является линейным пространством
относительно естественных операций
сложения и гомоморфизмов и умножения
их на число (см. задачи 218 и 217).
