2.7.Байесовская форма игры
Игра с неполной информацией – это игра, в которой в первый момент времени, когда игроки еще только начинают планировать свои движения в игре, некоторые игроки уже имеют частную информацию, которой не обладают другие игроки. Первоначальная частная информация, которую игрок имеет до этого момента времени, называется типом игрока.
Harsanyi(1967-1968) предложил стратегическую форму игры с неполной информацией и назвал ее Байесовской формой игры:
.
Игра конечна, если N,
конечные
множества.
Обозначения:
,
,
то есть
обозначает субъективную вероятность того, чтоt-i- это действительно набор типов других игроков (по мнению игрока i, имеющего собственный типti)
.
Сi– множество действий. Стратегия игрока i в Гв– это функция из множества типов Тiв множество действийCi
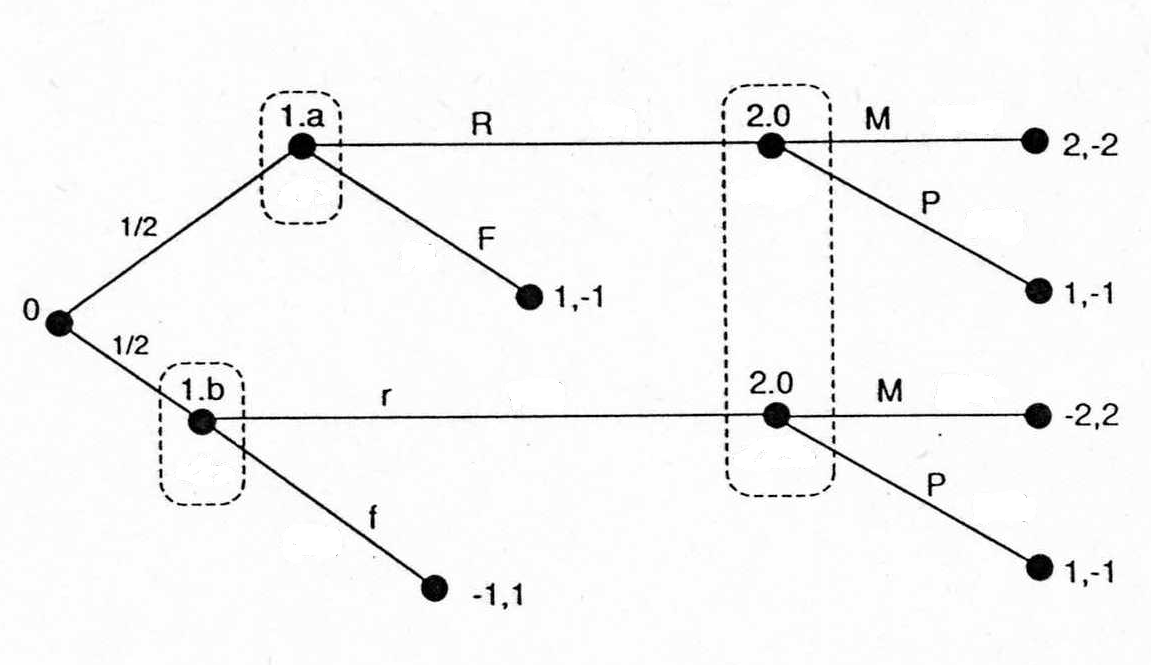
Простая карточная игра стала бы игрой с неполной информацией, если бы предположили, что игрок 1 уже знал, какого цвета его карта, до того момента, когда игра началась. Тогда бы представление этой игры в форме Байеса было бы такое:
N={1,2},T1={1.a,1.b},T2={2.0},C1={R,F},S={M,P},
p2(1.a|2)=0,5=p2(1.b|2), т.к. 2-й игрок думает, что красная и черная карта одинаково вероятны.
p1(2|1.a)=1=p1(2|1.b), т.к. 1-й игрок знает тип 2-го игрока
Функции полезности u1(c,t),u2(c,t) зависят от (c,t)=(c1,c2,t)
|
t1=1.a |
M |
P |
|
t1=1.b |
M |
P |
|
R |
2,-2 |
1,-1 |
R |
-2,2 |
1,-1 | |
|
F |
1,-1 |
1,-1 |
F |
-1,1 |
-1,1 |
Пример – простейший аукцион
1-й игрок продает товар, 2-й покупает. Каждый игрок знает, сколько стоит объект для него самого, но думает, что цена объекта для другого игрока может быть с вероятностью 1/100 любым числом от 1 до 100. В игре каждый игрок одновременно предлагает цену от 0 до 100 за продажу объекта. Если цена покупателя больше или равна цене продавца, тогда товар продается по цене, равной средней величине их цен. В противном случае – не продается. Функция полезности равна выручке от продажи.
Представление аукциона в виде игры Байеса:
Множество игроков N={1,2}, множество типов Тi={1,2,…,100}. Тип совпадает с ценой объекта для игрока. Множество действий (название цены) Сi={1,2,…,100}. Функции вероятности такие:
pi(t-i|ti)=1/100,
.
Функции полезности:
u1(c,t)=(c1+c2)/2 –t1,c2≥c1,
u2(c,t)=t2-(c1+c2)/2, c2≥c1,
u1(c,t)=0= u2(c,t), c2<c1.
2.8.Совместимость мнений
Мы говорим, что мнения (pi)iєNв игре Байеса совместны тогда и только тогда, когда существует распределение P(t),tєT, такое, что
,
,
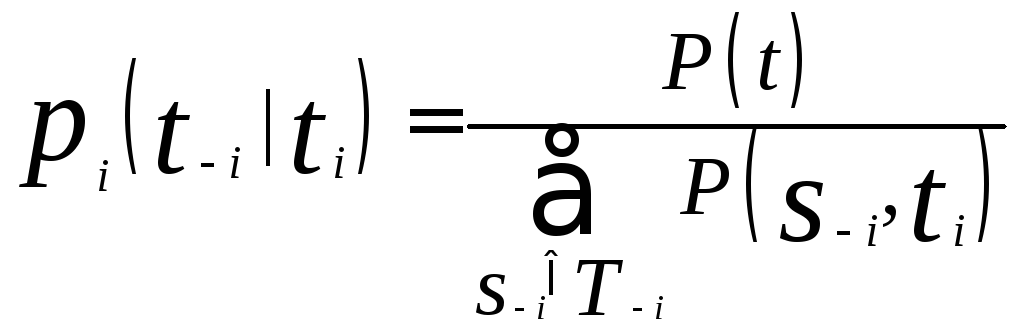где i-я компонента –ti, а все остальные компоненты как вs-i.
Задав одну функцию можно подсчитать вероятностные распределения, характеризующие мнения всех игроков, всех типов.
В простой карточной игре с предварительным распределением P(1.a,2.0)=P(1.b,2.0)=0,5.
Почему?
T={(1.a,2.0), (1.b,2.0)},
p2(1.a|2.0)=P(1.a,2.0)/(P(1.a,2.0)+P(1.b,2.0))=0,5/(0,5+0,5)=0,5,
p1(2.0|1.а)=P(1.a,2.0)/P(1.a,2.0)=1,
p2(2.0|1.b)=1
Мнения в конечной игре продавец-покупатель согласованы с предварительным
распределением P(t)=1/10000,
.
Почему?
,
.