4.9.Прямая индукция
Последовательная рациональность – это принцип, при применении которого для анализа игр в развернутой форме используется обратная индукция.
Сначала предсказывается поведение игроков в конце игры. Эти предсказания используются игроками на более ранних стадиях игры.
В 1986г. KohlbergиMertensвысказали предположение, что для анализа
игр
можно
использовать прямую индукцию. Принцип
прямой индукции значил бы, что поведение
рациональных разумных игроков в подыгре
может зависеть от выборов, которые были
у них в распоряжении на более ранних
стадиях игры.
В этой игре три сценария последовательного
равновесия:
,
и
.
Но доводы прямой индукции могут уничтожить
первые два из них. Второй игрок будет
при этом рассуждать так:
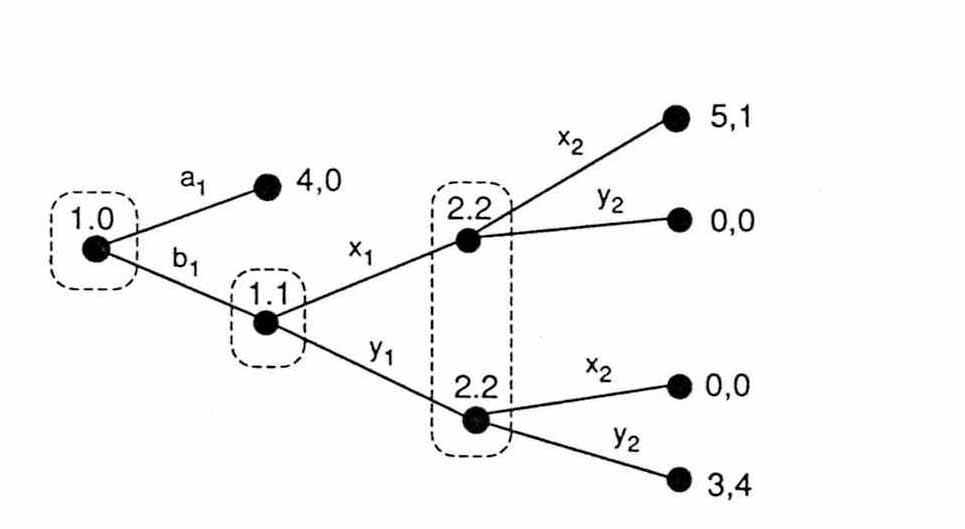
Среди всех равновесий подыгры, начинающейся
в узле 1.1, только одно дает больше, чем
первый игрок имел бы, выбрав
.
Поэтому первый игрок выберет
,
а также
.
Следовательно, второй игрок должен
выбрать
(лучший ответ не
).
Если первый игрок будет предполагать,
что второй игрок будет рассуждать
именно так, то первому игроку действительно
придется выбрать
.
(Рассчитаем, почему
- последовательное равновесие.
Пусть
- вероятность выбора
первым игроком.
- верхний узел 2.2.
- нижний узел 2.2.
;
.
Пусть
-
вероятность выбора
вторым игроком.
,
.
;
;
.
|
|
|
|
|
|
4,0 |
4,0 |
|
|
4,0 |
4,0 |
|
|
5,1 |
0,0 |
|
|
0,0 |
3,4 |
Нормальное представление рассматриваемой игры.
Стратегия 
сильно доминируема.
|
|
|
| ||
|
|
|
|
|
|
|
|
4,4,0 |
4,4,0 |
4,4,0 |
4,4,0 |
|
|
5,5,1 |
0,0,0 |
0,0,0 |
3,3,4 |
Многоагентное представление рассматриваемой игры.
Нет доминируемых стратегий.
Естественные аргументы прямой индукции могут быть несовместимы с естественными аргументами обратной индукции.
Пример.
|
|
| ||
|
|
|
| |
|
|
2,0 |
2,0 |
2,0 |
|
|
2,7 |
9,0 |
0,1 |
|
|
2,7 |
1,0 |
1,8 |
.
.
Сокращенное нормальное представление игры.
Как действует второй игрок в узле 2.2.
Прямая индукция:
- слабо доминируемая стратегия первого
игрока. Поэтому в состоянии 3 первый
игрок выберет
,
если он выбрал
в состоянии 1. Так что второй игрок
выберет
.
Обратная индукцияопределяет
единственное совершенное равновесие
в подыграх
,
в которой второй игрок выбирает
.
|
|
| ||
|
|
|
| |
|
|
2,0 |
2,0 |
2,0 |
|
|
2,7 |
9,0 |
0,1 |
|
|
2,7 |
1,0 |
1,8 |
.
.
Сокращенное нормальное представление игры – пример игры, в которой итеративное удаление слабо доминируемых стратегий может привести к различным результатам, в зависимости от порядка вычеркивания этих стратегий.
Порядок удаления, соответствующий обратной индукции.
Сначала удаляем
.
Получим
|
|
|
|
|
|
2,0 |
2,0 |
|
|
2,7 |
0,1 |
|
|
2,7 |
1,8 |
.
.
Потом
.
Получим
|
|
|
|
|
|
2,0 |
2,0 |
|
|
2,7 |
1,8 |
.
.
Потом
.
Получим
|
|
|
|
|
2,0 |
|
|
1,8 |
.
Потом
:
|
|
|
|
|
2,0 |
.
Осталось равновесие (
,
)
Порядок удаления, соответствующий прямой индукции.
|
|
| ||
|
|
|
| |
|
|
2,0 |
2,0 |
2,0 |
|
|
2,7 |
9,0 |
0,1 |
|
|
2,7 |
1,0 |
1,8 |
.
.
Сначала вычеркиваем
.
Получаем
|
|
| ||
|
|
|
| |
|
|
2,0 |
2,0 |
2,0 |
|
|
2,7 |
9,0 |
0,1 |
.
.
Потом удаляем
.
Получаем
|
|
| |
|
|
| |
|
|
2,0 |
2,0 |
|
|
2,7 |
0,1 |
.
.
Потом удаляем
.
|
|
| |
|
|
| |
|
|
2,0 | |
|
|
2,7 | |
.
.
Осталось два решения: (
,
)
– выигрыш 2,0 и (
,
)
– выигрыш 2,7.