4.6.Совершенные равновесия в подыграх

Большой вклад в разработку этого понятия сделал Selten(1965,1978,1975).

Для любой вершины - множество всех вершин и ветвей, которые следуют за, включая.

Вершина является подкорнем, еслилибо, (- множество всех вершин, в которых игрок находится в информационном состоянииs), либо.

Т.е. если подкорень, то совершающие действия после, знают, что траектория проходила через.

Подыгра игры- игра, которая создается

1) удалением всех ветвей и вершин, не следующих за ,

2) объявлением корнем игры.

Совершенное равновесие в подыграх игры- это равновесие в стратегиях поведения втакое, что для любой подыгры игрыограничение этих стратегий поведения на подыгру является также равновесием в стратегиях поведения в подыгре.

Если является последовательным равновесием в игре, тогдаявляется совершенным равновесием в подыграх игры. Но множество совершенных равновесий в подыграх игрыможет быть больше, чем множество сценариев последовательного равновесия.

Пример.

Мы рассматривали игру

не является совершенным равновесием в подыграх игры, т.к.не является равновесием в подыгре, начинающейся в вершине 2.2.

Пример.

Отличие от предыдущей игры в том, что введен «пустой» третий игрок.

В этой игре нет подыгры (разве что рассматривать конечные вершины как подыгры, состоящие из одного узла), за исключением самой игры .

Поэтому является совершенным равновесием в подыграх этой игры.не является сценарием последовательного равновесия, т.к.не рациональное действие для второго игрока.

Пример.

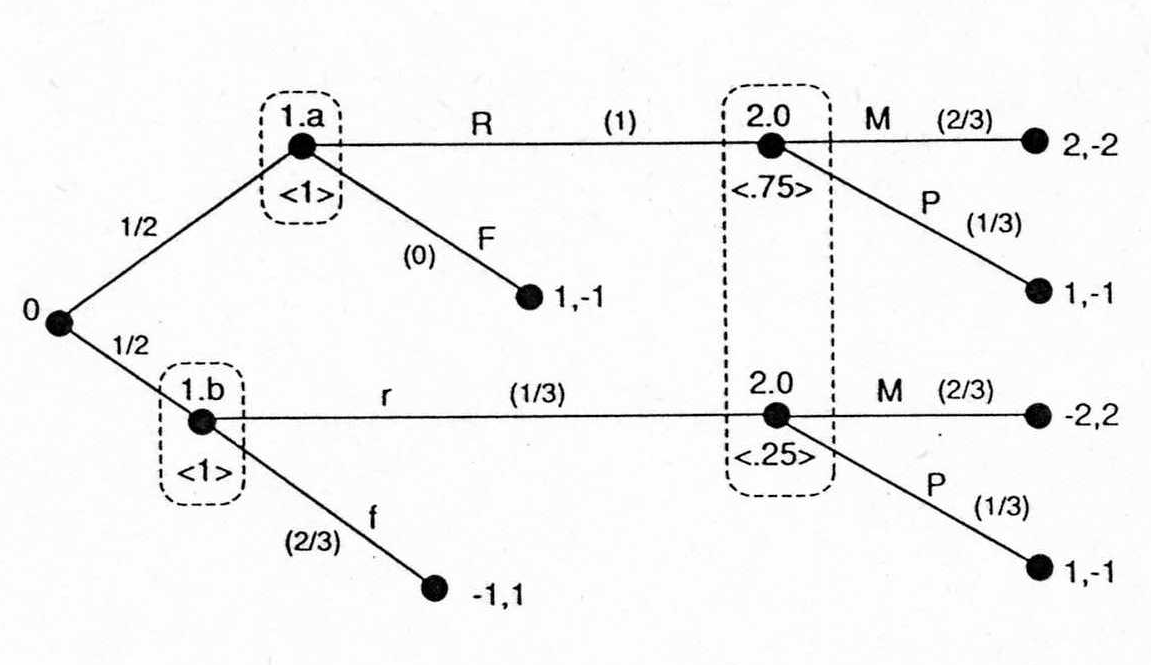
Простая карточная игра

- последовательно рациональный сценарий. Последовательно рациональный сценарий этой игры является совершенным равновесием в подыграх игры, т.к. подыгрой может быть только сама игра.

Часть простой карточной игры. Не является подыгрой , т.к. верхний узел 2.0 не следует за 1.b.

В любом равновесии этой игры первый игрок должен выбирать fс вероятностью 1, т.к. второй игрок выберет 2 с вероятностью 1 (-1<2), а не с вероятностью, как в равновесии всей игры.

4.7.Игра с совершенной информацией

Игра с совершенной информацией – это игра в развернутой форме, в которой каждое информационное состояние каждого игрока приписано только одному узлу, в котором игрок принимает решение, т.е. . В игре с совершенной информацией вектор мнений состоит из единиц. В ней каждый узел является подкорнем. Поэтомукаждое совершенное равновесие в подыграх игры является сценарием последовательного равновесия.

Игры с совершенной информацией моделируют ситуацию, в которой индивидуумы совершают действия поочередно. Двигаясь, игрок знает все про прошлые действия и информированность всех игроков.

Шахматы, шашки – игры с совершенной информацией.

Зададим игру в стратегической форме . Решением Штакельберга вназывается совершенное равновесие в подыграх игры в развернутой форме с совершенной информацией, которое строится по игреследующим образом:

Игрокам из приписывается порядок ходов. Каждый игрокiвыбирает движение изпосле того, как он узнал движения всех игроков, делающих ход раньше него.

Игрок, который ходит первым, называется «лидер по Штакельбергу».

Существуют много решений по Штакельбергу для данной игры в стратегической форме, для каждого способа упорядочивания игроков – свое решение. Как дальше увидим, существует по крайней мере одно решение по Штакельбергу в чистых стратегиях для каждого порядка.

Пример.

	2,1	3,2
	1,4	4,3

Если первый игрок является лидером, то стратегия второго игрока - выбрать, если первый игрок выбрали выбрать, если первый игрок выбрал. Первый игрок выберет, так чторешение – (3,2).

Если второй игрок – лидер, то первый игрок выберет, если второй игрок выберети выберет, если второй выберет. Второму игроку выгодно выбрать, так чторешение игры – (4,3).

Быть лидером – не всегда преимущество, как показано на этом примере (4≥3).

Зададим игру в развернутой форме. По ней можно построить много других игр, которые отличаются от нее выигрышами из,- множество конечных вершин в. Эти игры называются однородными играми. Мы скажем, что некоторое свойство присуще всем однородным играм с совершенной информацией, если для любой игры сс совершенной информациейоткрытое и плотное множество платежных функций из, которое порождает игры, отличающиеся оттолько по выигрышам и которым это свойство присуще .

(Множество плотно в , если каждый вектор изявляется пределом некоторой последовательности векторов из этого множества, синоним – всюду плотное множество).

Теорема4.7.Если- игра в развернутой форме с совершенной информацией, то существует по крайней мере одно последовательное равновесие вв чистых стратегиях. Более того, для всех однородных игр с совершенной информацией существует только одно последовательное равновесие.

Эта теорема гарантирует, что каждый порядок дает по крайней мере одно решение по Штакельбергу в чистых стратегиях.