4.3. Перпендикулярность прямой и плоскости
Из курса элементарной геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости.Но, исходя из теоремы о проецировании прямого угла, перпендикуляр, проведенный к прямым общего положения, на КЧ проецируется с искажением. Поэтому применительно к начертательной геометрии признак перпендикулярности прямой и плоскости формулируется следующим образом.
Признак перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся линиям уровня этой плоскости.
Это связано с тем, что только к линиям уровня на плоскостях проекций можно построить прямой угол без искажения. В качестве линий уровня плоскости, при решении задач на перпендикулярность геометрических объектов, обычно выбирают горизонталь и фронталь.
Возьмем плоскость общего положения
и проведем в ней горизонталь и фронталь.
Затем из точки пересечения линий уровня
плоскости восстановим перпендикулярАК.
На основании теоремы о проецировании прямого угла горизонтальная проекция перпендикуляра к плоскости общего положения на КЧ располагается перпендикулярно горизонтальной проекции горизонтали плоскости, а следовательно, и к ее горизонтальному следу, а фронтальная проекция перпендикуляра – фронтальной проекции фронтали и фронтальному следу.
Рис. 4.6
Пример:Из точки А провести
перпендикуляр к плоскости
и найти его основание.
Рис. 4.7
Частный случай:Прямая перпендикулярна проецирующей плоскости.
В этом случае перпендикулярная прямая будет являться линией уровня и на КЧ перпендикулярными будут вырожденная проекция плоскости (след проекций) и соответствующая проекция прямой.
Рис. 4.8
Пример:Найти расстояние от точки
А до фронтально-проецирующей плоскости
.
Рис. 4.9
4.4. Перпендикулярность плоскостей
Признак перпендикулярности плоскостей:
Плоскость перпендикулярна другой, если она проходит через перпендикуляр к этой плоскости.
Плоскость перпендикулярна другой плоскости, если она перпендикулярна прямой, лежащей в этой плоскости.
Итак, зная, как располагаются проекции прямой, перпендикулярной плоскости, легко строить взаимно-перпендикулярные плоскости. Исходя из признака перпендикулярности плоскостей можно:
построить перпендикуляр к заданной плоскости и через него провести искомую плоскость
или
в заданной плоскости взять прямую и перпендикулярно ей провести искомую плоскость.
В любом из этих случаев задача будет иметь бесчисленное множество решений, если на искомую плоскость не наложены дополнительные условия.
Рассмотрим два примера построения перпендикулярных плоскостей.
Пример:
Через точку
А провести плоскость, перпендикулярную
плоскости
.
Вариант 1:
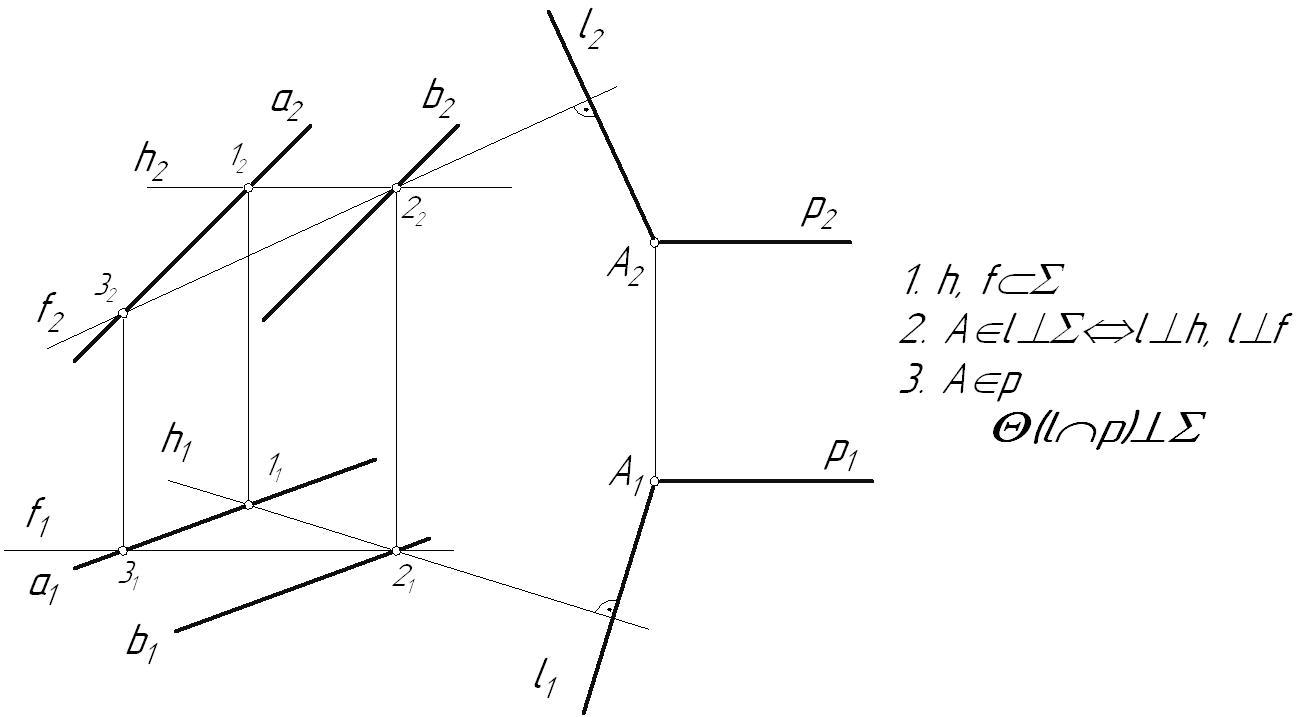
Рис. 4.10
Новая плоскость задана двумя пересекающимися прямыми, одна из которых отвечает условию перпендикулярности плоскостей (прямая l), в зависимости от выбора второй прямой, искомая плоскость может занимать различное положение в пространстве. В данном случае прямая p – профильно-проецирующая, следовательно, сама плоскость является профильно-проецирующей плоскостью.