Assembler / P19

19. Математический сопроцессор 19.1. Плавающие числа

До сих пор мы использовали только целые числа: знаковые и беззнаковые. Можно условиться вставлять в эти числа десятичную точку на фиксированной позиции. Так мы получим числа с фиксированной точкой. Но такой подход нельзя признать удовлетворительным, ведь на практике приходится вести вычисления, в которых одновременно участвуют и очень большие и очень маленькие числа (по абсолютной величине). Для таких вычислений введена система чисел с плавающей точкой (floatingpoint numbers), или просто — плавающих чисел. Прилагательное "плавающий" показывает, что положение десятичной точки не зафиксирована. Для плавающих чисел введен специальный стандарт IEEE 754. Он реализован в изучаемых нами процессорах.

Плавающее число может иметь много эквивалентных представлений. Например,

26.375 2.6375 101 2637.5 10-2 .

Общее представление плавающего числа имеет вид:

Здесь b — основание системы счисления. di — цифры ( 0 di b 1), L e U . Если d0 0 (при x 0 ), то такая плавающая система называется нормализованной. Итак, в

приведенном выше примере из многих представлений только одно ( 2.6375 101 ) является нормализованным. Тогда набор цифр числа f d0 d 1 d t 1 называется мантиссой, e —

порядком (показателем), а t — точностью. Плавающая система определяется четыремя параметрами: b, t, L, U.

Числа, представимые в плавающей системе, расположены на числовой оси неравномерно.

между 16384 и 32768. В процессорах фирмы Intel плавающие числа представлены в трех форматах, носящих условные названия: с одинарной точностью, с двойной точностью, с расширенной точностью. Сначала тщательно изучим формат с одинарной точностью.

Числа с одинарной точностью Представление плавающего числа с одинарной точностью занимает 4 байта, т.е. его длина

составляет 32 бита. Бит 31 отведен для знака числа (0 — положительные, 1 — отрицательные, о представлении плавающего нуля — разговор особый), биты 30:23 — для порядка числа, биты 22:0 — для его мантиссы.

Здесь есть свои особенности.

Основание системы счисления b = 2. Система нормализованная. Поэтому d0 = 1 (если число не является нулем). Но если старшая цифра мантиссы всегда равна 1, зачем ее хранить? За этот счет выигрывается дополнительный разряд мантиссы и увеличивается точность. Старшая цифра двоичного представления носит название "скрытый бит" (hidden bit).

Порядок может быть положительным и отрицательным. Так как на порядок отведены 8 бит, то, как мы уже знаем, e [ 128;127] . В каком формате хранить порядок?

Напрашивается решение: в дополнительном коде. Оказывается, это неудобно, и используется представление со смещением: e e 127 . Это "смещение" по-английски носит название bias (помните, нам ранее встретились два английских термина: offset и displacement, которые переводятся на русский язык словом "смещение"). Тогда –128 переводится в –1 = 11111111, а –127 — в 0 = 00000000. Эти коды будут использованы в

1

особых целях. Поэтому для показателя (порядка) остается диапазон [–126, 127]. Почему выбрано такое странное представление, со смещением? Тогда легко сравнивать плавающие числа на "больше–меньше". Их можно сравнивать, как длинные целые, а это делается очень быстро.

Теперь посмотрим пример представления числа в формате с обычной точностью, но сначала научимся переводить из десятичной в двоичную форму числа от 0 до 1. Для этого

знак = 1, т.к. число отрицательное,

порядок = 1000 0011,

мантисса = 101 0011 0000 0000 0000 0000 (старший бит скрыт!) Окончательно имеем

1100 0001 1101 0011 0000 0000 0000 0000 = C1D30000h.

Проверку правильности вычислений проведем несколькими способами. 1. Программы на языке Си.

Преобразуем указатель на плавающее число к указателю на длинное целое и выведем на экран содержимое.

#include <stdio.h> float p = –26.375; void main()

{printf("%lx\n", *(long*)&p);

}

Воспользуемся конструкцией union.

#include <stdio.h> union {

float p; long f;

} u;

void main()

{u.p = –26.375; printf("%lX\n", u.f);

}

2. Программа на языке Ассемблера. nn.asm

.MODEL small

2

.DATA

DD –26.375 END

Получим листинг этой программы: tasm/l nn.asm

В листинге находим строку C1D30000 DD –26.375. (В файле nn.asm можно было опустить первые две строки, но тогда пришлось бы мириться с сообщением об ошибке)

3. В Turbo Debugger.

В панели данных окна CPU отобразите данные как float, введите –26.375, затем отобразите данные как long.

Задача. Представить вручную число –0.75 в формате с одинарной точностью и проверить правильность перевода описанными выше способами.

19.2. Двойная и расширенная точность.

Формат c одинарной точностью в ряде случаев неприемлем, как мы увидим на примере. Поэтому используются еще два формата: с двойной точностью и с расширенной точностью. Сведем эти форматы в таблицу.

Таблица *.1

DQ расшифровывается как Define Quadword — определить учетверенное слово; DT расшифровывается как Define Ten bytes — определить десять байтов.

Представление с расширенной точностью реализовано в сопроцессоре. Для ускорения вычислений скрытый бит в сопроцессоре не используется.

Задание A7.

Осуществить вручную перевод числа в формат обычной, двойной и расширенной точности и проверьте правильность перевода с помощью листинга программы на языке Ассемблера.

Пример выполнения.

Осуществим перевод числа –26.375.

Сначала переведем число в двоичную нормализованную форму. Абсолютная величина числа равна 26.375.

Двоичное представление целой части: 2610 = 110102.

Вычисление двоичного представления дробной части числа, представим в виде схемы:

Итак, 0.37510 = 0.0112. Проверим: 0.375 1000375 83 0 12 1 14 1 18 .

3

Мы получили, что 26.37510 = 11010.0112. Нормализуем это число. Для этого нужно

переместить десятичную точку влево на четыре позиции. Получим 1.1010011 24 . Последующие вычисления сведем в таблицу

=C03A600000000000. (64 /4 = 16 цифр)

3)Расширенная точность: 1 100000000000011 11010011 = 1100 0000 0000 0011 1101 0011 = C003D300000000000000. (80 /4 = 20 цифр)

Текст программы для проверки flonums.asm

.MODEL small

.DATA

DD –26.375

DQ –26.375

DT –26.375 END

Получение листинга: c:\tasm\bin\tasm /l flonums.asm

Задача. Напишите программу на языке Си, которая выведет 16-ричные коды представления чисел с двойной и расширенной точностью.

Теперь изучим, как получить число из его представления в одном из перечисленных форматов. Пусть sgn — значение знакового бита, f1f2… биты в поле мантиссы, e —

значение в поле порядка. Тогда

одинарная точность (–1)sgn(1.f1f2…f23) 2e–127. двойная точность (–1)sgn(1.f1f2…f52) 2e–1023. расширенная точность (–1)sgn(f1.f2…f64) 2e–16383.

Пример. Представление числа с одинарной точностью имеет вид 101111110110…, т.е. 1| 01111110|110… Тогда sgn = 1, e = 126, f1 = 1, f2 = 1, fk = 0 (k > 2). (–1)1(1.11) 2126–127 =

(–1) 1.75 2–1 = – 0.875.

#include <stdio.h> float a,b,c,t1,t2,t3,d; int main() {

a = 95.0; b = 0.02;

t1 = (a + b) * (a + b);

4

t2 = - 2.0 * a * b - a * a; t3 = b * b;

c = (t1 + t2) / t3;

d = ((a+b)*(a+b)-2.0*a*b-a*a)/(b*b); printf("c = %f d = %f\n",c,d);

return 0;

}

Эта программа вычисляет указанное выражение двумя способами: разбивая его на промежуточные величины t1,t2,t3, помещая результат в c, и сразу вычисляя все выражение, помещая результат в d. Получим:

c = 2.441406 d = 1.000000

Значение c заведомо неверно. Теперь сделаем в программе одно-единственное изменение: заменим тип float на тип double. Тогда

c = 1.000000 d = 1.000000

Дадим объяснение полученным результатам. Как производится сложение плавающих чисел? Сначала надо сделать у них одинаковые порядки. Это можно добиться за счет сдвига мантиссы одного из слагаемых. При равных порядках можно складывать мантиссы. Но при сдвиге мантиссы вправо часть ее разрядов безвозвратно теряется. При работе с короткими мантиссами float это дает существенный эффект. При операциях с длинными мантиссами double эффект потери части младших разрядов становится незаметным.

Почему в первом случае вычисление d дало верный результат? Все вычисления проводились внутри сопроцессора с расширенной точностью, без записи промежуточных результатов вычислений в переменные типа float.

Приведенные результаты получены с использованием компилятора Turbo C. В VC++ вы можете для первого варианта программы получить результат:

c = 1.000000 d = 1.000000

Дело в том, что VC++ проводит оптимизацию кода программы. Он "видит", что переменные t1,t2,t3 более в программе не используются, а значит и выделять для них память нет необходимости. Все промежуточные значения сохраняются в регистрах сопроцессора. Чтобы воспроизвести указанный эффект, надо либо отключить оптимизацию (например, установить для проекта режим Debug, а не Release), либо выводить с помощью printf значения t1,t2,t3.

Вывод. Все расчеты над числами с плавающей точкой надо вести используя тип double, а не float. Окончательные результаты можно сохранять в формате float (например, в файле), если имеются ограничения на размер хранимых данных.

19.4. Специальные численные значения Будем рассматривать эти значения для расширенного формата. К специальным

Здесь вертикальными линиями отделены поля знака, порядка и мантиссы. Для нечисла есть более тонкая классификация: различают "сигнальные" (signal) и "тихие" (quit) нечисла. Но мы не будем подробно изучать этот вопрос (см. [Григорьев 486, т.2]).

Если число представляется в виде x|0…0|x…x (за исключением x|0…0|00…0), то такие числа считаются ненормализованными и исключаются из рассмотрения.

5

В формате с двойной или одинарной точностью, если поля порядка и мантиссы нулевые, то число — положительный или отрицательный нуль. В других случаях надо учитывать скрытый бит.

Приведем программу, в которой выводятся "бесконечности" (для VC++) #include <stdio.h>

union { float f; int i;

} u;

int main() {

u.i = 0x7F800000; printf("%f\n", u.f); u.i = 0xFF800000; printf("%f\n", u.f); return 0;

}

Программа выводит 1.#INF00 и –1.#INF00. Чтобы переделать ее в программу для Turbo C, замените int i на long i. Тогда программа выведет +INF и –INF.

19.5. Математический сопроцессор.

Математический сопроцессор (FPU — Floating Point Unit), специально предназначенный для вычислений с плавающими числами, появился уже для процессора 8086. Сопроцессор был реализован на отдельной микросхеме 8087. Это продолжалось для последующих моделей: для 80286 сопроцессор 80287, для 80386 сопроцессор 80387. В 486-й модели процессор и сопроцессор были объединены на одном кристалле — это сразу увеличило общее быстродействие. Так же было сделано и в последующих моделях.

19.5.1. Регистры сопроцессора

В FPU имеется восемь 80-разрядных регистров: R0, R1,…,R7. В них хранятся плавающие числа с расширенной точностью. Имеются также три 16-битовых регистра:

регистр управления

регистр состояния

регистр тэгов

Есть еще два регистра, указывающие на команду и операнд при возникновении особых случаев. (Мы не будем разбирать их функции.)

Адресация регистров R0, R1,…, R7 необычна. Программист никогда не обращается к регистрам по их именам. В регистре состояния есть поле ST(13:11). Номер регистра R0, R1,…,R7 вычисляется по формуле:

номер регистра = (номер регистра в команде + ST) mod 8.

Пусть например в поле ST хранится число 6. Тогда ссылки на регистры сопроцессора имеют вид, показанный справа на рис.

Рис.

6

Например, команда сложения плавающих чисел fadd st(1),st берет свои операнды из регистров R7 и R6. Если же в ST записано число 7, то операнды будут взяты из R0 и R7. Итак, набор регистров сопроцессора представляет собой "закольцованный стек". Отсюда и название поля ST — первые две буквы слова stack. Такая организация регистров не случайна. Как мы увидим на примере при вычислении арифметического выражения промежуточные результаты помещается в стек. А элементами этого стека являются регистры сопроцессора.

Регистр тэгов описывает содержимое регистров FPU

00 — действительное число, 01 — нуль, 10 — нечисло (бесконечность), 11 — пустой.

19.5.2. Команды Коды команд начинаются с пяти бит 11011. Это информация для ЦП: передать

команду для выполнения в FPU. Ассемблерная мнемоника команд начинается с буквы F (Float).

В системе команд FPU можно выделить несколько групп команд: команды передачи данных, команды сравнения, арифметические команды, команды вычисления трансцендентных функций (логарифма, арктангенса и т.д.). Подробное изучение этих команд не входит в нашу задачу. Арифметические выражения прекрасно транслируют компиляторы языков высокого уровня. Посмотрим работу этих команд на примере

19.5.3. Пример программы для вычисления арифметического выражения.

Программа вычисляет значение квадратного трехчлена 3x 2 7x 2 при x = 2. В обратной польской записи формула принимает вид 3 x * x * 7 x * – 2 +. В процессе вычисления операнды размещаются в стеке регистров сопроцессора.

npol.c float t,x,y; void main()

{x = 2.0;

y = 3*x*x – 7 * x + 2;

}

Обычными командами tcc –v npol.c и td npol.exe мы получаем исполняемый файл с отладочной информацией и загружем его в отладчик. Переменная t введена для удобства отладки.

Закроем окна Module и Watch, откроем окно CPU. Сначала обратимся к панели данных: Alt+F10/ Goto. Вводим адрес 0xA8 (мы узнале его из кода, который будет приведен ниже). Далее Alt+F10/ Display As/ Float. Мы увидим константы, для которых транслятор выделил ячейки памяти

ds:00A8 2 3 ds:00B0 7 0

Уменьшим окно CPU и разместим на экране новое окно: F10/ View/ Numeric Processor.

(описание панелей окна)

С помощью локального меню (Alt+F10) обнулим (Zero) все регистры FPU и сделаем их пустыми (Empty). Вы должны получить

7

fld (Float load) считывает операнд, преобразует его в формат с раширенной точностью, осуществляет декркмент ST на 1 по модулю 8ю, операнд помещается в вершину стека. Результат fld

fstp (Float store with pop) считывает содержимое регистра ST(0), после необходимого преобразования результат записывается в операнде, происходит инкремент ST по модулю 8 (это и означает выталкивание — pop).

Число 2 превратилось в "мусор", потому что регистр помечен как пустой. В результате этих двух команд в ячейке x записано число 2.0.

Теперь изучим, как проходит вычисление по формуле. (самостоятельно прослеживайте содержимое стека)

Проведите изучение этой программы в VC++ (теперь переменную t можно удалить). В окне Watch выводите содержимое регистров st0, st1, st2. При этом можно использовать спецификатор формата x, чтобы посмотреть 16-ричное содержимое регистра или ячейки памяти.

Задача. Получите в VC++ ассемблерный код этой программы. Превратите его в программу на языке Ассемблера, использующую малую модель памяти, а также секции данных и кода. Изучите работу этой программы в Turbo Debugger.

8

return 0;

}

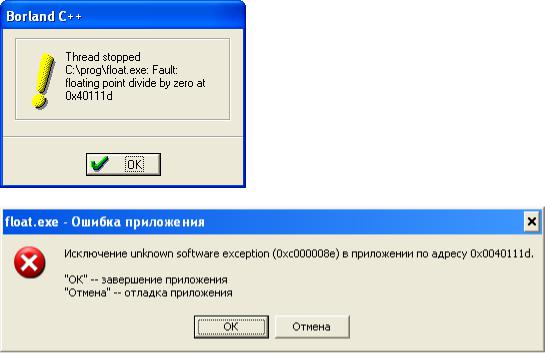
Если делать в 32-разрядной среде, то сообщения

А в 16-разрядной:

Floating point error: Divide by 0. Abnormal program termination

Получим ассемблерный файл bcc –S res.c

и отредактируем его (удалим много лишнего и добавим привычные директивы).

.MODEL small

.286

.STACK 100h

.DATA r1 DD 1.0 r2 DD 0.0

rDD ?

.CODE

start: mov ax, @data mov ds, ax

9

fstp dword ptr r mov ax, 4C00h int 21h

END start

В отладчике

#float#start: start: mov ax, @data

10